1.1平方根的概念
图片预览




文档简介
课件14张PPT。x2=2x =之 平方根的概念 12.1 平方根与立方根义务教育课程标准试验教科书
七年级 上册华东师范大学出版社 教学目的:
1.知识与技能:通过动手操作,使学生地一步感受到无理数在实际生活中的大量存在,形成认识,会根号表示平方根。
2.过程与方法:在活动中感知无理数产生的实际背景和学习的必要性,了解平方根的概念。
3.情感态度与价值观:提高学生的应用意识,发展学生的数感,体会无理数的应用价值。
重点、难点、关键:
1.重点:平方根的概念及求某些数的平方根的方法;
2.难点:平方根的概念、算术平方根的概念;
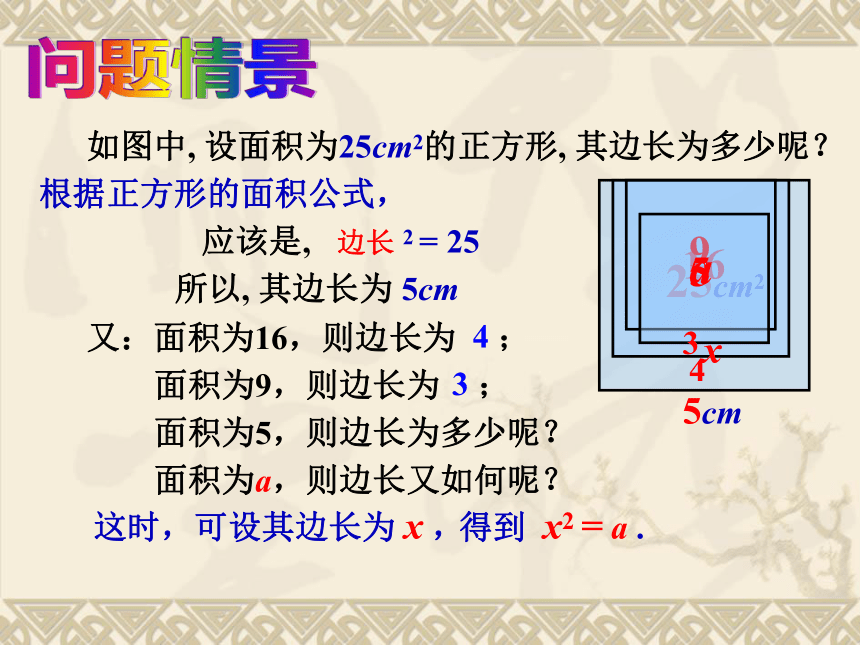
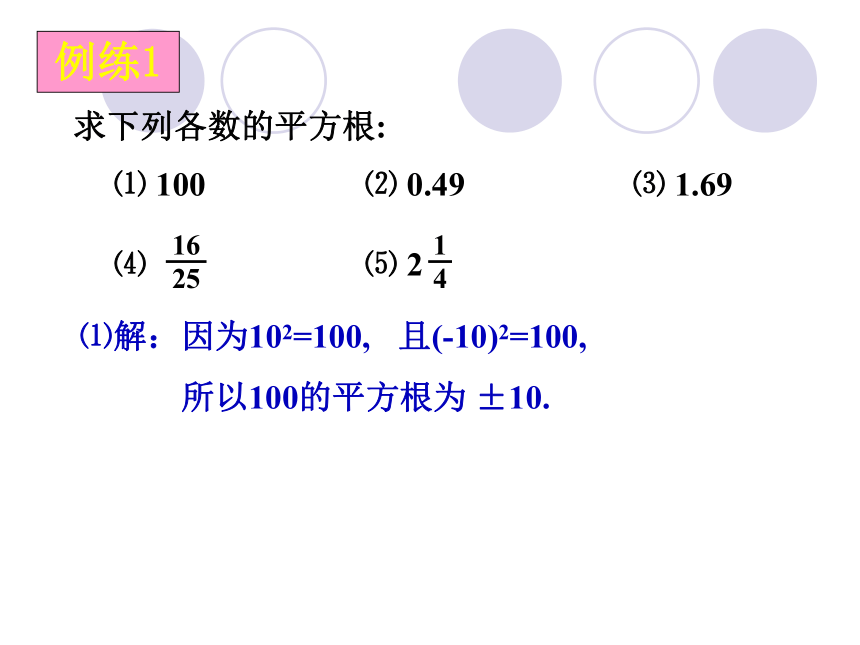
3. 关键:从实际出发应用平方的思想进行逆向思考。如图中, 设面积为25cm2的正方形, 其边长为多少呢? 5cm问题情景x应该是, 2 = 25 又:面积为16,则边长为 4 ; a5边长所以, 其边长为 5cm 4 面积为9,则边长为 3 ; 3 面积为5,则边长为多少呢? 面积为a,则边长又如何呢? 根据正方形的面积公式, 这时,可设其边长为 x , 得到 x2 = a . 新知概念如果一个数 x 的平方等于 a, 那么这个数 x 叫做 a 的平方根. 就是说, 当 x2 =a 时, 称 x 是 a 的平方根. (a≥0)例练1求下列各数的平方根: ⑴ 100 ⑵ 0.49 ⑶ 1.69
⑷ ⑸ 2 ⑴解:因为102=100,且(-10)2=100,所以100的平方根为 ±10.下列各数的平方根会是怎样的? ⑴ 121 ⑵ 232 ⑶ (-4)2
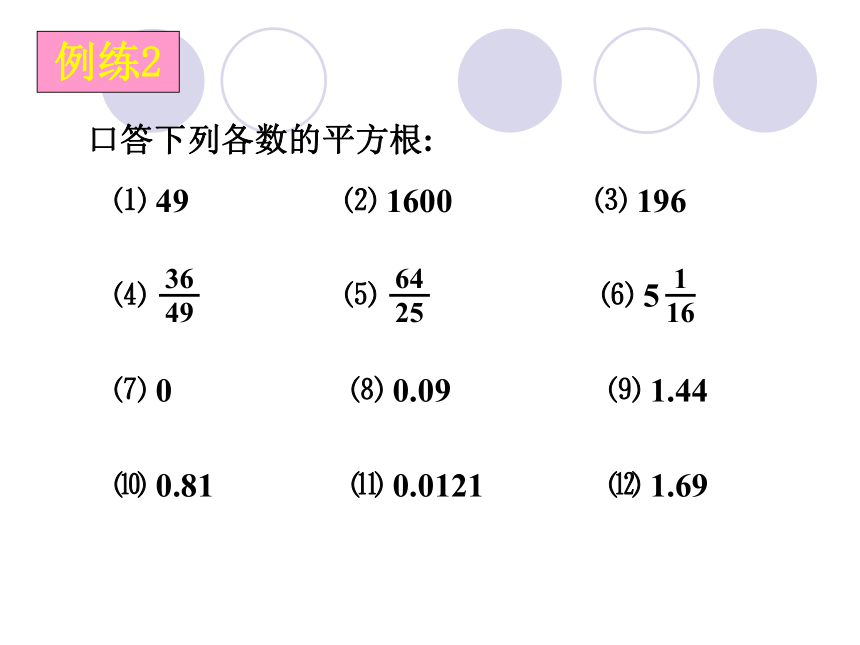
⑷ 0 ⑸ -25 平方根的情况:⑴一个正数的平方根有两个,它们是互为相反数; ⑵ 0的平方根只有一个, 想一想 就是它本身0; ⑶负数没有平方根. 例练2口答下列各数的平方根: ⑴ 49 ⑵ 1600 ⑶ 196 ⑺ 0 ⑻ 0.09 ⑼ 1.44 ⑽ 0.81 ⑾ 0.0121 ⑿ 1.69 辨一辨 下列叙述正确的打“ √” ,错误的打“×”:⑴ 16的平方根是 ±4; ( ) √⑵ ±7是49的平方根 ; ( ) √⑶ 112的平方根是11; ( ) ×⑷ -9是81的平方根; ( ) √⑸ 52的平方根是±25; ( ) ×⑹ -9的平方根是 -3; ( ) ×⑺ 0的平方根是 0; ( ) √⑻ 有一个平方根为 -2的数是 -4; ( ) ×⑼ 只有一个平方根的数是0; ( ) √回顾小结1、平方根的概念:当x2=a(a≥0) 时, 就称x是a的平方根.2、相关概念:而a称为x的平方数.即平方根是利用平方数来说的. 任何数都有平方数, 且只有一个; 都有平方根, 根, 3、求一个非负数的平方根的运算叫做开平方.但并不是任何数只有非负数才有平方根, 负数没有平方且正数的平方根是互为相反数的两个数.例练31. 下列表述正确的是( )A. 9的平方根是-3 B. -7是-49的平方根C. -15是225的平方根 D. (-4)2的平方根是-4CD√√√√B±8 36 ±9 思维拓展求下列各式中的x: 1. x2=16 2. 64x2=25 3. (x-1)2=9 x=±4 x=± x-1=±3 x=4 或x= -2 课后作业
课本P6的习题12.1的第1题
板书设计一、平方根的概念
二、平方根的求法
三、平方根的情况七、课后反思
本节课学生新学了平方根,学生对此比较容易理解,但又较易混淆,多强调平方根的个数。
1.知识与技能:通过动手操作,使学生地一步感受到无理数在实际生活中的大量存在,形成认识,会根号表示平方根。
2.过程与方法:在活动中感知无理数产生的实际背景和学习的必要性,了解平方根的概念。
3.情感态度与价值观:提高学生的应用意识,发展学生的数感,体会无理数的应用价值。
重点、难点、关键:
1.重点:平方根的概念及求某些数的平方根的方法;
2.难点:平方根的概念、算术平方根的概念;
3. 关键:从实际出发应用平方的思想进行逆向思考。如图中, 设面积为25cm2的正方形, 其边长为多少呢? 5cm问题情景x应该是, 2 = 25 又:面积为16,则边长为 4 ; a5边长所以, 其边长为 5cm 4 面积为9,则边长为 3 ; 3 面积为5,则边长为多少呢? 面积为a,则边长又如何呢? 根据正方形的面积公式, 这时,可设其边长为 x , 得到 x2 = a . 新知概念如果一个数 x 的平方等于 a, 那么这个数 x 叫做 a 的平方根. 就是说, 当 x2 =a 时, 称 x 是 a 的平方根. (a≥0)例练1求下列各数的平方根: ⑴ 100 ⑵ 0.49 ⑶ 1.69
⑷ ⑸ 2 ⑴解:因为102=100,且(-10)2=100,所以100的平方根为 ±10.下列各数的平方根会是怎样的? ⑴ 121 ⑵ 232 ⑶ (-4)2
⑷ 0 ⑸ -25 平方根的情况:⑴一个正数的平方根有两个,它们是互为相反数; ⑵ 0的平方根只有一个, 想一想 就是它本身0; ⑶负数没有平方根. 例练2口答下列各数的平方根: ⑴ 49 ⑵ 1600 ⑶ 196 ⑺ 0 ⑻ 0.09 ⑼ 1.44 ⑽ 0.81 ⑾ 0.0121 ⑿ 1.69 辨一辨 下列叙述正确的打“ √” ,错误的打“×”:⑴ 16的平方根是 ±4; ( ) √⑵ ±7是49的平方根 ; ( ) √⑶ 112的平方根是11; ( ) ×⑷ -9是81的平方根; ( ) √⑸ 52的平方根是±25; ( ) ×⑹ -9的平方根是 -3; ( ) ×⑺ 0的平方根是 0; ( ) √⑻ 有一个平方根为 -2的数是 -4; ( ) ×⑼ 只有一个平方根的数是0; ( ) √回顾小结1、平方根的概念:当x2=a(a≥0) 时, 就称x是a的平方根.2、相关概念:而a称为x的平方数.即平方根是利用平方数来说的. 任何数都有平方数, 且只有一个; 都有平方根, 根, 3、求一个非负数的平方根的运算叫做开平方.但并不是任何数只有非负数才有平方根, 负数没有平方且正数的平方根是互为相反数的两个数.例练31. 下列表述正确的是( )A. 9的平方根是-3 B. -7是-49的平方根C. -15是225的平方根 D. (-4)2的平方根是-4CD√√√√B±8 36 ±9 思维拓展求下列各式中的x: 1. x2=16 2. 64x2=25 3. (x-1)2=9 x=±4 x=± x-1=±3 x=4 或x= -2 课后作业
课本P6的习题12.1的第1题
板书设计一、平方根的概念
二、平方根的求法
三、平方根的情况七、课后反思
本节课学生新学了平方根,学生对此比较容易理解,但又较易混淆,多强调平方根的个数。
