4.1 正弦和余弦（4）

课件20张PPT。4.1 正弦和余弦第4课时 正弦和余弦综合湖南省新邵县酿溪中学王军旗1、巩固锐角的正弦、余弦定义及熟练掌握特殊角的正弦、余弦值。
2、进一步掌握正弦余弦之间的关系。
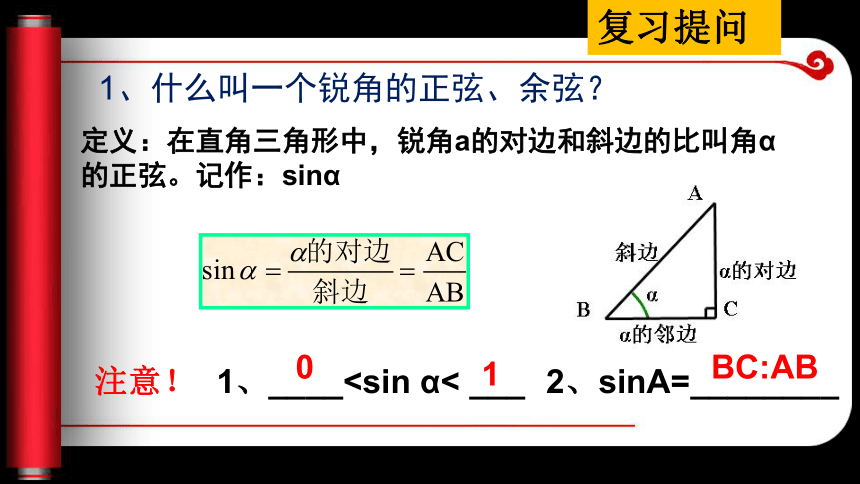
3、能够综合运用正弦、余弦定义解决简单问题。 学习目标定义：在直角三角形中，锐角a的对边和斜边的比叫角α的正弦。记作：sinα注意！1、____1、什么叫一个锐角的正弦、余弦？定义：在直角三角形中，锐角a的邻边和斜边的比叫角α的余弦。记作：cosα cosα= :1、__2、cos B=
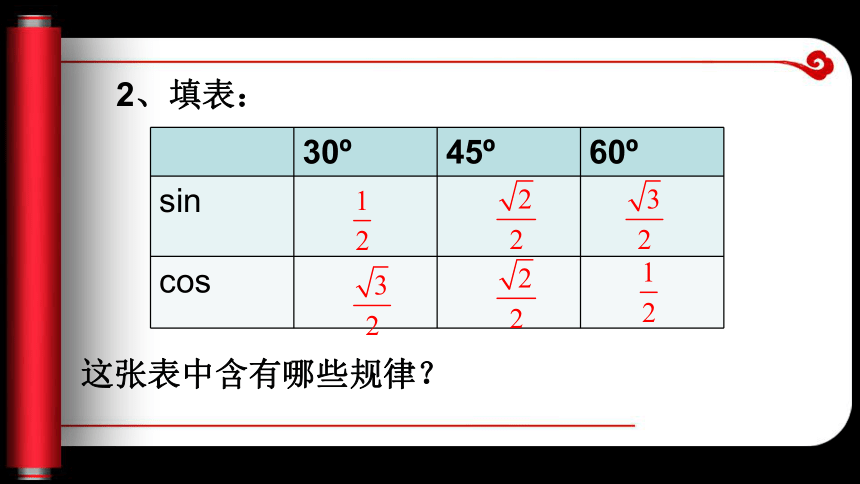
_____01注意！2、填表：这张表中含有哪些规律？用式子表示为：Rt△ABC中：∠C=90o
sinA=cosB, sosA=sinB
或者：sinα=cos(90 o-α),cosα=sin(90 o-α)
(α为锐角） 如果两个角互余，那么其中一个角的正弦等于另一个角的余弦，一个角的余弦等于另一个角的正弦。3、互为余角的两个角正弦值和余弦值有什么关系？解(1)按键顺序：第一步：开机，按“ON/C”第二步：设置输入状态。如果屏幕上没有显示“DEG”就 按“DRG”直到屏幕上显示“DEG”第三步：依次按“sin”,“0”“D’M’S”,“45”，“D’M’S”，“36”，“D’M’S”,“=”显示：0.01324、（1）用计算器求：sin 45 ′ 36 ″(精确到0.0001）
（2）已知cos α=0.2345，则α=____(精确到1 ′）
（2）按键顺序：“2ndf”,“cos”, “0.2345”,“=”，“D’M’S”显示：76o26′1、已知锐角的正弦或余弦值求这个角要用到“D’M’S”.
2、已知锐角的正弦或余弦值求这个角时，要用“D’M’S”把结果化为“度、分、秒”的形式。注意！计算：（1）sin230 o+cos230 o , （2）cos245 o+cos245 o 解：（1） sin230 o+cos230 o=主题讲解主题一、同一锐角的正弦值和余弦值的关系
（2）cos245 o+cos245 o =由此你有什么猜想？猜想：对于任意锐角α都有：sin2α+cos2α=1这是为什么呢？如图，Rt △ABC中， ∠C=90, ∠A、 ∠B、 ∠C的对边分别是：a,b,c 例1、在Rt△ABC中，若∠C=90o,cosA= 求sinA解法1、利用正弦函数定义计算：
设AC=12k,AB=13k.
BC=
∴sinA=解法2、例1、在Rt△ABC中，若∠C=90o,cosA= 求sinA例2、已知△ABC中，∠C=90o，sinA= ，a =2,求cosA,b,c的值。【分析】利用sin2α+cos2α=1求cosA.
利用sinA=a:c,求c，利用cosA=b:c
求b，或勾股定理求b.解：已知：△ABC中，∠C=90o，a:b=2:3,求∠A的正弦和余弦值。解:设a=2k,b=3k,则变式练习例3、已知等腰三角形ABC中，AB=AC=10,BC=12,求sinB,cosB的值解：作AD ⊥BC于D, ∵AB=AC,
∴BD=DC= ?BC=6.
∴
∴sinB=
主题二、正弦和余弦的实际运用D例4、（2010浙江宁波） 如图，某河道要建造一座公路桥，要求桥面离地面高度AC为3米，引桥的坡角∠ABC为15°，则引桥的水平距离BC的长是 米(精确到0.1米) .?解：【分析】先用∠ABC的正弦求出AB,再用∠ABC的余弦求BC.或勾股定理求BC1.在等腰三角形ABC中，AB=AC=10,BC=12,求cos 解：作AD ⊥BC于D, ∵AB=AC,
∴BD=DC= ?BC=6, ∠BAD= ? ∠A
∴D变式练习2、（2010 广东汕头）如图，已知Rt△ABC中，斜边BC上的高AD＝4，cosB＝ 则AC＝_________．解：5小结
1、回顾正弦与余弦的定义。
2、回顾同角的正弦与余弦的关系。
3、回顾互为余角的两个角的正弦、余弦的关系。
作业 P 108 6,7,8