第三章图形与证明（二）复习教案

图形与证明（二）（1）
总 课时 第 16 课时
教学目标：
1、 探索并掌握等腰三角形和等边三角形的性质定理和判定定理的证明；
2、 掌握直角三角形全等的判定定理；
3、 掌握平行四边形和特殊的平行四边形（矩形、菱形、正方形）的性质定理和判定定理；
4、 能够应用上述定理证明简单的几何问题。
教学重点：
1、 探索并掌握等腰三角形和等边三角形的性质定理和判定定理的证明；
2、 掌握直角三角形全等的判定定理；
3、 掌握平行四边形和特殊的平行四边形（矩形、菱形、正方形）的性质定理和判定定理；
教学难点： 能够应用上述定理证明简单的几何问题。
一、知识回顾：
1、 你能用网络图表示本章的知识吗？试一试。
2、（2005·四川）用两个全等的直角三角形一定能拼出的图形是 （ ）
A、等腰梯形 B、直角梯形 C、菱形 D、矩形
3、若等腰三角形的一个角是，那么它的另外两个角分别为 。
若它的一边长为6，周长为，则的取值范围是 。
二、探索活动：
㈠自学相信自己
1、底角为，腰长为的等腰三角形的面积为 。
2、直线两两相交（不交于一点），那么到三条直线距离相等的点有 个。
3、已知菱形的边长为2，，对角线、相交于点，则 ，菱形的面积= 。
㈡思索、交流
1、已知：矩形中，延长到，使，是的中点，求证：。
2、如图所示，在正方形中，、相交于点，、分别在对角线、上，且。
（1） 求证：；
（2） 对上述命题，若点在的延长线上，点在的延长线上，其余条件不变，那么结论 “”是否成立？若成立，请在图（2）中画出图形，并给出证明过程；若不成立，请说明理由
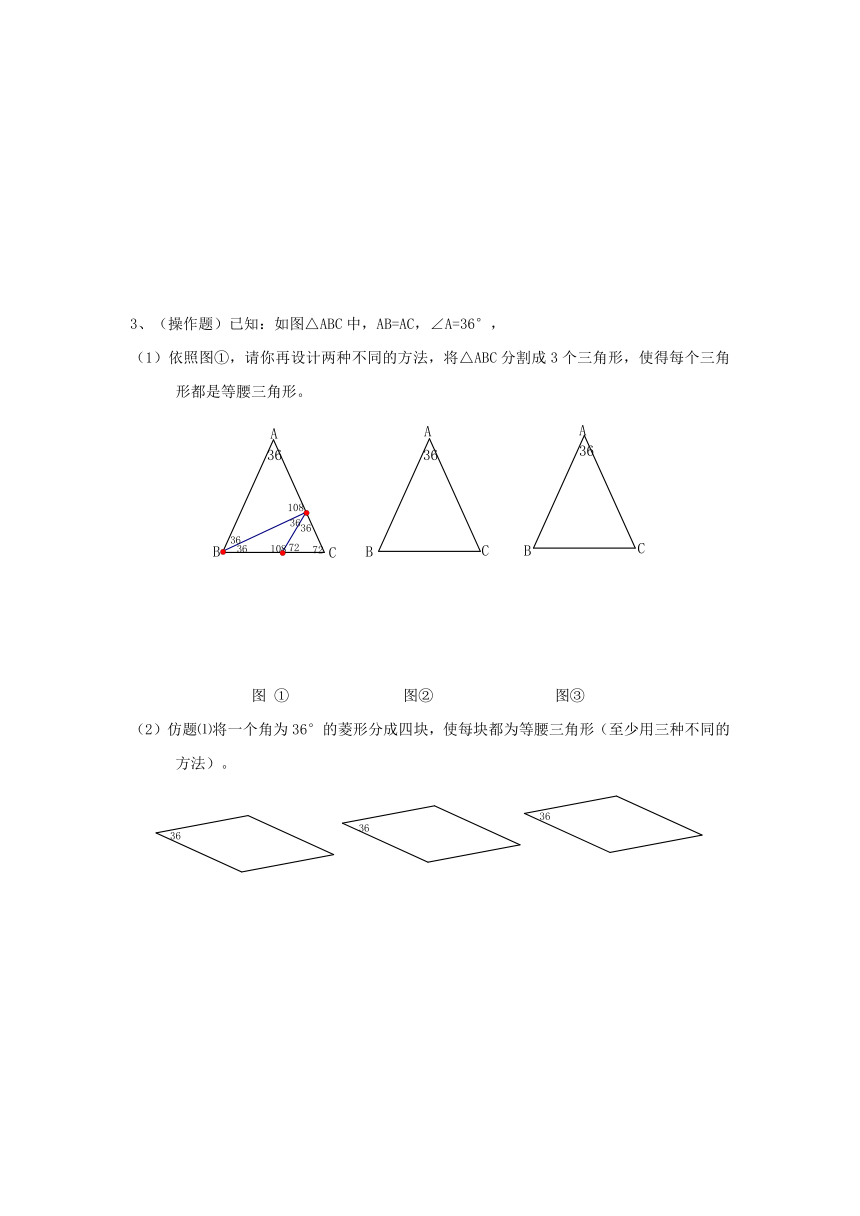
3、（操作题）已知：如图△ABC中，AB=AC，∠A=36°，
（1）依照图①，请你再设计两种不同的方法，将△ABC分割成3个三角形，使得每个三角形都是等腰三角形。
图 ① 图② 图③
（2）仿题⑴将一个角为36°的菱形分成四块，使每块都为等腰三角形（至少用三种不同的方法）。
三、体会与交流
课题：图形与证明复习（2）
总 课时 第 17 课时
一．知识点：
1．根据“等腰三角形，等腰梯形的性质定理与判定定理，直角三角形全等的判定定理，角平分线的性质定理与判定定理，三角形中位线定理等。”填表：
图形名称 图形 性质（符号语言） 判定（符号语言） 典型结论或例题
等腰三角形
等腰梯形
角平分线
线段的垂直平分线
三角形中位线 [来源:21世纪教育网]
梯形中位线 [来源:21世纪教育网]
平行四边形
矩形
菱形
正方形21世纪教育网
直角三角形全等的判定方法有： 。2．通过相关问题进一步体会探究过程中所运用的类比，对比，转化等数学思想方法。
二．基础练习：
1．平行四边形ABCD中，如果∠A=55°，那么∠C的度数是
(A)45° (B)55° (C)125° (D)145°
2． 如图1，在△ABC中，D、E分别是AB、AC的中点，BC=12，则DE的长是 (A)4 (B)5 (C)6 (D)7
3．阳光中学阅览室在装修过程中，准备用边长相等的正方形和正三角形两种地砖镶嵌地面，在每个顶点的周围正方形、正三角形地砖的块数可以分别是
A、2，2 B、2，3 C、1，2 D、2，1
4．如图，梯形ABCD中，AD∥BC，∠C＝90°，且AB=AD，连结BD，过A点作BD的垂线，交BC于E。如果EC=3cm，CD=4cm，那么，梯形ABCD的面积是 cm2。
三．典型例题：
1．如图5，在矩形ABCD中，点E是BC上一点，AE=AD，DF⊥AE，垂足为F。线段DF与图中的哪一条线段相等？先将你猜想出的结论填写在下面的横线上，然后再加以证明。
即DF= 。(写出一条线段即可)
证明：
2．已知：将一副三角板(Rt△ABC和Rt△DEF)如图①摆放，点E、A、D、
B在一条直线上，且D是AB的中点。将Rt△DEF绕点D顺时针方向旋转角α(0°＜α＜90°)，在旋转过程中，直线DE、AC相交于点M，直线DF、BC相交于点N，分别过点M、N作直线AB的垂线，垂足为G、H。
（1）当α＝30°时(如图②)，求证：AG=DH；
（2）当α＝60°时(如图③)，(1)中的结论是否成立？请写出你的结论，并说明理由；
（3）当0°＜α＜90°时，(1)中的结论是否成立？请写出你的结论，并根据图④说明理由。
四．巩固练习
1．如图，已知等腰梯形中，，，，则此等腰梯形的周长为（　　）Ａ． 19 Ｂ．20 Ｃ．21 Ｄ．22
2．将五边形纸片ABCDE按如图方式折叠，折痕为AF，点E、D分别落在 E’、 D’，已知∠CFD’等于 A、31° B、28° C、24° D、22°
[来源:21世纪教育网]
3．如图，在矩形ABCD中，对角线AC、BD相交于点G，E为AD的中点，连接BE交AC于点F，连接FD，若∠BFA=90°，则下列四对三角形：①△BEA与△ACD；②△ FED与△DEB；③△CFD与△ABC；④△ADF与△CFB。其中相似的为
A、①④ B、①② C、②③④ D、①②③
4．在下图的正方形网格中有一个直角梯形ABCD，请你在该图中分别按下列要求画出图形（不要求写出画法）：
（1） 把直角梯形ABCD向下平移3个单位得到直角梯形A1B1C1D1；
（2） 将直角梯形ABCD绕点D逆时针旋
（3） 转180°后得到直角梯形A2B2C2D
5．如图所示，在平面直角坐标中，四边形OABC是等腰梯形，BC∥OA，OA=7，AB=4，∠ COA=60°，点P为x轴上的—个动点，点P不与点0、点A重合．连结CP，过点P作PD交AB于点D．
(1)求点B的坐标；
(2)当点P运动什么位置时，△OCP为等腰三角形，求这时点P的坐标；
(3)当点P运动什么位置时，使得∠CPD=∠OAB，且=，求这时点P的坐标。
6．如图，在△ABC中，AB=AC=1，点D,E在直线BC上运动．设BD=x, CE=y.
(l）如果∠BAC=300，∠DAE=l050，试确定y与x之间的函数关系式；
(2）如果∠BAC=α,∠DAE=β,当α, β满足怎样的关系时，(l）中y与x之间的函数关系式还成立？试说明理由．
21世纪教育网
7．如图，在Rt△ABC中，∠C＝90°，AC＝12，BC＝16，动点P从点A出发沿AC边向点C以每秒3个单位长的速度运动，动点Q从点C出发沿CB边向点B以每秒4个单位长的速度运动．P，Q分别从点A，C同时出发，当其中一点到达端点时，另一点也随之停止运动．在运动过程中，△PCQ关于直线PQ对称的图形是△PDQ．设运动时间为t（秒）．（1）设四边形PCQD的面积为y，求y与t的函数关系式；（2）t为何值时，四边形PQBA是梯形？（3）是否存在时刻t，使得PD∥AB？若存在，求出t的值；若不存在，请说明理由；（4）通过观察、画图或折纸等方法，猜想是否存在时刻t，使得PD⊥AB？若存在，请估计t的值在括号中的哪个时间段内（0≤t≤1；1＜t≤2；2＜t≤3；3＜t≤4）；若不存在，请简要说明理由．
E
A
B
D
C
E
第4题图
45°
60°
A
E
D
B
C
F
A
G
D
H
M
E
F
C
B
(N)
第2题图
图①
图②
A
B
C
D
F
G
E
第3图
E
D
F
D’
E’
A
B
C
第2图
A
D
B
C
第1
A
P
C
Q
B
D