(苏科版九年级上)数学:3.1等腰三角形的性质和判定课件1
文档属性
| 名称 | (苏科版九年级上)数学:3.1等腰三角形的性质和判定课件1 |

|
|
| 格式 | rar | ||
| 文件大小 | 1003.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-11-01 00:00:00 | ||
图片预览





文档简介
课件14张PPT。3.1等腰三角形的性质和判定1、什么叫做等腰三角形?
2、等腰三角形有哪些性质?
3、上述性质你是怎么得到的?你能否用从基本事实出发,对它们进行证明?知识回顾 等腰三角形的两个底角相等.
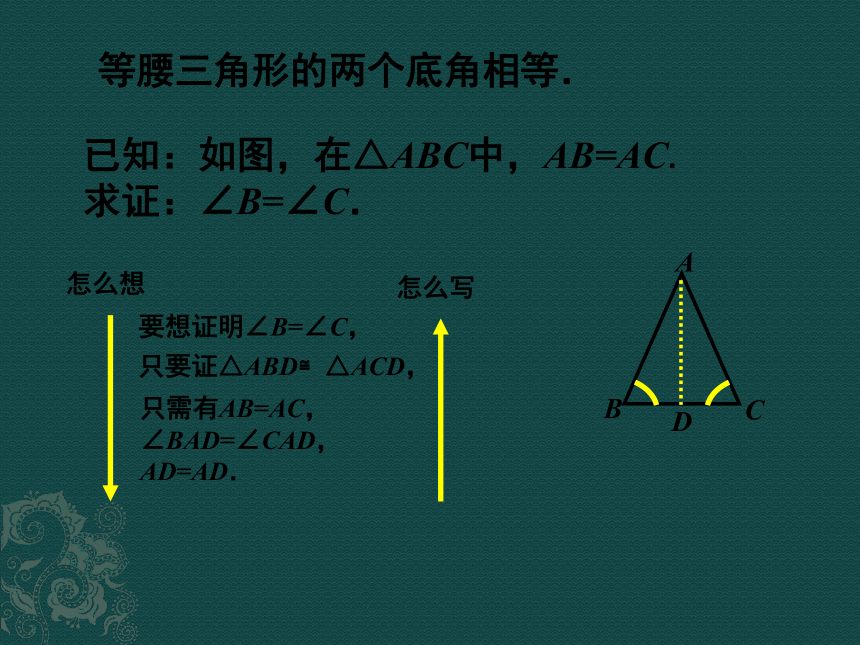
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合. 等腰三角形的两个底角相等. 已知:如图,在△ABC中,AB=AC.
求证:∠B=∠C.要想证明∠B=∠C,只需有AB=AC,
∠BAD=∠CAD,
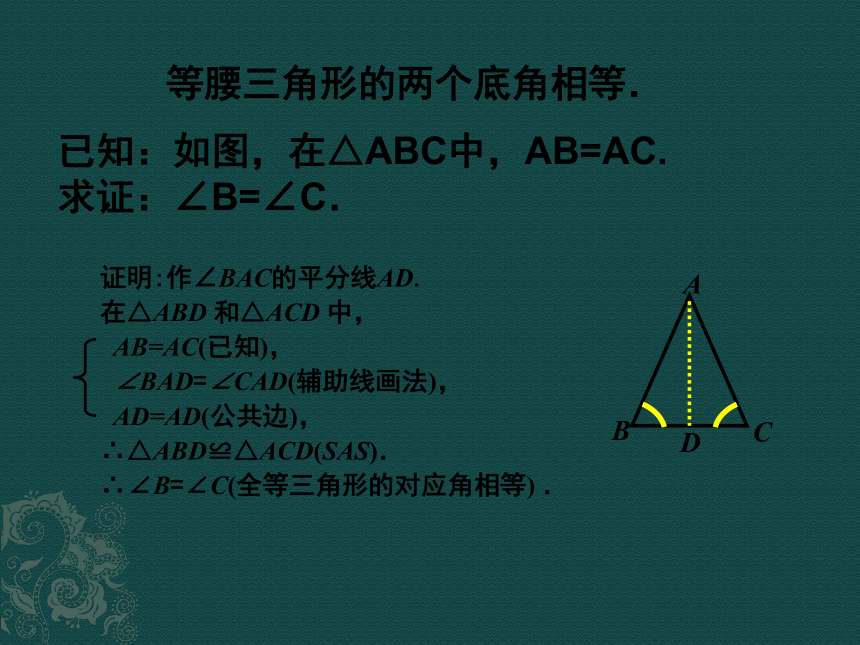
AD=AD.只要证△ABD≌△ACD, 等腰三角形的两个底角相等. 已知:如图,在△ABC中,AB=AC.
求证:∠B=∠C.证明:作∠BAC的平分线AD.
在△ABD 和△ACD 中,
AB=AC(已知),
∠BAD=∠CAD(辅助线画法),
AD=AD(公共边),
∴△ABD≌△ACD(SAS).
∴∠B=∠C(全等三角形的对应角相等) . 等腰三角形的两个底角相等. 定理 定理 等腰三角形的顶角平分线、底边
上的中线、底边上的高互相重合. (简称“等边对等角”)已知:如图,在△ABC中,∠B=∠C.
求证:AB=AC. 逆命题 如果一个三角形的两个角相等,那么这两个角所对的边也相等.定理 等腰三角形的两个底角相等. 如果一个三角形的两个角相等,
那么这两个角所对的边也相等.已知:如图,在△ABC中,∠B=∠C.
求证:AB=AC.逆命题定理 (简称“等角
对等边”)要想证明AB =AC,
只需证∠B=∠C.
已知∠EAD=∠DAC,
只需证∠EAD =∠B,
∠DAC =∠C. 已知:∠EAC是△ABC的外角,
AD平分∠EAC,且 AD∥BC.
求证:AB=AC.例题 已知:∠EAC是△ABC的外角,
AD平分∠EAC,且 AD∥BC.
求证:AB=AC.例题证明:∵AD∥BC,
∴∠EAD=∠B,
∠DAC=∠C.
∵∠EAD =∠DAC,
∴∠B=∠C.
∴ AB=AC (等角对等边).拓展
已知:∠EAC是△ABC的外角,
,且 AD∥BC.
求证: AD平分∠EAC AB=AC 证明:∵AD∥BC,
∴∠EAD=∠B,
∠DAC=∠C.
∵AB=AC,
∴∠B=∠C.
∴∠EAD=∠DAC.
即 AD平分∠EAC...例2 证明:到一条线段两个端点距离相等的点在这条线段的垂直平分线上。 巩固练习: 1、证明:线段垂直平分线上的点到这条线段两个端点距离相等。 2、如图,BO平分∠CBA, CO平分∠ABC, 且MN//BC,设AB=12,BC=24,AC=18,求△AMN的周长。学有所获证明思路
(怎么想)证明过程
(怎么写)逆过来等腰三角形的性质定理和判定定理证明思路(作辅助线的方法)
2、等腰三角形有哪些性质?
3、上述性质你是怎么得到的?你能否用从基本事实出发,对它们进行证明?知识回顾 等腰三角形的两个底角相等.
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合. 等腰三角形的两个底角相等. 已知:如图,在△ABC中,AB=AC.
求证:∠B=∠C.要想证明∠B=∠C,只需有AB=AC,
∠BAD=∠CAD,
AD=AD.只要证△ABD≌△ACD, 等腰三角形的两个底角相等. 已知:如图,在△ABC中,AB=AC.
求证:∠B=∠C.证明:作∠BAC的平分线AD.
在△ABD 和△ACD 中,
AB=AC(已知),
∠BAD=∠CAD(辅助线画法),
AD=AD(公共边),
∴△ABD≌△ACD(SAS).
∴∠B=∠C(全等三角形的对应角相等) . 等腰三角形的两个底角相等. 定理 定理 等腰三角形的顶角平分线、底边
上的中线、底边上的高互相重合. (简称“等边对等角”)已知:如图,在△ABC中,∠B=∠C.
求证:AB=AC. 逆命题 如果一个三角形的两个角相等,那么这两个角所对的边也相等.定理 等腰三角形的两个底角相等. 如果一个三角形的两个角相等,
那么这两个角所对的边也相等.已知:如图,在△ABC中,∠B=∠C.
求证:AB=AC.逆命题定理 (简称“等角
对等边”)要想证明AB =AC,
只需证∠B=∠C.
已知∠EAD=∠DAC,
只需证∠EAD =∠B,
∠DAC =∠C. 已知:∠EAC是△ABC的外角,
AD平分∠EAC,且 AD∥BC.
求证:AB=AC.例题 已知:∠EAC是△ABC的外角,
AD平分∠EAC,且 AD∥BC.
求证:AB=AC.例题证明:∵AD∥BC,
∴∠EAD=∠B,
∠DAC=∠C.
∵∠EAD =∠DAC,
∴∠B=∠C.
∴ AB=AC (等角对等边).拓展
已知:∠EAC是△ABC的外角,
,且 AD∥BC.
求证: AD平分∠EAC AB=AC 证明:∵AD∥BC,
∴∠EAD=∠B,
∠DAC=∠C.
∵AB=AC,
∴∠B=∠C.
∴∠EAD=∠DAC.
即 AD平分∠EAC...例2 证明:到一条线段两个端点距离相等的点在这条线段的垂直平分线上。 巩固练习: 1、证明:线段垂直平分线上的点到这条线段两个端点距离相等。 2、如图,BO平分∠CBA, CO平分∠ABC, 且MN//BC,设AB=12,BC=24,AC=18,求△AMN的周长。学有所获证明思路
(怎么想)证明过程
(怎么写)逆过来等腰三角形的性质定理和判定定理证明思路(作辅助线的方法)
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
