(苏科版九年级上)数学:3.3.4正方形的性质课件
文档属性
| 名称 | (苏科版九年级上)数学:3.3.4正方形的性质课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-11-01 00:00:00 | ||
图片预览





文档简介
课件15张PPT。 苏科版九年级上第一章 图形与证明(二)3.3.4 正方形的性质知识回顾有一组邻边相等,有一个角是直角的平行四边形叫做正方形。
正方形既是矩形又是菱形,它都有什么性质呢?
(1)边的性质: 正方形的四条边都相等 ;
(2)角的性质: 正方形的四个角都是直角 ;
(3)对角线的性质: 正方形的对角线互相垂直平分,并且每条对角线平分一组对角 ;
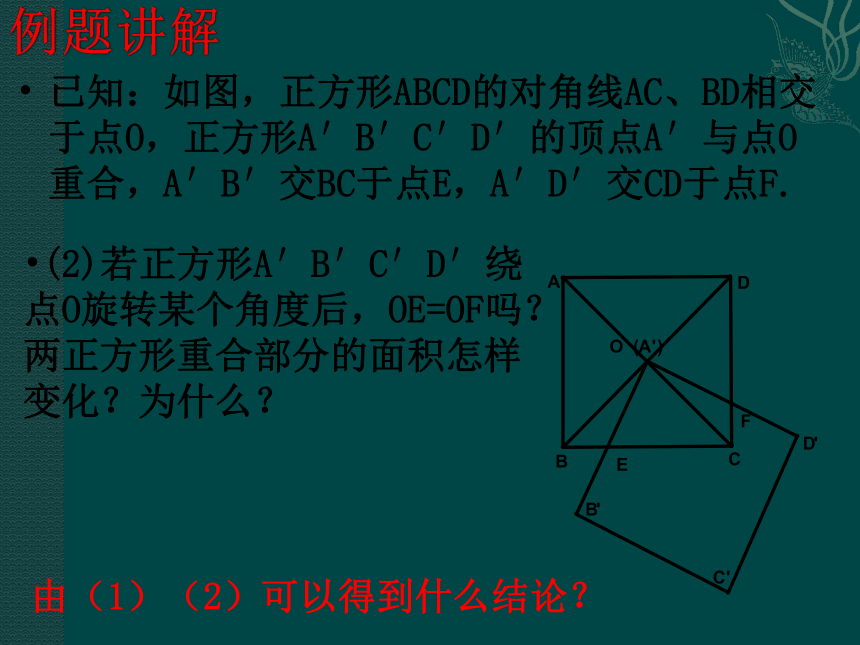
(4)对称性:轴对称、中心对称 .例题讲解 例1、已知:如图,正方形ABCD的对角线AC、BD相交于点O,正方形A′B′C′D′的顶点A′与点O重合,A′B′交BC于点E,A′D′交CD于点F.
(1) E是BC的中点,求证:OE=OF.已知:如图,正方形ABCD的对角线AC、BD相交于点O,正方形A′B′C′D′的顶点A′与点O重合,A′B′交BC于点E,A′D′交CD于点F.(2)若正方形A′B′C′D′绕点O旋转某个角度后,OE=OF吗?两正方形重合部分的面积怎样变化?为什么?
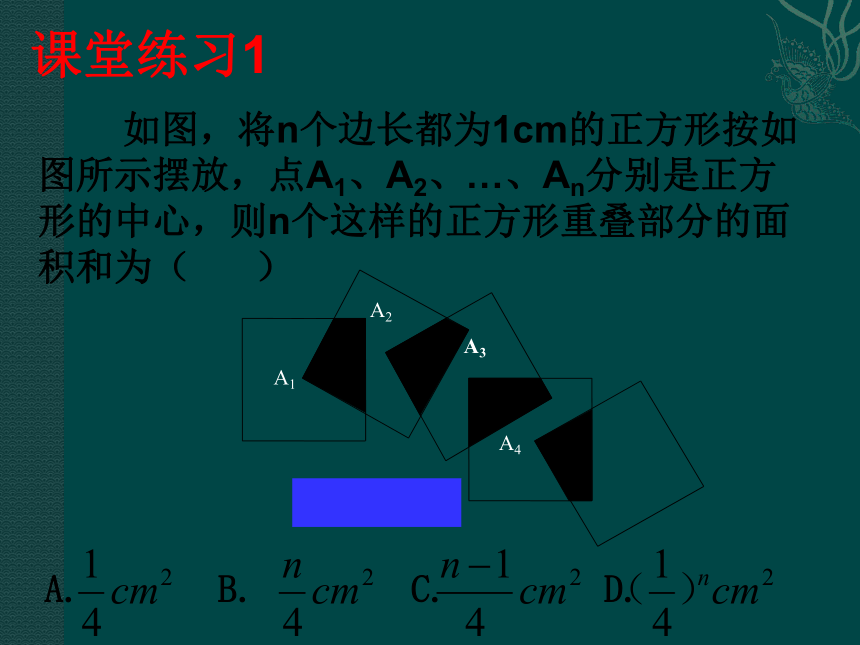
例题讲解 由(1)(2)可以得到什么结论? 如图,将n个边长都为1cm的正方形按如图所示摆放,点A1、A2、…、An分别是正方形的中心,则n个这样的正方形重叠部分的面积和为( )课堂练习1 B. C. D.例2、已知:如图,在正方形ABCD中,E是BC的中点,点F在CD,∠FAE=∠BAE.
求证:AF=BC+EC.已知:如图,在正方形ABCD中,E是BC的中点,点F在CD上,∠FAE=∠BAE.
求证:AF=BC+EC.已知:如图,在正方形ABCD中,E是BC的中点,点F在CD上,∠FAE=∠BAE.
求证:AF=BC+EC.1.求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形. 课堂练习22.在正方形ABCD中:(1)已知:如图①,点E、F分别在BC、CD上,且AE⊥BF,垂足为M,求证:AE=BF.
课堂练习2在正方形ABCD中:(2)如图②,如果点E、F、G分别在BC、CD、DA上,且GE⊥BF,垂足M,那么GE与BF相等吗?证明你的结论.
在正方形ABCD中:(3)如图③,如果点E、F、G、H分别在BC、CD、DA、AB上,且GE⊥HF,垂足M,那么GE与HF相等吗?证明你的结论.
课堂小结正方形与矩形,菱形,平行四边形的关系 :①正方形对边平行.
②正方形四边相等.
③正方形四个角都是直角.
④正方形既是轴对称图形,又是中心对称图形.
⑤正方形对角线相等,互相垂直平分,每条对角线平分一组对.正方形的性质:本节课我们把探索和解决问题的思路、方法、结论,从特殊情形逐步推广到一般的情形,从而得到一般的结论,这也是我们获得数学结论的一种重要的思想方法.
正方形既是矩形又是菱形,它都有什么性质呢?
(1)边的性质: 正方形的四条边都相等 ;
(2)角的性质: 正方形的四个角都是直角 ;
(3)对角线的性质: 正方形的对角线互相垂直平分,并且每条对角线平分一组对角 ;
(4)对称性:轴对称、中心对称 .例题讲解 例1、已知:如图,正方形ABCD的对角线AC、BD相交于点O,正方形A′B′C′D′的顶点A′与点O重合,A′B′交BC于点E,A′D′交CD于点F.
(1) E是BC的中点,求证:OE=OF.已知:如图,正方形ABCD的对角线AC、BD相交于点O,正方形A′B′C′D′的顶点A′与点O重合,A′B′交BC于点E,A′D′交CD于点F.(2)若正方形A′B′C′D′绕点O旋转某个角度后,OE=OF吗?两正方形重合部分的面积怎样变化?为什么?
例题讲解 由(1)(2)可以得到什么结论? 如图,将n个边长都为1cm的正方形按如图所示摆放,点A1、A2、…、An分别是正方形的中心,则n个这样的正方形重叠部分的面积和为( )课堂练习1 B. C. D.例2、已知:如图,在正方形ABCD中,E是BC的中点,点F在CD,∠FAE=∠BAE.
求证:AF=BC+EC.已知:如图,在正方形ABCD中,E是BC的中点,点F在CD上,∠FAE=∠BAE.
求证:AF=BC+EC.已知:如图,在正方形ABCD中,E是BC的中点,点F在CD上,∠FAE=∠BAE.
求证:AF=BC+EC.1.求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形. 课堂练习22.在正方形ABCD中:(1)已知:如图①,点E、F分别在BC、CD上,且AE⊥BF,垂足为M,求证:AE=BF.
课堂练习2在正方形ABCD中:(2)如图②,如果点E、F、G分别在BC、CD、DA上,且GE⊥BF,垂足M,那么GE与BF相等吗?证明你的结论.
在正方形ABCD中:(3)如图③,如果点E、F、G、H分别在BC、CD、DA、AB上,且GE⊥HF,垂足M,那么GE与HF相等吗?证明你的结论.
课堂小结正方形与矩形,菱形,平行四边形的关系 :①正方形对边平行.
②正方形四边相等.
③正方形四个角都是直角.
④正方形既是轴对称图形,又是中心对称图形.
⑤正方形对角线相等,互相垂直平分,每条对角线平分一组对.正方形的性质:本节课我们把探索和解决问题的思路、方法、结论,从特殊情形逐步推广到一般的情形,从而得到一般的结论,这也是我们获得数学结论的一种重要的思想方法.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
