【数学】1.1.6《棱柱、棱锥、棱台和球的表面积》课件(人教b版必修2)
文档属性
| 名称 | 【数学】1.1.6《棱柱、棱锥、棱台和球的表面积》课件(人教b版必修2) |  | |
| 格式 | rar | ||
| 文件大小 | 153.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-11-04 19:01:00 | ||
图片预览







文档简介
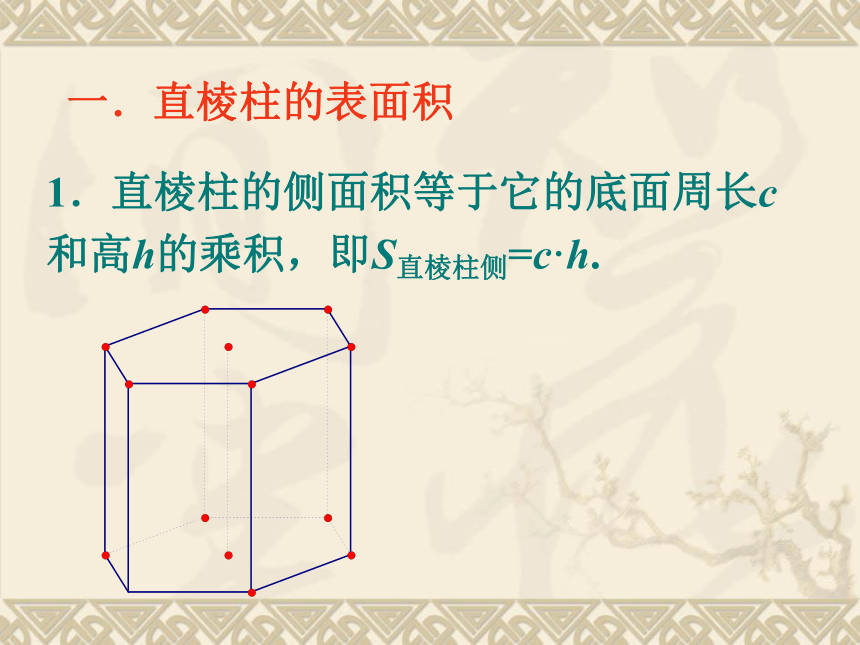
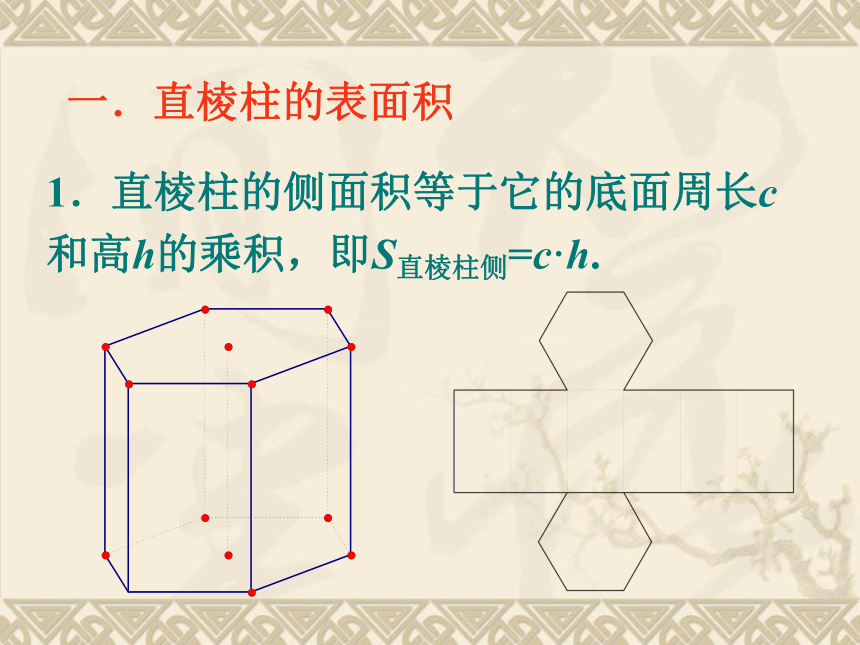
课件31张PPT。1.1.6棱柱、棱锥、棱台和球的表面积 一.直棱柱的表面积 1.直棱柱的侧面积等于它的底面周长c和高h的乘积,即S直棱柱侧=c·h.一.直棱柱的表面积 1.直棱柱的侧面积等于它的底面周长c和高h的乘积,即S直棱柱侧=c·h.2. 直棱柱的表面积就等于侧面积与上、下底面面积的和. 3.斜棱柱的侧面积,可以先求出每个侧面的面积,然后求和,也可以用直截面周长与侧棱长的乘积来求. 其中直截面就是和棱垂直的截面.
如果斜棱柱的侧棱长为l,直截面的周长为c’,则其侧面积的计算公式就是
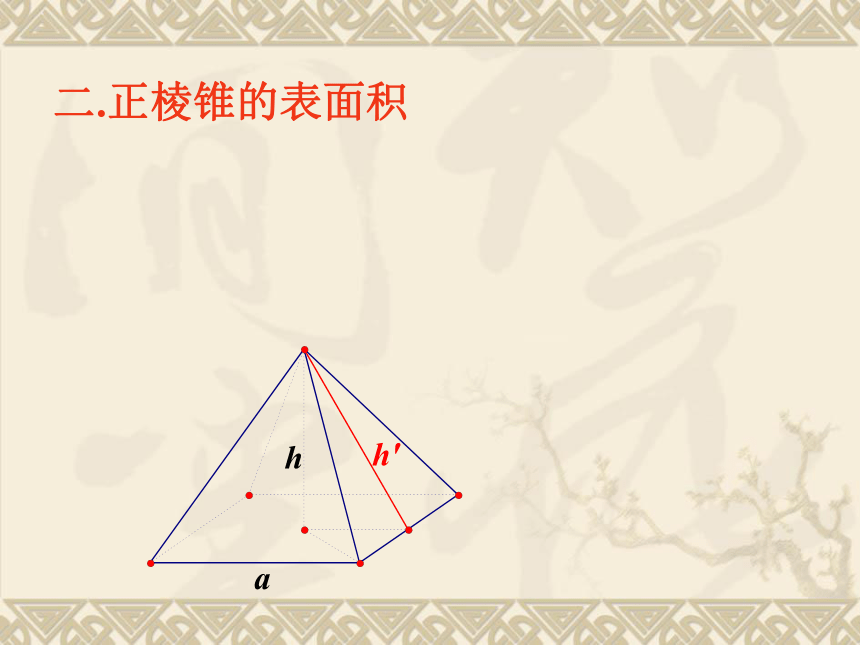
S侧=c’·l.二.正棱锥的表面积 1. 正棱锥的侧面积等于它的底面周长和斜高乘积的一半,即S正棱锥侧= na·h’. 其中a为底面正多边形的边长,底面周长为c,斜高为h’, 二.正棱锥的表面积 二.正棱锥的表面积 1. 正棱锥的侧面积等于它的底面周长和斜高乘积的一半,即S正棱锥侧= na·h’. 其中a为底面正多边形的边长,底面周长为c,斜高为h’, 2.正棱锥的表面积等于正棱锥的侧面积与底面积之和. 如上图,以正四棱锥为例简单推导计算公式。由于正四棱锥的侧面展开图是一些全等的等腰三角形,底面是正多边形,若设它的底面边长为a,底面周长为4a,斜高为h’,容易得到正四棱锥的侧面积计算公式为S正四棱锥侧= ·4a·h’= ch’,
对于正n棱锥,其侧面积计算公式为
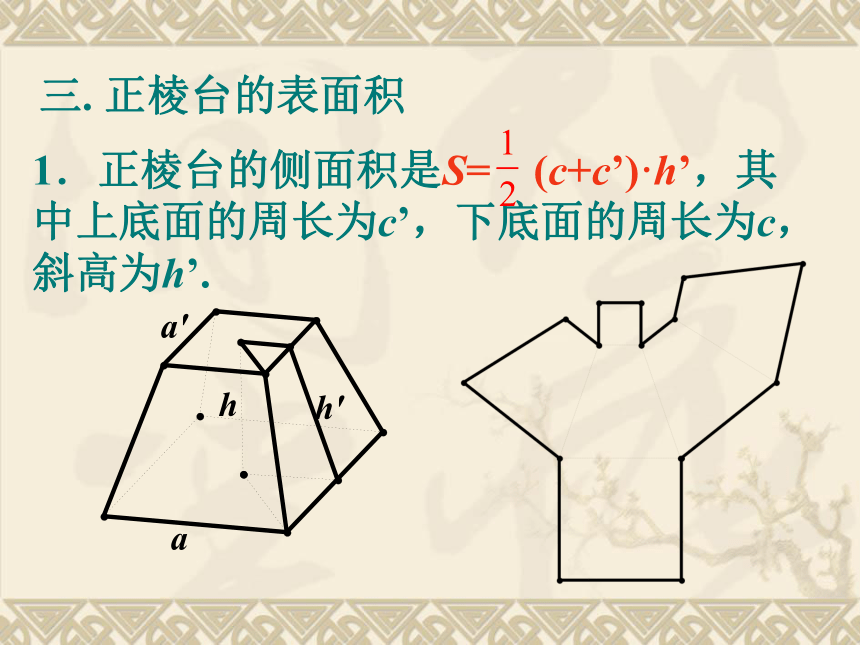
S正棱锥侧= c·h’.三. 正棱台的表面积 1.正棱台的侧面积是S= (c+c’)·h’,其中上底面的周长为c’,下底面的周长为c,斜高为h’. 三. 正棱台的表面积 1.正棱台的侧面积是S= (c+c’)·h’,其中上底面的周长为c’,下底面的周长为c,斜高为h’. 2.正棱台可以看作是用平行正棱锥底面的平面截得的,因此正棱台的侧面展开图是一些等腰梯形,3.正棱台的表面积等于它的侧面积与底面积之和。 设正棱台上、下底面周长为c’,c,斜高为h’,可得正棱台的侧面积
S正棱台侧= (c+c’)·h’。四. 圆柱、圆锥、圆台的侧面积 (1)将圆柱沿一条母线剪开后,展开图是一个矩形,这个矩形的一边为母线,另一边为圆柱底面圆的圆周长,设圆柱底面半径为r,母线长为l,则侧面积
S圆柱侧=2πrl.(2)将圆锥沿一条母线剪开,展开在一个平面上,其展开图是一个扇形,扇形的半径为圆锥的母线,扇形的弧是圆锥底面圆的圆周,因此该扇形的圆心角 θ= ,r为圆锥底面半径,l为圆锥的母线长,根据扇形面积公式可得:S圆锥侧= ·2πr·l=πrl,其中l为圆锥母线长,r为底面圆半径。(3)圆台可以看成是用一个平行底面的平面截圆锥所得,因此圆台的侧面展开图是一个扇环,设圆台上、下底半径为r、R,母线长为l,则S圆台侧=π(r+R)l= (c1+c2)l,其中r,R分别为上、下底面圆半径,c1,c2分别为上、下底面圆周长,l为圆台的母线。 五.球的表面积 球面面积(也就是球的表面积)等于它的大圆面积的4倍,
即S球=4πR2,其中R为球的半径.例1. 一个长方体的长、宽、高分别为5、4、3,求它的表面积。解:长方体的表面积
S=2(5×4+4×3+5×3)=94.例2. 已知正四棱锥底面正方形长为4cm,高与斜高的夹角为30°,求正四棱锥的侧面积及全面积.(单位:cm2,精确到0.01 )解:正棱锥的高PO,斜高PE,底面边心距OE组成直角三角形。 因为OE=2,∠OPE=30°,所以斜高因此S侧= ch’=32(cm2)S全=S侧+S底=48(cm2)例3. 如图所示是一个容器的盖子,它是用一个正四棱台和一个球焊接而成的。球的半径为R,正四棱台的两底面边长分别为3R和2.5R,斜高为0.6R;
(1)求这个容器盖子的表面积;
(2)若R=2cm,为盖子涂色时所用的涂料每0.4kg可以涂1m2,计算100个这样的盖子涂色需涂料多少千克(精确到0.1kg)。S正四棱台=4× ×(2.5R+3R)×0.6R
+(2.5R)2+(3R)2
=21.85R2.S球=4πR2. 因此,这个盖子的全面积为S全=(21.85+4π)R2.解:(1)因为(2)取R=2,π=3.14,得
S全=137.67cm2.又 (137.67×100)÷10000×0.4≈0.6(kg),因此涂100个这样的盖子共需涂料0.6kg.例4. 在球心同侧有相距9cm的两个平行截面,它们的面积分别为49πcm2和400π cm2,求球的表面积.解:由截面圆的面积分别是49πcm2和400π cm2,解得AO1=20cm,
BO2=7cm.
设OO1=x, 则OO2=x+9.所以R2=x2+202=(x+9)2+72.解得x=15(cm).所以圆的半径R=25(cm).所以S球=4πR2=2500π(cm2)练习题:1. 将一个边长为a的正方体,切成27个全等的小正方体,则表面积增加了( )
(A)6a2 (B)12a2
(C)18a2 (D)24a2B2. 在正方体的八个顶点中,有四个恰好是正四面体的顶点,则正方体的表面积与此正四面体的表面积的比值为( )
(A) (B)
(C) (D)B 3. 侧面都是直角三角形的正三棱锥,底面边长为a,该三棱锥的全面积是( )
(A) (B)
(C) (D)A4. 球内接正方体的表面积与球的表面积的比为( )
(A)2:π (B)3:π
(C)4:π (D)6:πA5. 已知正六棱台的上、下底面边长分别是2 和4,高是2,则这个棱台的侧面积等于 。
如果斜棱柱的侧棱长为l,直截面的周长为c’,则其侧面积的计算公式就是
S侧=c’·l.二.正棱锥的表面积 1. 正棱锥的侧面积等于它的底面周长和斜高乘积的一半,即S正棱锥侧= na·h’. 其中a为底面正多边形的边长,底面周长为c,斜高为h’, 二.正棱锥的表面积 二.正棱锥的表面积 1. 正棱锥的侧面积等于它的底面周长和斜高乘积的一半,即S正棱锥侧= na·h’. 其中a为底面正多边形的边长,底面周长为c,斜高为h’, 2.正棱锥的表面积等于正棱锥的侧面积与底面积之和. 如上图,以正四棱锥为例简单推导计算公式。由于正四棱锥的侧面展开图是一些全等的等腰三角形,底面是正多边形,若设它的底面边长为a,底面周长为4a,斜高为h’,容易得到正四棱锥的侧面积计算公式为S正四棱锥侧= ·4a·h’= ch’,
对于正n棱锥,其侧面积计算公式为
S正棱锥侧= c·h’.三. 正棱台的表面积 1.正棱台的侧面积是S= (c+c’)·h’,其中上底面的周长为c’,下底面的周长为c,斜高为h’. 三. 正棱台的表面积 1.正棱台的侧面积是S= (c+c’)·h’,其中上底面的周长为c’,下底面的周长为c,斜高为h’. 2.正棱台可以看作是用平行正棱锥底面的平面截得的,因此正棱台的侧面展开图是一些等腰梯形,3.正棱台的表面积等于它的侧面积与底面积之和。 设正棱台上、下底面周长为c’,c,斜高为h’,可得正棱台的侧面积
S正棱台侧= (c+c’)·h’。四. 圆柱、圆锥、圆台的侧面积 (1)将圆柱沿一条母线剪开后,展开图是一个矩形,这个矩形的一边为母线,另一边为圆柱底面圆的圆周长,设圆柱底面半径为r,母线长为l,则侧面积
S圆柱侧=2πrl.(2)将圆锥沿一条母线剪开,展开在一个平面上,其展开图是一个扇形,扇形的半径为圆锥的母线,扇形的弧是圆锥底面圆的圆周,因此该扇形的圆心角 θ= ,r为圆锥底面半径,l为圆锥的母线长,根据扇形面积公式可得:S圆锥侧= ·2πr·l=πrl,其中l为圆锥母线长,r为底面圆半径。(3)圆台可以看成是用一个平行底面的平面截圆锥所得,因此圆台的侧面展开图是一个扇环,设圆台上、下底半径为r、R,母线长为l,则S圆台侧=π(r+R)l= (c1+c2)l,其中r,R分别为上、下底面圆半径,c1,c2分别为上、下底面圆周长,l为圆台的母线。 五.球的表面积 球面面积(也就是球的表面积)等于它的大圆面积的4倍,
即S球=4πR2,其中R为球的半径.例1. 一个长方体的长、宽、高分别为5、4、3,求它的表面积。解:长方体的表面积
S=2(5×4+4×3+5×3)=94.例2. 已知正四棱锥底面正方形长为4cm,高与斜高的夹角为30°,求正四棱锥的侧面积及全面积.(单位:cm2,精确到0.01 )解:正棱锥的高PO,斜高PE,底面边心距OE组成直角三角形。 因为OE=2,∠OPE=30°,所以斜高因此S侧= ch’=32(cm2)S全=S侧+S底=48(cm2)例3. 如图所示是一个容器的盖子,它是用一个正四棱台和一个球焊接而成的。球的半径为R,正四棱台的两底面边长分别为3R和2.5R,斜高为0.6R;
(1)求这个容器盖子的表面积;
(2)若R=2cm,为盖子涂色时所用的涂料每0.4kg可以涂1m2,计算100个这样的盖子涂色需涂料多少千克(精确到0.1kg)。S正四棱台=4× ×(2.5R+3R)×0.6R
+(2.5R)2+(3R)2
=21.85R2.S球=4πR2. 因此,这个盖子的全面积为S全=(21.85+4π)R2.解:(1)因为(2)取R=2,π=3.14,得
S全=137.67cm2.又 (137.67×100)÷10000×0.4≈0.6(kg),因此涂100个这样的盖子共需涂料0.6kg.例4. 在球心同侧有相距9cm的两个平行截面,它们的面积分别为49πcm2和400π cm2,求球的表面积.解:由截面圆的面积分别是49πcm2和400π cm2,解得AO1=20cm,
BO2=7cm.
设OO1=x, 则OO2=x+9.所以R2=x2+202=(x+9)2+72.解得x=15(cm).所以圆的半径R=25(cm).所以S球=4πR2=2500π(cm2)练习题:1. 将一个边长为a的正方体,切成27个全等的小正方体,则表面积增加了( )
(A)6a2 (B)12a2
(C)18a2 (D)24a2B2. 在正方体的八个顶点中,有四个恰好是正四面体的顶点,则正方体的表面积与此正四面体的表面积的比值为( )
(A) (B)
(C) (D)B 3. 侧面都是直角三角形的正三棱锥,底面边长为a,该三棱锥的全面积是( )
(A) (B)
(C) (D)A4. 球内接正方体的表面积与球的表面积的比为( )
(A)2:π (B)3:π
(C)4:π (D)6:πA5. 已知正六棱台的上、下底面边长分别是2 和4,高是2,则这个棱台的侧面积等于 。
