【数学】1.2.2《空间中的平行关系(2)》课件(人教b版必修2)
文档属性
| 名称 | 【数学】1.2.2《空间中的平行关系(2)》课件(人教b版必修2) |

|
|
| 格式 | rar | ||
| 文件大小 | 207.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-11-04 19:01:00 | ||
图片预览







文档简介
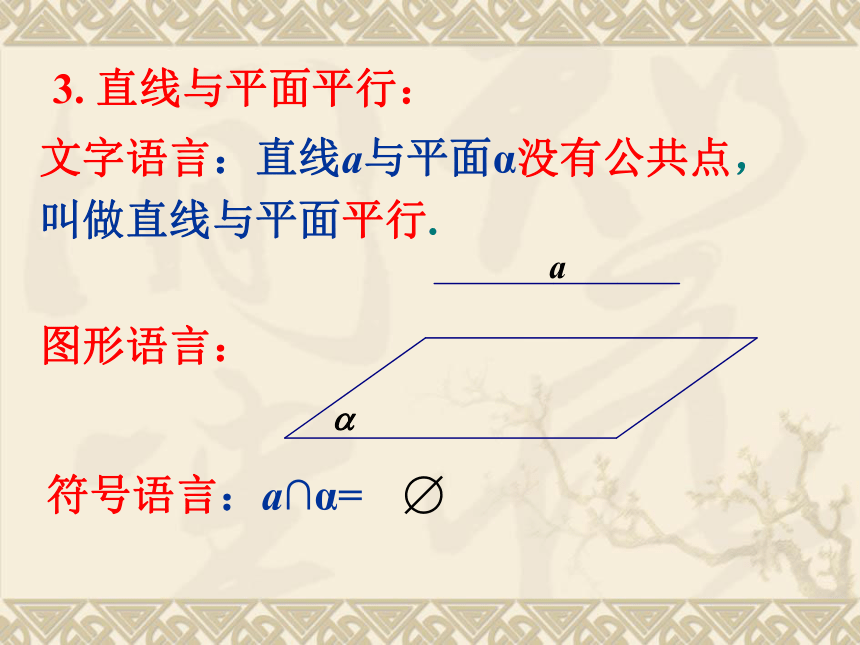
课件22张PPT。1.2.2空间中的平行关系(2)二. 直线与平面平行 1. 直线在平面内:文字语言:如果一条直线和一个平面有两个公共点,那么这条直线就在这个平面内。图形语言: 符号语言:A∈α,B∈α,2. 直线与平面相交:文字语言:直线a和平面α只有一个公共点A,叫做直线与平面相交,这个公共点叫做直线与平面的交点.图形语言: 符号语言:a∩α=A.3. 直线与平面平行:文字语言:直线a与平面α没有公共点,叫做直线与平面平行. 图形语言:符号语言:a∩α=3. 直线与平面平行的判定定理:(1)文字语言:如果不在一个平面内的一条直线和平面内的一条直线平行,那么这条直线和这个平面平行.(2)图形语言:(3)符号语言:
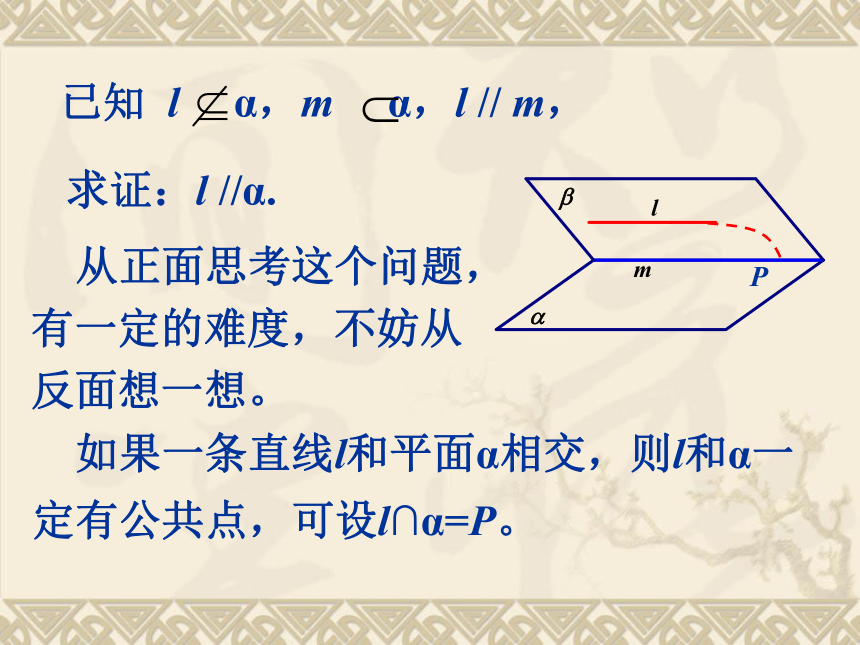
a α,b α, a // b, a //α.已知l α,m α,l // m,求证:l //α. 从正面思考这个问题,有一定的难度,不妨从反面想一想。 如果一条直线l和平面α相交,则l和α一定有公共点,可设l∩α=P。 再设l与m确定的平面为β,则依据平面基本性质3,点P一定在平面α与平面β的交线m上。于是l和m相交,这和l // m矛盾。所以可以断定l与α不可能有公共点。即l // α. 证明直线与平面平行,三个条件必须具备,才能得到线面平行的结论.运用定理的关键是找平行线;
找平行线又经常会用到三角形中位线定理. 三个条件中注意:“面外、面内、平行”4. 直线和平面平行的性质定理 (1)文字语言:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行. (2)图形语言: (3) 符号语言:a//b已知:l //α,l β,α∩β=m, 求证:l //m.证明:因为l //α,所以l与α没有公共点,又因为m在α内,所以l与m也没有公共点.因为l和m都在平面β内,且没有公共点,所以l //m.这条定理,由“线面平行”去判断“线线平行”例1. 已知空间四边形ABCD中,E,F分别是AB,AD的中点,求证:EF//平面BCD.证明:连接BD,在△ABD中,
因为E,F分别是AB,AD的中点,
所以EF // BD,又因为BD 平面BCD, EF 平面BCD,所以EF//平面BCD.例2. 求证:如果过一个平面内一点的直线平行于与该平面平行的一条直线,则这条直线在这个平面内。
已知:l //α,点P∈α,P∈m,m // l,求证:m α.证明:设l与P确定的平面为β,且α∩β=m’,则l //m’,又知l //m,m∩m’=P, 由平行公理可知,m与m’重合.所以m α. 例3.如图,正方体 中,E为 的中点,试判断 与平面AEC的位置关系,并说明理由.证明:连接BD交AC于点O,连接OE, 练习: 1.以下命题(其中a,b表示直线,?表示平面)
①若a∥b,b??,则a∥?
②若a∥?,b∥?,则a∥b
③若a∥b,b∥?,则a∥?
④若a∥?,b??,则a∥b
其中正确命题的个数是( )
(A)0个 (B)1个
(C)2个 (D)3个(4)过平面外一点和这个平面平行的直线只有一条.( )2.判断下列命题是否正确,若正确,请简述理由,若不正确,请给出反例.(1)如果a、b是两条直线,且a∥b,那么a 平行于经过b的任何平面;( )(2)如果直线a、b和平面α 满足a∥α,
b∥α,那么a∥b ;( )(3)如果直线a、b和平面α 满足a∥b, a∥α, b α, 那么 b∥α;( )3.在长方体
ABCD-A1B1C1D1中1.与直线AB平行的平面是______.2. 和直线AA1平行的平面是_____.3.与直线AD平行的平面是______.问题的关键是证明MN//AC,在⊿PAC中,证明PM:MA=PN:NC.4.证法1利用相似三角形对应边成比例
及平行线分线段成比例的性质∽∽证明2:
a α,b α, a // b, a //α.已知l α,m α,l // m,求证:l //α. 从正面思考这个问题,有一定的难度,不妨从反面想一想。 如果一条直线l和平面α相交,则l和α一定有公共点,可设l∩α=P。 再设l与m确定的平面为β,则依据平面基本性质3,点P一定在平面α与平面β的交线m上。于是l和m相交,这和l // m矛盾。所以可以断定l与α不可能有公共点。即l // α. 证明直线与平面平行,三个条件必须具备,才能得到线面平行的结论.运用定理的关键是找平行线;
找平行线又经常会用到三角形中位线定理. 三个条件中注意:“面外、面内、平行”4. 直线和平面平行的性质定理 (1)文字语言:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行. (2)图形语言: (3) 符号语言:a//b已知:l //α,l β,α∩β=m, 求证:l //m.证明:因为l //α,所以l与α没有公共点,又因为m在α内,所以l与m也没有公共点.因为l和m都在平面β内,且没有公共点,所以l //m.这条定理,由“线面平行”去判断“线线平行”例1. 已知空间四边形ABCD中,E,F分别是AB,AD的中点,求证:EF//平面BCD.证明:连接BD,在△ABD中,
因为E,F分别是AB,AD的中点,
所以EF // BD,又因为BD 平面BCD, EF 平面BCD,所以EF//平面BCD.例2. 求证:如果过一个平面内一点的直线平行于与该平面平行的一条直线,则这条直线在这个平面内。
已知:l //α,点P∈α,P∈m,m // l,求证:m α.证明:设l与P确定的平面为β,且α∩β=m’,则l //m’,又知l //m,m∩m’=P, 由平行公理可知,m与m’重合.所以m α. 例3.如图,正方体 中,E为 的中点,试判断 与平面AEC的位置关系,并说明理由.证明:连接BD交AC于点O,连接OE, 练习: 1.以下命题(其中a,b表示直线,?表示平面)
①若a∥b,b??,则a∥?
②若a∥?,b∥?,则a∥b
③若a∥b,b∥?,则a∥?
④若a∥?,b??,则a∥b
其中正确命题的个数是( )
(A)0个 (B)1个
(C)2个 (D)3个(4)过平面外一点和这个平面平行的直线只有一条.( )2.判断下列命题是否正确,若正确,请简述理由,若不正确,请给出反例.(1)如果a、b是两条直线,且a∥b,那么a 平行于经过b的任何平面;( )(2)如果直线a、b和平面α 满足a∥α,
b∥α,那么a∥b ;( )(3)如果直线a、b和平面α 满足a∥b, a∥α, b α, 那么 b∥α;( )3.在长方体
ABCD-A1B1C1D1中1.与直线AB平行的平面是______.2. 和直线AA1平行的平面是_____.3.与直线AD平行的平面是______.问题的关键是证明MN//AC,在⊿PAC中,证明PM:MA=PN:NC.4.证法1利用相似三角形对应边成比例
及平行线分线段成比例的性质∽∽证明2:
