1.1.2棱柱、棱锥和棱台的结构特征1
文档属性
| 名称 | 1.1.2棱柱、棱锥和棱台的结构特征1 |  | |
| 格式 | rar | ||
| 文件大小 | 142.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-11-04 13:31:00 | ||
图片预览




文档简介
课件29张PPT。1.1.2
棱柱、棱锥和棱台
的结构特征(1)一、知识回顾1.什么是几何体
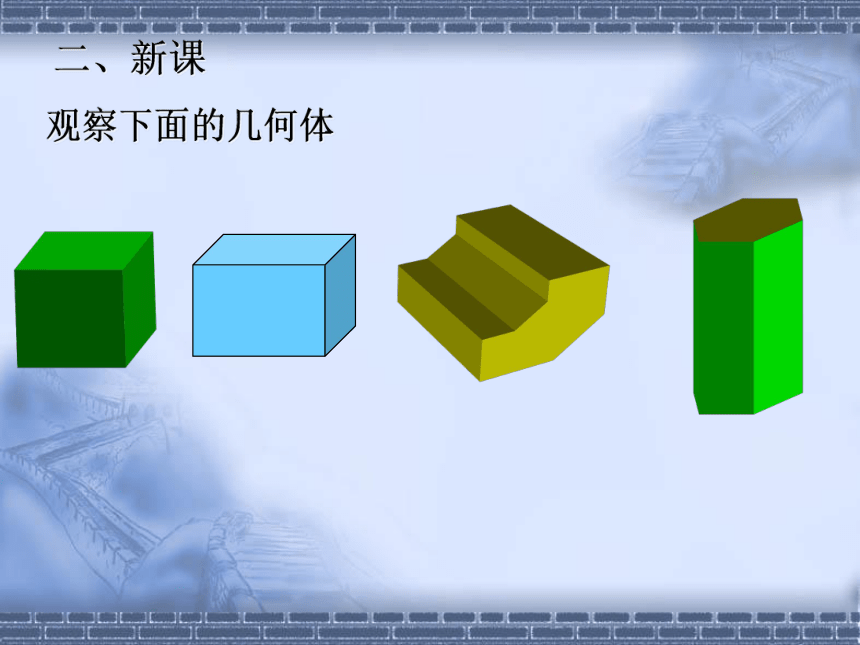
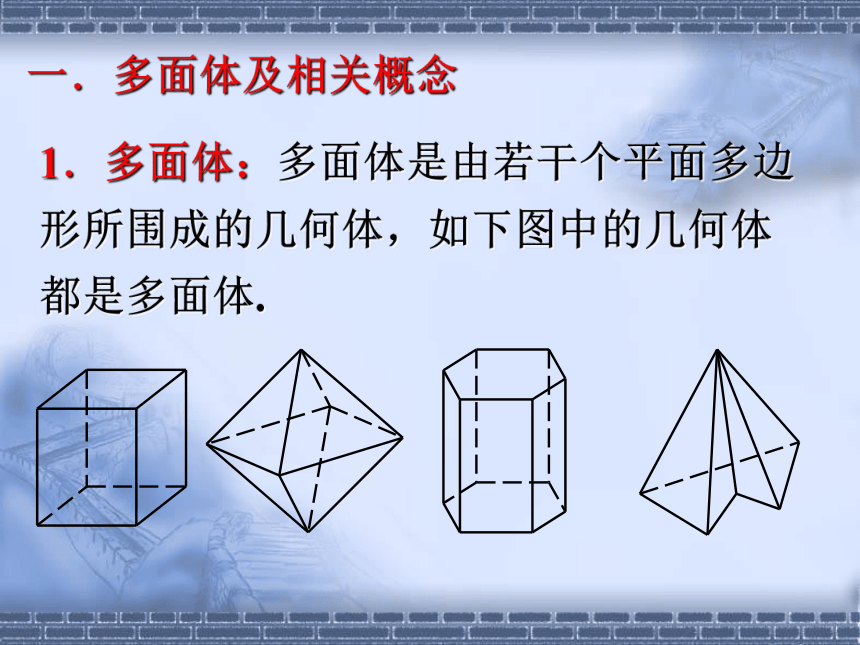
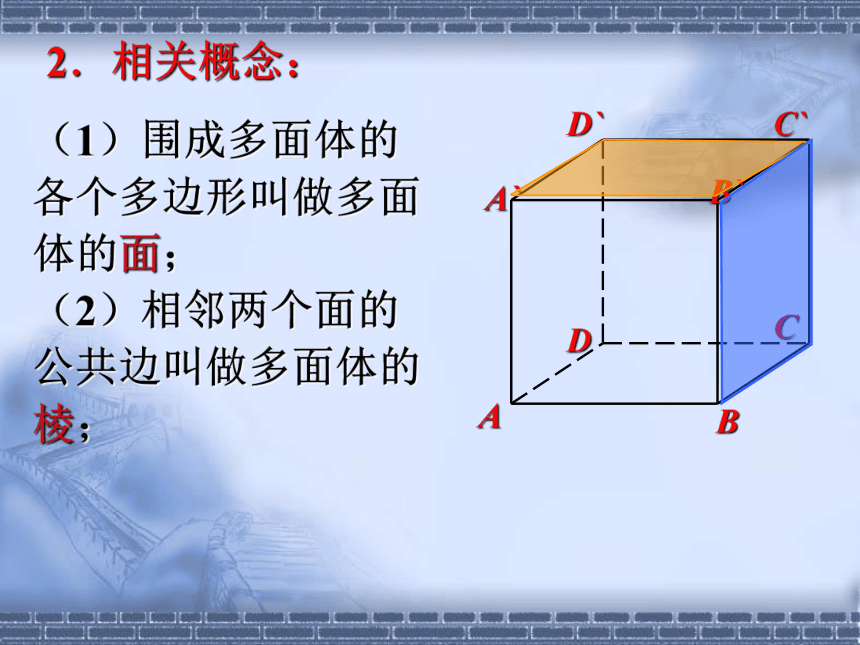
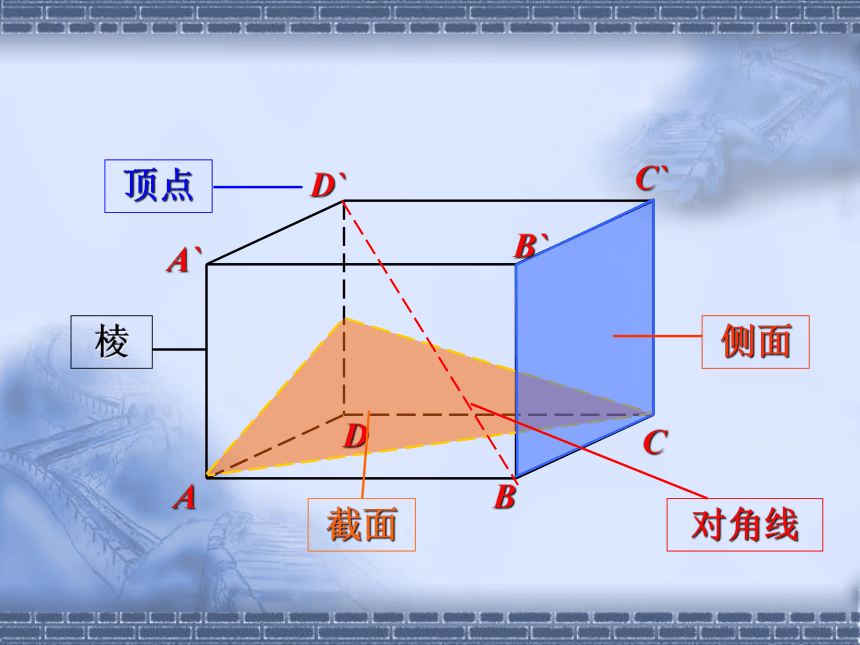
2.长方体的面、棱、顶点二、新课观察下面的几何体一.多面体及相关概念1.多面体:多面体是由若干个平面多边形所围成的几何体,如下图中的几何体都是多面体.(1)围成多面体的各个多边形叫做多面体的面;
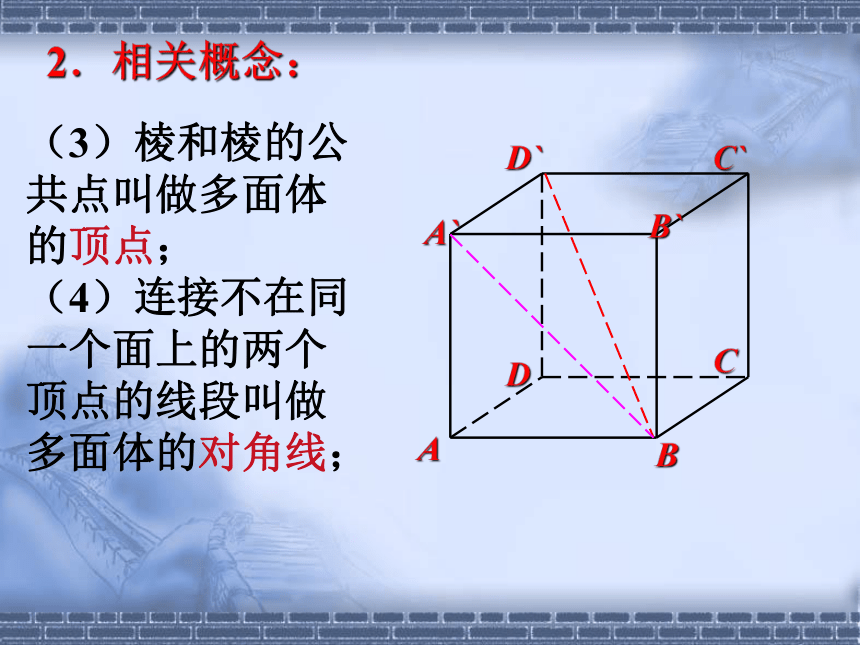
(2)相邻两个面的公共边叫做多面体的棱;2.相关概念:ABCDA`B`C`D`2.相关概念:(3)棱和棱的公共点叫做多面体的顶点;
(4)连接不在同一个面上的两个顶点的线段叫做多面体的对角线; ABCDA`B`C`D`(5)凸、凹多面体:把一个多面体的任意一个面延展为平面,如果其余各面都在这个平面的同一侧,则这样的多面体就叫做凸多面体,其他的多面体叫做凹多面体;
(6)截面:一个几何体和一个平面相交所得到的平面图形(包括它的内部),叫做这个几何体的截面;2.相关概念:ABCDA`B`C`D`3.多面体的分类:
(1)按照多面体是否在任一面的同一侧分为凸多面体和凹多面体;
(2)按照围成多面体的面的个数分为四面体、五面体、六面体等。观察下列多面体,根据小学、初中所学知识,判定它们是棱柱吗二. 棱柱及相关概念 1.定义: (1)棱柱的两个互相平行的面叫做棱柱的底面,简称底;
(2)其余各面叫做棱柱的侧面;
(3)相邻侧面的公共边叫做棱柱的侧棱;
(4)侧面与底面的公共顶点叫做棱柱的顶点;2.相关概念:(5)棱柱中不在同一面上的两个顶点的连线叫做棱柱的对角线 ;
(6)如果棱柱的一个底面水平放置,则铅垂线与两底面的交点之间的线段或距离,叫做棱柱的高。ABCDA`B`C`D`底
面侧
面侧
棱顶点对
角
线高如何理解棱柱?① 从运动的观点来看,棱柱可以看成是一个多边形(包括图形围成的平面部分)上各点都沿着同一个方向移动相同的距离所经过的空间部分。
如果多边形水平放置,则移动后的多边形也水平放置。② 棱柱的主要结构特征:
1)两个底面互相平行;
2)其余每相邻两个面的交线互相平行,
各侧面是平行四边形。如何理解棱柱?③ 但是注意“ 有两个面互相平行,其余各面都是平行四边 形”的几何体未必是棱柱。
如图所示的几何体虽有两个平面互相平行,其余各面都是平行四边形,但不满足“每相邻两个面的公共边互相平行”,所以它不是棱柱。如何理解棱柱?(1)按底面多边形的边数分为三棱柱、四棱柱、五棱柱等(见图)3.棱柱的分类:(2)按侧棱与底面的关系分类:
侧棱与底面不垂直的棱柱叫做斜棱柱;
侧棱与底面垂直的棱柱叫做直棱柱;
底面是正多边形的直棱柱叫做正棱柱。3.棱柱的分类:4.棱柱的表示:
(1)用表示各顶点的字母表示棱柱:如棱柱ABCD-A1B1C1D1;
(2)用一条对角线端点的两个字母来表示,如棱柱AC1.(1)底面是平行四边形的棱柱叫做平行六面体;
(2)侧棱与底面垂直的平行六面体叫做直平行六面体;5.特殊的四棱柱:5.特殊的四棱柱:(3)底面是矩形的直平行六面体叫做长方体;
(4)棱长都相等的长方体叫做正方体.四棱柱平行六面体长方体直平行六面体正四棱柱正方体底面是
平行四边形侧棱与底面
垂直底面是
矩形底面为
正方形侧棱与底面
边长相等几种四棱柱(六面体)的关系:例1.设有四个命题:
①底面是矩形的平行六面体是长方体;②棱长相等的直四棱柱是正方体;③有两条侧棱都垂直于底面一边的平行六面体是直平行六面体;④对角线相等的平行六面体是直平行六面体。以上四个命题中,真命题的个数是( )
(A)1 (B)2 (C)3 (D)4A例2.已知集合 A={正方体},B={长方体},C={正四棱柱},D={平行六面体},E={四棱柱},F={直平行六面体},则( )(A)
(B)
(C)
(D)它们之间不都存在包含关系 练习题:1.下面没有体对角线的一种几何体是( )
(A)三棱柱 (B)四棱柱
(C)五棱柱 (D)六棱柱2.用一个平面去截正方体,截面多边形的边数不可能是( )
(A)4 (B)5
(C)6 (D)73.一个棱柱有两个侧面是矩形,能保证它是直棱柱的是( )
(A)三棱柱 (B)四棱柱
(C)五棱柱 (D)六棱柱4.六棱柱有 条对角线.5.一个无盖的正方体盒子展开后的平面图形如图所示,A,B,C是展开图上的三点,同在正方体盒子中,∠ABC的大小是 。6.若两个长方体的长、宽、高分别为5cm、4cm、3cm,把它们两个相等的面重合在一起组成一个大长方体,则大长方体的对角线最长为 .
棱柱、棱锥和棱台
的结构特征(1)一、知识回顾1.什么是几何体
2.长方体的面、棱、顶点二、新课观察下面的几何体一.多面体及相关概念1.多面体:多面体是由若干个平面多边形所围成的几何体,如下图中的几何体都是多面体.(1)围成多面体的各个多边形叫做多面体的面;
(2)相邻两个面的公共边叫做多面体的棱;2.相关概念:ABCDA`B`C`D`2.相关概念:(3)棱和棱的公共点叫做多面体的顶点;
(4)连接不在同一个面上的两个顶点的线段叫做多面体的对角线; ABCDA`B`C`D`(5)凸、凹多面体:把一个多面体的任意一个面延展为平面,如果其余各面都在这个平面的同一侧,则这样的多面体就叫做凸多面体,其他的多面体叫做凹多面体;
(6)截面:一个几何体和一个平面相交所得到的平面图形(包括它的内部),叫做这个几何体的截面;2.相关概念:ABCDA`B`C`D`3.多面体的分类:
(1)按照多面体是否在任一面的同一侧分为凸多面体和凹多面体;
(2)按照围成多面体的面的个数分为四面体、五面体、六面体等。观察下列多面体,根据小学、初中所学知识,判定它们是棱柱吗二. 棱柱及相关概念 1.定义: (1)棱柱的两个互相平行的面叫做棱柱的底面,简称底;
(2)其余各面叫做棱柱的侧面;
(3)相邻侧面的公共边叫做棱柱的侧棱;
(4)侧面与底面的公共顶点叫做棱柱的顶点;2.相关概念:(5)棱柱中不在同一面上的两个顶点的连线叫做棱柱的对角线 ;
(6)如果棱柱的一个底面水平放置,则铅垂线与两底面的交点之间的线段或距离,叫做棱柱的高。ABCDA`B`C`D`底
面侧
面侧
棱顶点对
角
线高如何理解棱柱?① 从运动的观点来看,棱柱可以看成是一个多边形(包括图形围成的平面部分)上各点都沿着同一个方向移动相同的距离所经过的空间部分。
如果多边形水平放置,则移动后的多边形也水平放置。② 棱柱的主要结构特征:
1)两个底面互相平行;
2)其余每相邻两个面的交线互相平行,
各侧面是平行四边形。如何理解棱柱?③ 但是注意“ 有两个面互相平行,其余各面都是平行四边 形”的几何体未必是棱柱。
如图所示的几何体虽有两个平面互相平行,其余各面都是平行四边形,但不满足“每相邻两个面的公共边互相平行”,所以它不是棱柱。如何理解棱柱?(1)按底面多边形的边数分为三棱柱、四棱柱、五棱柱等(见图)3.棱柱的分类:(2)按侧棱与底面的关系分类:
侧棱与底面不垂直的棱柱叫做斜棱柱;
侧棱与底面垂直的棱柱叫做直棱柱;
底面是正多边形的直棱柱叫做正棱柱。3.棱柱的分类:4.棱柱的表示:
(1)用表示各顶点的字母表示棱柱:如棱柱ABCD-A1B1C1D1;
(2)用一条对角线端点的两个字母来表示,如棱柱AC1.(1)底面是平行四边形的棱柱叫做平行六面体;
(2)侧棱与底面垂直的平行六面体叫做直平行六面体;5.特殊的四棱柱:5.特殊的四棱柱:(3)底面是矩形的直平行六面体叫做长方体;
(4)棱长都相等的长方体叫做正方体.四棱柱平行六面体长方体直平行六面体正四棱柱正方体底面是
平行四边形侧棱与底面
垂直底面是
矩形底面为
正方形侧棱与底面
边长相等几种四棱柱(六面体)的关系:例1.设有四个命题:
①底面是矩形的平行六面体是长方体;②棱长相等的直四棱柱是正方体;③有两条侧棱都垂直于底面一边的平行六面体是直平行六面体;④对角线相等的平行六面体是直平行六面体。以上四个命题中,真命题的个数是( )
(A)1 (B)2 (C)3 (D)4A例2.已知集合 A={正方体},B={长方体},C={正四棱柱},D={平行六面体},E={四棱柱},F={直平行六面体},则( )(A)
(B)
(C)
(D)它们之间不都存在包含关系 练习题:1.下面没有体对角线的一种几何体是( )
(A)三棱柱 (B)四棱柱
(C)五棱柱 (D)六棱柱2.用一个平面去截正方体,截面多边形的边数不可能是( )
(A)4 (B)5
(C)6 (D)73.一个棱柱有两个侧面是矩形,能保证它是直棱柱的是( )
(A)三棱柱 (B)四棱柱
(C)五棱柱 (D)六棱柱4.六棱柱有 条对角线.5.一个无盖的正方体盒子展开后的平面图形如图所示,A,B,C是展开图上的三点,同在正方体盒子中,∠ABC的大小是 。6.若两个长方体的长、宽、高分别为5cm、4cm、3cm,把它们两个相等的面重合在一起组成一个大长方体,则大长方体的对角线最长为 .
