13.3实数
图片预览






文档简介
课件29张PPT。13.3 实数人教版《数学》八年级 上册学习目标1. 了解无理数和实数的概念, 能对实数按要求分类;
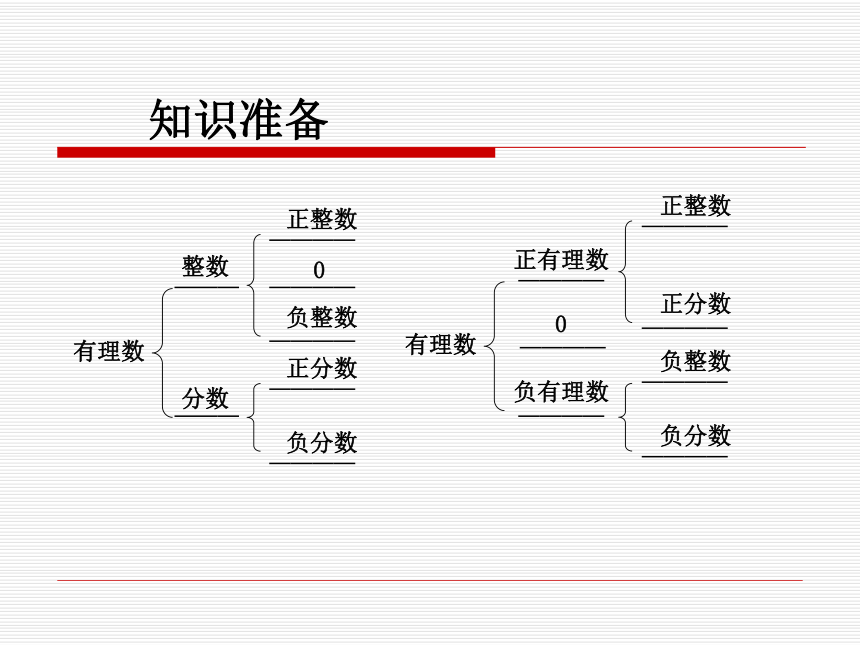
2. 知道实数与数轴上的点具有 一一对应关系。 ————知识准备有理数有理数——————————————————————————————————————————————————(1)观察下列有理数写成小数的形式,你有什么发现?任何有理数都能写成有限小数和无限循环小数吗?
(2)请用计算器把 和 写成小数的形式,你有什么发现?像这样的数我们把它叫什么数?你还能说出一些这样的数吗?
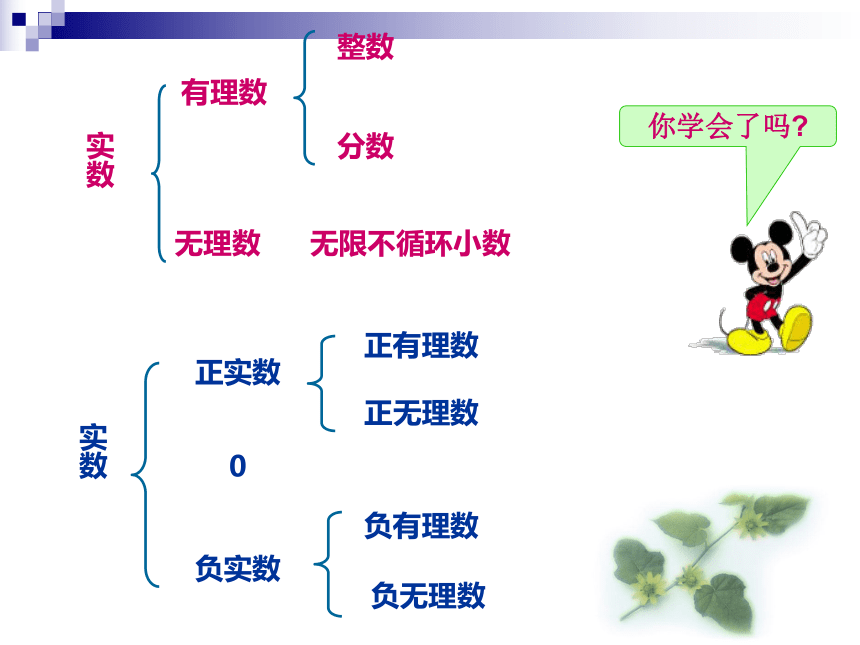
(3)我们把哪些数统称为实数?你能把实数进行分类吗?
事实上,任何一个有理数都可以写成有限小数或无限循环小数.反过来,任何有限小数或无限循环小数也都是有理数.∵ 12=1, 22=4∴ 1 < < 2∵ 1.42=1.96, 1.52=2.25∴ 1.4 < < 1.5∵ 1.412=1.9881, 1.422=2.0164∴ 1.41 < < 1.42∵ 1.4142=1.9881, 1.4152=2.002225∴ 1.414 < < 1.415 是一个有理数吗?讨 论 无限不循环的小数 ---------- 叫做无理数.你能举出一些无理数吗?0.1010010001…〔两个1之间依次多1个0〕—168.3232232223…〔两个3之间依次多1个2〕有理数和无理数统称实数.实数实数有理数无理数整数分数无限不循环小数正实数 0负实数正有理数正无理数负有理数负无理数你学会了吗?试一试
把下列各数分别填入相应的集合内:(相邻两个3之间的7的个数逐次加1) 有理数集合 无理数集合整数有
有理数有
无理数有
实数有二、填空在实数
中,
每个有理数都可以用数轴上的点表示,那么无理数是否也可以用数轴上的点表示出来吗?﹒A能在数轴上找到表示π的点吗?
试一试你能把 在数轴上表示出来吗?请与同桌一起试一试。问题:边长为1的正方形,对角线长为多少?也就是说:每一个无理数都可以用数轴上的一个点来表示.数轴上的点有些表示有理数,有些表示无理数.想一想有理数能不能将数轴排满?一、判断下列说法是否正确:1.实数不是有理数就是无理数。 ( )
2.无限小数都是无理数。 ( )
3.无理数都是无限小数。 ( )
4.带根号的数都是无理数。 ( )
6.所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数。( )
5.无理数一定都带根号。 ( )8.两个无理数之积不一定是无理数。( )9.有理数与无理数之和一定是无理数 ( )7.两个无理数之和一定是无理数。( )实数与数轴上的点是一一对应的.同样的,平面直角坐标系中的点与有序实数对是一一对应的.探究新知-1.5π3试用“夹值法”或计算器估算下列各数的值,按从小到大的顺序排列,并找到数轴上与之对应的点数轴上任意两点,左边的点表示的实数总比右边的小;
反之,右边的点表示的实数总比左边的大。学以致用1.如图,数轴上点P表示的数可能是( )
A B C D-3.22.如下图,数轴上表示 的点是______3.假设上图中的A、B、C三个点都表示无理数,其中最小的无理数可能是_____BBA 在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。填空2、 的相反数是 ,绝对值是 .3、绝对值等于 的数是 , 的平 方 是 .4、比较大小:-7 1、正实数的绝对值是 ,0的绝对值是 ,负实数的绝对值是 .它本身0它的相反数5、一个数的绝对值是 ,则这个数是 .(1)分别写出- , 的相反数;(2)指出(3)求(4)已知一个数的绝对值是求这个数.练习:
2.求下列各数的相反数和绝值:
例2 计算下列各式的值:
练习: 4. 计算:
例3.计算:(结果保留小数点后两位)
课堂小结这节课你有什么新发现?知道了哪些新知识? 谢谢!祝同学们学习进步!
2. 知道实数与数轴上的点具有 一一对应关系。 ————知识准备有理数有理数——————————————————————————————————————————————————(1)观察下列有理数写成小数的形式,你有什么发现?任何有理数都能写成有限小数和无限循环小数吗?
(2)请用计算器把 和 写成小数的形式,你有什么发现?像这样的数我们把它叫什么数?你还能说出一些这样的数吗?
(3)我们把哪些数统称为实数?你能把实数进行分类吗?
事实上,任何一个有理数都可以写成有限小数或无限循环小数.反过来,任何有限小数或无限循环小数也都是有理数.∵ 12=1, 22=4∴ 1 < < 2∵ 1.42=1.96, 1.52=2.25∴ 1.4 < < 1.5∵ 1.412=1.9881, 1.422=2.0164∴ 1.41 < < 1.42∵ 1.4142=1.9881, 1.4152=2.002225∴ 1.414 < < 1.415 是一个有理数吗?讨 论 无限不循环的小数 ---------- 叫做无理数.你能举出一些无理数吗?0.1010010001…〔两个1之间依次多1个0〕—168.3232232223…〔两个3之间依次多1个2〕有理数和无理数统称实数.实数实数有理数无理数整数分数无限不循环小数正实数 0负实数正有理数正无理数负有理数负无理数你学会了吗?试一试
把下列各数分别填入相应的集合内:(相邻两个3之间的7的个数逐次加1) 有理数集合 无理数集合整数有
有理数有
无理数有
实数有二、填空在实数
中,
每个有理数都可以用数轴上的点表示,那么无理数是否也可以用数轴上的点表示出来吗?﹒A能在数轴上找到表示π的点吗?
试一试你能把 在数轴上表示出来吗?请与同桌一起试一试。问题:边长为1的正方形,对角线长为多少?也就是说:每一个无理数都可以用数轴上的一个点来表示.数轴上的点有些表示有理数,有些表示无理数.想一想有理数能不能将数轴排满?一、判断下列说法是否正确:1.实数不是有理数就是无理数。 ( )
2.无限小数都是无理数。 ( )
3.无理数都是无限小数。 ( )
4.带根号的数都是无理数。 ( )
6.所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数。( )
5.无理数一定都带根号。 ( )8.两个无理数之积不一定是无理数。( )9.有理数与无理数之和一定是无理数 ( )7.两个无理数之和一定是无理数。( )实数与数轴上的点是一一对应的.同样的,平面直角坐标系中的点与有序实数对是一一对应的.探究新知-1.5π3试用“夹值法”或计算器估算下列各数的值,按从小到大的顺序排列,并找到数轴上与之对应的点数轴上任意两点,左边的点表示的实数总比右边的小;
反之,右边的点表示的实数总比左边的大。学以致用1.如图,数轴上点P表示的数可能是( )
A B C D-3.22.如下图,数轴上表示 的点是______3.假设上图中的A、B、C三个点都表示无理数,其中最小的无理数可能是_____BBA 在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。填空2、 的相反数是 ,绝对值是 .3、绝对值等于 的数是 , 的平 方 是 .4、比较大小:-7 1、正实数的绝对值是 ,0的绝对值是 ,负实数的绝对值是 .它本身0它的相反数5、一个数的绝对值是 ,则这个数是 .(1)分别写出- , 的相反数;(2)指出(3)求(4)已知一个数的绝对值是求这个数.练习:
2.求下列各数的相反数和绝值:
例2 计算下列各式的值:
练习: 4. 计算:
例3.计算:(结果保留小数点后两位)
课堂小结这节课你有什么新发现?知道了哪些新知识? 谢谢!祝同学们学习进步!
