（苏科版九年级上）数学：4.1圆课件

课件20张PPT。圆要点、考点聚焦
课前热身
典型例题解析
课时训练 要点、考点聚焦1.本课时重点是垂径定理及其推论，圆心角、
圆周角、弦心距、弧之间的关系.
2.圆的定义
(1)是通过旋转.
(2)是到定点的距离等于定长的点的集合.3.点和圆的位置关系(圆心到点的距离为d)
(1)点在圆上?d=r.
(2)点在圆内?d＜r.
(3)点在圆外?d＞r.
4.与圆有关的概念
(1)弦：连结圆上任意两点的线段.
(2)直径：经过圆心的弦.
(3)弧：圆上任意两点间的部分.
(4)优弧：劣弧、半圆.
(5)等弧：在同圆或等圆中，能够完全重合的孤.
(6)圆心角：顶点在圆心，角的两边与圆相交.
(7)圆周角：顶点在圆上，角的两边与圆相交.
(8)三角形外心及性质.要点、考点聚焦垂径定理：垂直于弦的直径平分弦，并且平分弦
所对的两条弧.推论1：平分弦(不是直径)的直径垂直于弦，并且
平分弦所对的两条弧.
推论2：弦的垂直平分线经过圆心，并且平分弦
所对的两条弧.
推论3：平分弦所对的一条弧的直径，垂直平分
弦，并平分弦所对的另一条弧.5.有关定理及推论
(1)定理：不在同一直线上的三个点确定一个圆.
(2)垂径定理及其推论. 要点、考点聚焦(4)圆周角定理：一条弧所对圆周角等于它所对的圆心角的一半. 推论1：同弧或等弧所对的圆周角相等；同圆或等圆
中，相等的圆周角所对的弧也相等.
推论2：半圆(或直径)所对的圆周角是直角；90°的圆
周角所对的弦是直径.
推论3：如果三角形一边上的中线等于这边的一半，
那么这个三角形是直角三角形.定理：在同圆或等圆中，相等的圆心角所对的弧
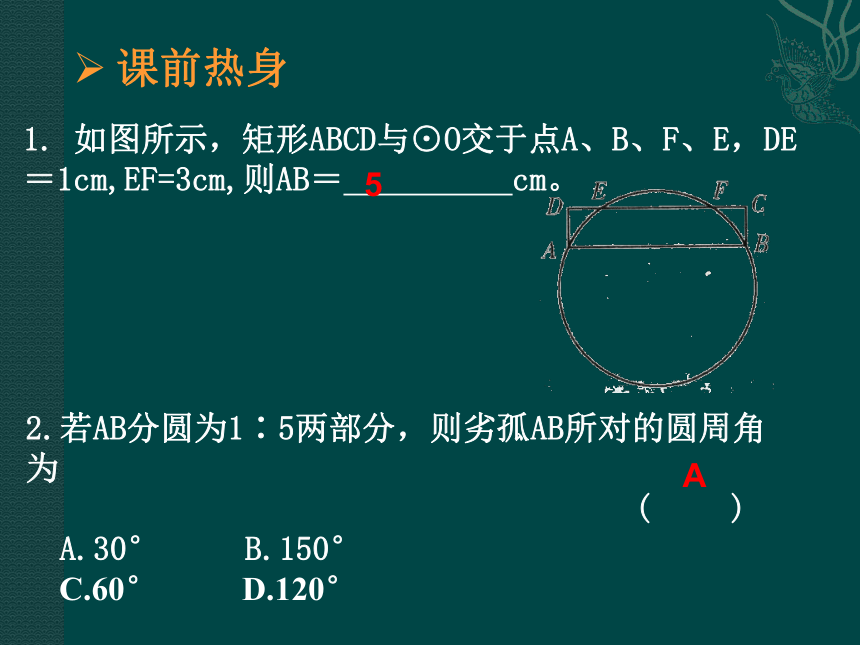
相等，所对的弦相等，所对弦的弦心距相等. (3)圆心角、弧、弦、弦心距. 要点、考点聚焦6.中考题型：这部分题目变化灵活，在历年各地中考试题中均占有较大比例，就考查的形式来看，不仅可以单独考查，而且往往与几何前几章知识以及方程、函数等知识相结合.(5)圆内接四边形性质定理：圆内接四边形的对角互补，并且任何一个外角都等于它的内对角. 要点、考点聚焦课前热身1. 如图所示，矩形ABCD与⊙O交于点A、B、F、E，DE＝1cm,EF=3cm,则AB＝ cm。 2.若AB分圆为1∶5两部分，则劣孤AB所对的圆周角为
( )
A.30° B.150°
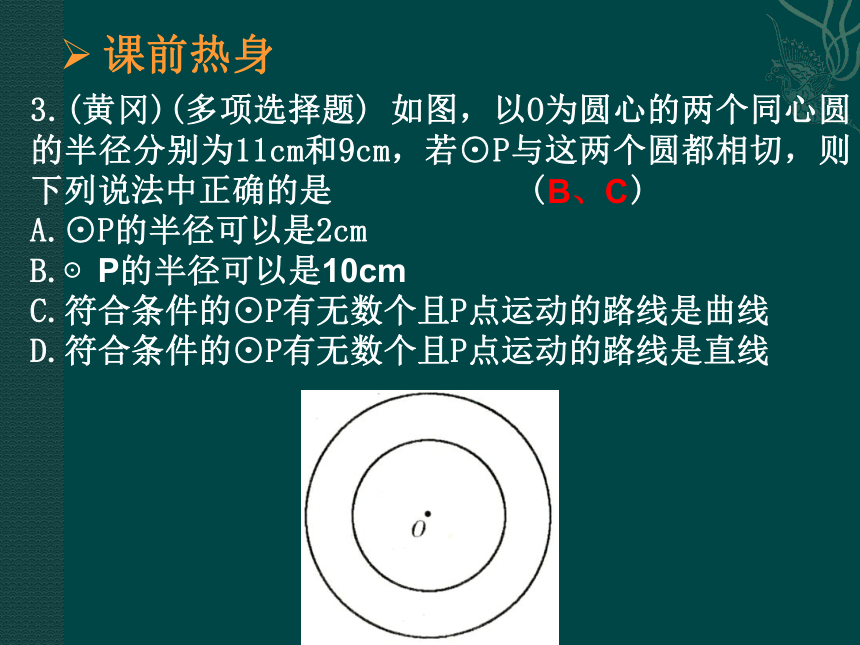
C.60° D.120° 5A3.(黄冈)(多项选择题) 如图，以O为圆心的两个同心圆的半径分别为11cm和9cm，若⊙P与这两个圆都相切，则下列说法中正确的是 ( )
A.⊙P的半径可以是2cm
B.⊙P的半径可以是10cm
C.符合条件的⊙P有无数个且P点运动的路线是曲线
D.符合条件的⊙P有无数个且P点运动的路线是直线 B、C课前热身5.下列说法中，正确的是 ( )
A.到圆心的距离大于半径的点在圆内
B.圆周角等于圆心角的一半
C.等弧所对的圆心角相等
D.三点确定一个圆C4.(昆明市)如图所示，是中国共产主义青年团团旗上的图案，点A、B、C、D、E五等分圆，则∠A+∠B+∠C+∠D+∠E的度数是 ( )
A.180° B.150°
C.135° D.120° A课前热身典型例题解析【例1】在直径为400mm的圆柱形油槽内，装入一部分油，油面宽320mm，求油的深度.【解析】本题是以垂径定理为考查点的几何应用题，没
有给出图形，直径长是已知的，油面宽可理解为截面圆
的弦长，也是已知的，但由于圆的对称性，弦的位置有
两种不同的情况，如图(1)和(2)图(1)中
OC=
=120(mm)
∴CD=80(mm)
图(2)中OC=120(mm)
∴CD=OC+OD=320(mm)【例2】(广州市)如图，A是半径为5的⊙O内的一点，且OA=3，过点A且长小于8的弦有 ( )
A.0条 B.1条
C.2条 D.4条 A【解析】这题是考察垂径定理的几何题，先求出垂直于OA的弦长BC=2 =8即过A点最短的弦长为8，故没有弦长
小于8的弦，∴选(A)典型例题解析【例3】如图，O是∠CAE平分线上的一点，以点O为圆心的圆和∠CAE的两边分别交于点B、C和D、E，连结BD、CE.

求证：
(1)BC=DE (2)AC=AE (3)DB∥CE. 典型例题解析【解析】
(1)要证弧相等，即要证弦相等或弦心距离相等，
又已知OA是∠CAE的平分线，联想到角平分线性质，
故过O分别作OG⊥AC于G，
OH⊥AE于H，
∴OG=OH
∴BC=DE
(2)由垂径定理知：BC=DE，G、H分别是BC、DE的中点.
再由△AOG≌△AOH?
AG=AH?AB=AD AC=AE.
(3)AC=AE?∠C=∠E，再根据圆的内接四边形的
性质定理知∠C=∠ADB?∠E=∠ADB?BD∥CE.
【例4】一只狸猫观察到一老鼠洞的全部三个出口，它们不在一条直线上，这只狸猫应蹲在何处，才能最省力地顾及到三个洞口?【解析】在农村、城镇上这是一个狸猫捉老鼠会遇到的一个问题，我们可以为这个小动物设计或计算出来.这个问题应考虑两种情况：设三个洞口分别为A、B、C三点，又设A、C相距最远
①当△ABC为钝角三角形或直角三角形时，AC的中点即为所求.
②当△ABC为锐角三角形时，△ABC的外心即为所求.
典型例题解析方法小结：1.常利用弦心距，弦的一半及半径构成直角三角形.
2.遇直径条件时，常构造直径所对的圆周角，得到90°
的角.课时训练1.如图，设⊙O的半径为r，弦AB的长为a，弦心距
OD=d且OC⊥AB于D，弓形高CD为h，下面的说法或等式：
①r=d+h
②4r2=4d2+a2
③已知：r、a、d、h中的任两个可求其他两个，
其中正确的结论的序号是( )
?A.① B.①②
C.①②③ D.②③C2.(上海)下列命题中，正确的是（多项选择题）
( )
A.一个点到圆心的距离大于这个圆的半径，这个点在
圆外
B.一条直线垂直于圆的半径，这条直线一定是圆的切线
C.两圆的圆心距等于它们的半径之和，这两个圆有三条
公切线
D.圆心到一条直线的距离小于这个圆的半径，这条直线
与圆有两个交点 A、C、D课时训练3.(山西)如图所示，已知RtΔABC中，∠C=90°,AC= ,BC=1,若以C为圆心，CB为半径的圆交AB于P，则AP＝ 。 课时训练课时训练30°5.半径为1的圆中有一条弦，如果它的长为 ，那么这条弦所对的圆周角为 ( )
A.60° B.120°
C.45° D.60°或120°D6.(江苏苏州市)如图，四边形ABCD内接于⊙O，若它的一个外角∠DCE=70°，则∠BOD=( )
A．35° B.70°
C．110° D.140° D课时训练