2.3数学活动 探索规律
文档属性
| 名称 | 2.3数学活动 探索规律 |

|
|
| 格式 | rar | ||
| 文件大小 | 551.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-11-03 00:00:00 | ||
图片预览


文档简介
课件17张PPT。探 索 规 律第二章 数学活动课“没有大胆的猜想,就做不出伟大的成果。”
——牛顿 “要成为一个好的数学家,你必须是一个好的猜想家。” ——波利亚
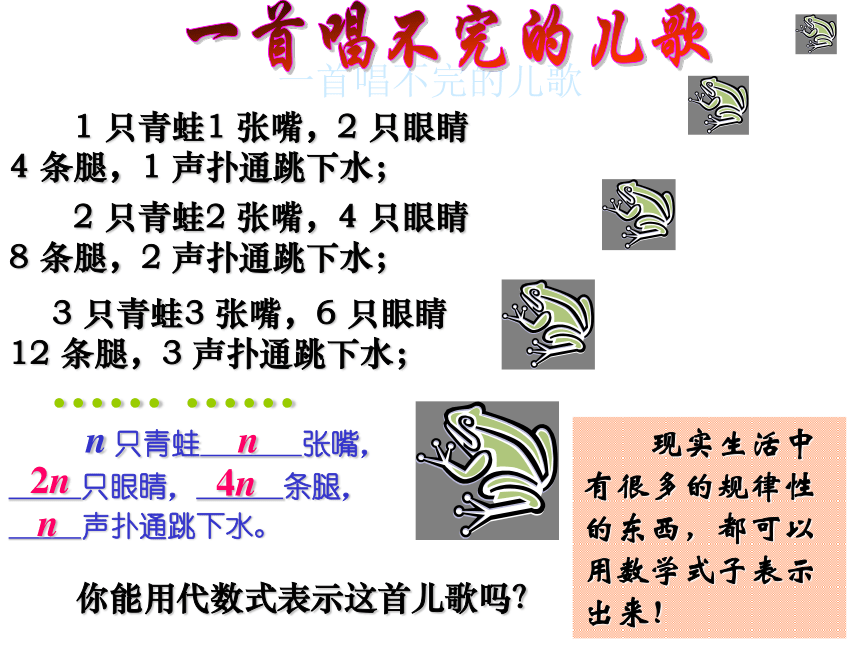
一首唱不完的儿歌一首唱不完的儿歌 现实生活中有很多的规律性的东西,都可以用数学式子表示出来!······ ······ 你能用代数式表示这首儿歌吗? n 只青蛙 张嘴,
只眼睛, 条腿,
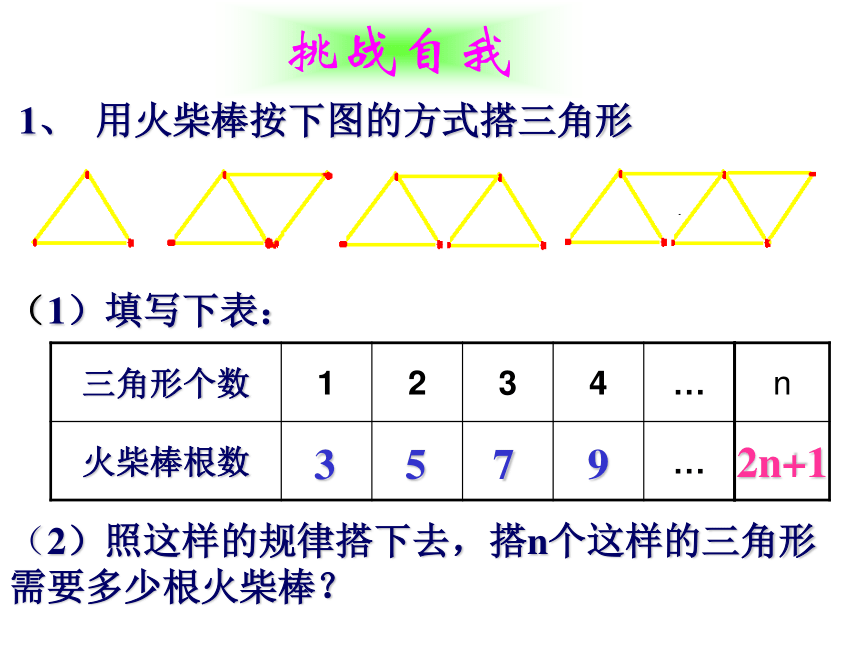
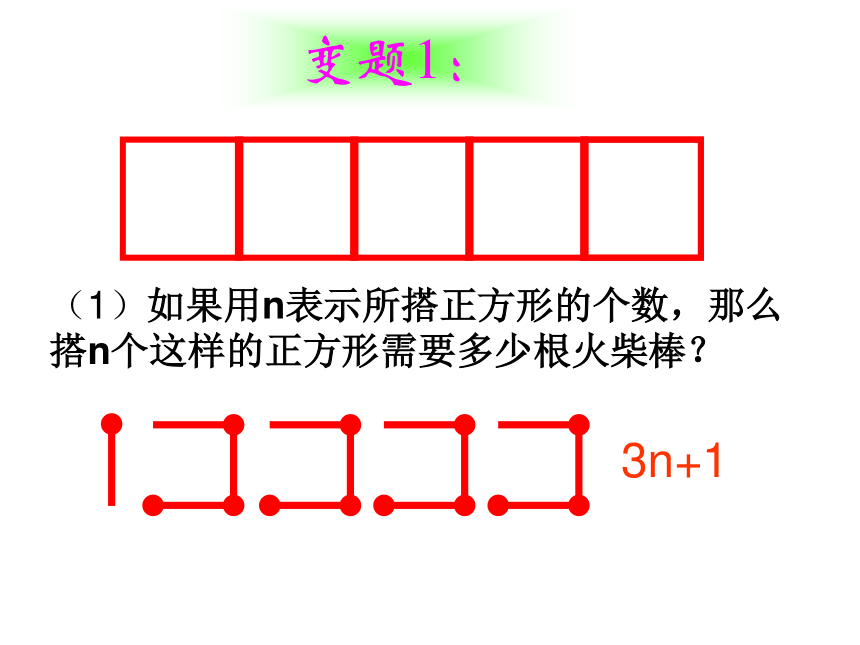
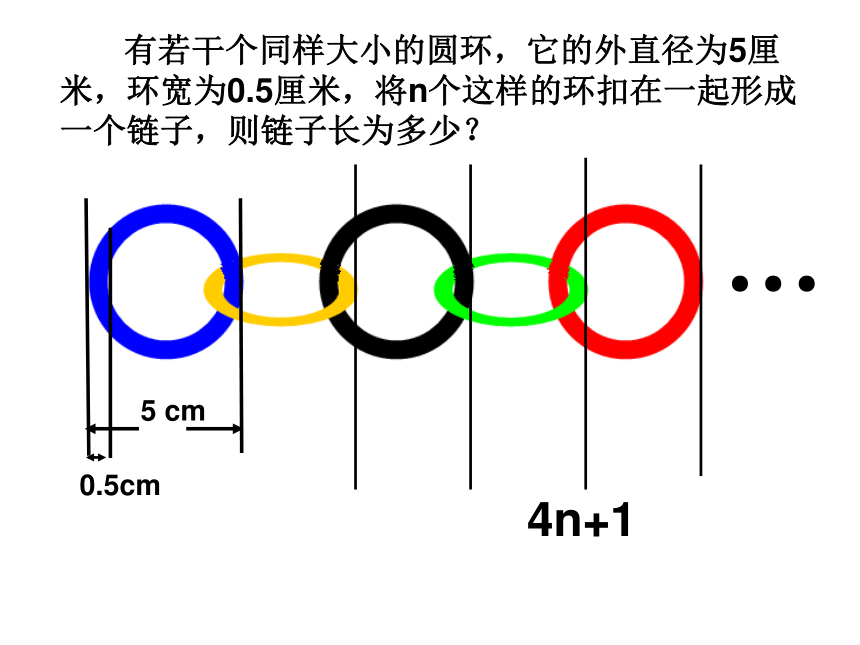
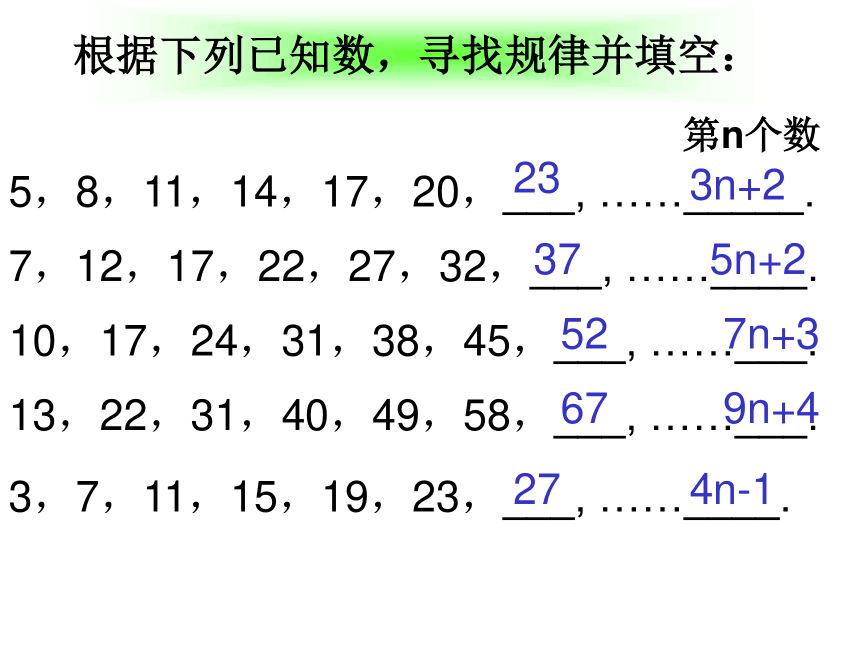
声扑通跳下水。n2n4nn1、 用火柴棒按下图的方式搭三角形 (2)照这样的规律搭下去,搭n个这样的三角形需要多少根火柴棒?(1)填写下表:挑战自我35792n+1(1)如果用n表示所搭正方形的个数,那么搭n个这样的正方形需要多少根火柴棒?3n+1变题1:扣一 扣---五环变题2: ● ● ●0.5cm5 cm 有若干个同样大小的圆环,它的外直径为5厘米,环宽为0.5厘米,将n个这样的环扣在一起形成一个链子,则链子长为多少?4n+1正方形2根据下列已知数,寻找规律并填空:7,12,17,22,27,32,___, ……____.第n个数10,17,24,31,38,45,___, ……___.13,22,31,40,49,58,___, ……___.5,8,11,14,17,20,___, ……_____.3,7,11,15,19,23,___, ……____.233n+2375n+2527n+39n+467274n-1练一练1、如图,用大小相等的小正方形拼成大正方形,拼第1个正方形4个小正方形,拼第2个正方形需要9个小正方形……拼一拼,想一想,按照这样的方法拼成的第n个正方形比第(n-1)个正方形多几个正方形?2n+1探索日历中的规律●右图是某月的日历。你发现这些数字有什么特点了吗?
数与数之间有什么关系?
横行相邻两数相差1,
竖列相邻两数相差7。(1)带阴影的方框中的9个数之和与该方框正中心的数有什么关系?9 倍(2)这个关系对其它这样的方框成立吗?成立 若设套色方框中正中间的数为a ,则这九个数之和是 。9 a日 历 中 的 数 字 规 律 (4)这个关系对任何一个月的日历都成立吗? 若设套色方框中正中间的数为 a ,则这九个数之和是 9a。成立因为这九个数可表示为:a-1a + 1a-7a + 7a-8a-6a + 6a + 8 将这九个数相加,正好等于9a 。日 历 中 的 数 字 规 律(3)你能证明你的结论吗? 若设套色方框中正中间的数为 a , 则这九个数可表示为右图。a-1则这九个数之和是 9a。a-7a + 7a-8a-6a + 6a + 8a + 1 各行三数之和都是正中间的数的 。3 倍日 历 中 的 数 字 规 律
1、在右图的日历中,任意圈出一竖列上相邻的三个数,设中间的一个数为a,则这三个数之和为
。
(用含a的代数式表示)
练一练3a2、设中间数为a,则十字形区域中的五个数的和为________。5a请你用一个等式表示a、b、c、d之间的关系: 。3、如图是2002年6月的日历。现用一个矩形在日历中任意框出4个数,
a+d=b+c如果设左上角的数为a,则这四个数的和为:_________.4a+16若左下角的数为a呢?观察、比较猜想、验证推理、分析探索规律的一般思路:用符号(或字母)表示实际问题的一般规律,并用运算来验证一般规律。小 结在探索规律中遇到挫折,你会怎么办?特殊一般简单复杂
——牛顿 “要成为一个好的数学家,你必须是一个好的猜想家。” ——波利亚
一首唱不完的儿歌一首唱不完的儿歌 现实生活中有很多的规律性的东西,都可以用数学式子表示出来!······ ······ 你能用代数式表示这首儿歌吗? n 只青蛙 张嘴,
只眼睛, 条腿,
声扑通跳下水。n2n4nn1、 用火柴棒按下图的方式搭三角形 (2)照这样的规律搭下去,搭n个这样的三角形需要多少根火柴棒?(1)填写下表:挑战自我35792n+1(1)如果用n表示所搭正方形的个数,那么搭n个这样的正方形需要多少根火柴棒?3n+1变题1:扣一 扣---五环变题2: ● ● ●0.5cm5 cm 有若干个同样大小的圆环,它的外直径为5厘米,环宽为0.5厘米,将n个这样的环扣在一起形成一个链子,则链子长为多少?4n+1正方形2根据下列已知数,寻找规律并填空:7,12,17,22,27,32,___, ……____.第n个数10,17,24,31,38,45,___, ……___.13,22,31,40,49,58,___, ……___.5,8,11,14,17,20,___, ……_____.3,7,11,15,19,23,___, ……____.233n+2375n+2527n+39n+467274n-1练一练1、如图,用大小相等的小正方形拼成大正方形,拼第1个正方形4个小正方形,拼第2个正方形需要9个小正方形……拼一拼,想一想,按照这样的方法拼成的第n个正方形比第(n-1)个正方形多几个正方形?2n+1探索日历中的规律●右图是某月的日历。你发现这些数字有什么特点了吗?
数与数之间有什么关系?
横行相邻两数相差1,
竖列相邻两数相差7。(1)带阴影的方框中的9个数之和与该方框正中心的数有什么关系?9 倍(2)这个关系对其它这样的方框成立吗?成立 若设套色方框中正中间的数为a ,则这九个数之和是 。9 a日 历 中 的 数 字 规 律 (4)这个关系对任何一个月的日历都成立吗? 若设套色方框中正中间的数为 a ,则这九个数之和是 9a。成立因为这九个数可表示为:a-1a + 1a-7a + 7a-8a-6a + 6a + 8 将这九个数相加,正好等于9a 。日 历 中 的 数 字 规 律(3)你能证明你的结论吗? 若设套色方框中正中间的数为 a , 则这九个数可表示为右图。a-1则这九个数之和是 9a。a-7a + 7a-8a-6a + 6a + 8a + 1 各行三数之和都是正中间的数的 。3 倍日 历 中 的 数 字 规 律
1、在右图的日历中,任意圈出一竖列上相邻的三个数,设中间的一个数为a,则这三个数之和为
。
(用含a的代数式表示)
练一练3a2、设中间数为a,则十字形区域中的五个数的和为________。5a请你用一个等式表示a、b、c、d之间的关系: 。3、如图是2002年6月的日历。现用一个矩形在日历中任意框出4个数,
a+d=b+c如果设左上角的数为a,则这四个数的和为:_________.4a+16若左下角的数为a呢?观察、比较猜想、验证推理、分析探索规律的一般思路:用符号(或字母)表示实际问题的一般规律,并用运算来验证一般规律。小 结在探索规律中遇到挫折,你会怎么办?特殊一般简单复杂
