3.6.1垂线
图片预览

文档简介
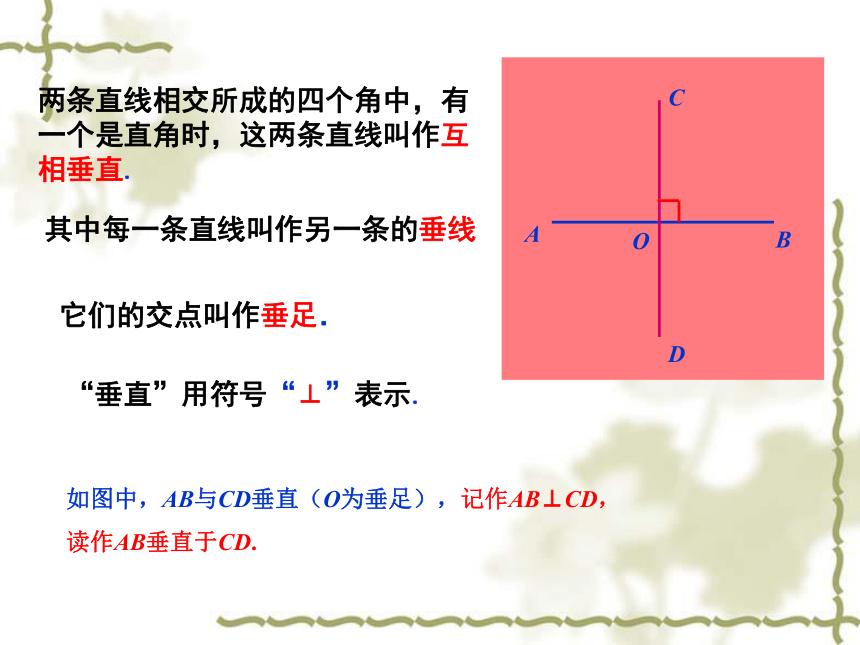
课件9张PPT。第3章 平面上直线的位置关系和度量关系3.6 垂线的性质与判定3.6.1 垂 线 画框的边线,十字路口两条笔直的街道,屋架的横梁与支撑等都相交成多少度的角?它们的交点叫作垂足.两条直线相交所成的四个角中,有一个是直角时,这两条直线叫作互相垂直.其中每一条直线叫作另一条的垂线“垂直”用符号“⊥”表示.如图中,AB与CD垂直(O为垂足),记作AB⊥CD,
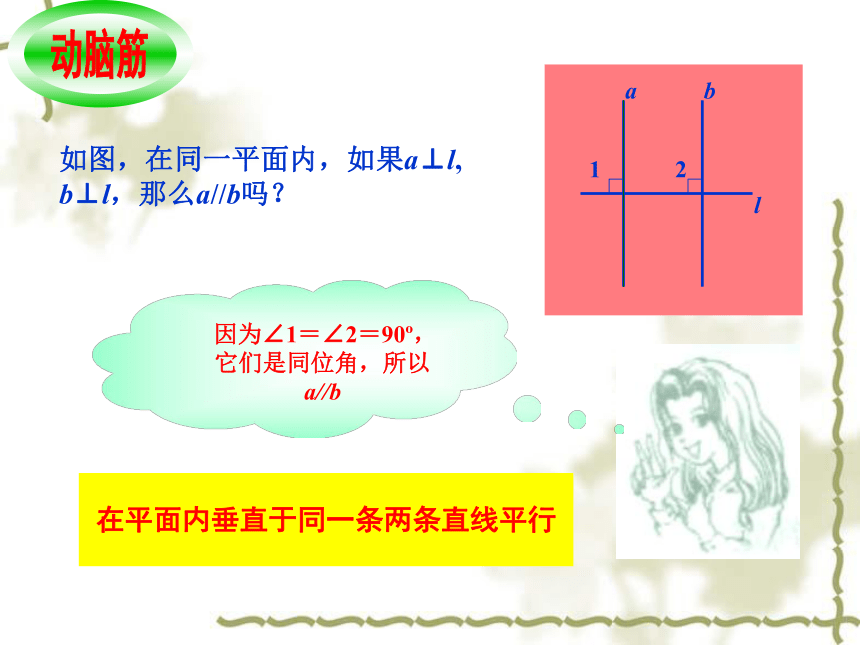
读作AB垂直于CD.如图,在同一平面内,如果a⊥l, b⊥l,那么a//b吗? 因为∠1=∠2=90o,它们是同位角,所以a//b在平面内垂直于同一条两条直线平行如图,设a//b,l⊥a,那么l⊥b吗? 因为l⊥a,所以∠1=90o,因为a//b,所以∠2=∠1=90o,从而l⊥b如图的简易屋架中,BD,AE,HF都垂直于CG,若∠1=60o,求∠2的度数.解 : 因为BD,AE都垂直于
CG,所以BD//AE(在平面内,垂
直于同一条直线的两条直线平行)从而 ∠2=∠1=60o (两直线平行,同位角相等)如图,已知CD⊥AB,∠1=∠2,求∠BFE的度数.解: 因为∠1=∠2,所以
EF//CD (同位角相等,两直线平行).又因为CD⊥AB,所以
EF⊥AB,即∠BFE=90o1.如图,直线AB,CD相交于O,EO⊥CD, ∠BOE=60o,求∠AOC的度数.解:∵ EO⊥CD∴ ∠EOD=90°又 ∠BOE+∠BOD=∠EOD=90°∴ ∠BOD=90°-∠BOE=90°-60°=30°又 ∠BOD=∠AOC∴ ∠AOC=30°ABCD2.如图,AB⊥AD,CD⊥AD,∠B=56o,求∠C解: ∵ AB⊥ADCD⊥AD∴ DC∥AB∴ ∠B+∠C=180°∠C=180°-∠B=180°-56°=124°
读作AB垂直于CD.如图,在同一平面内,如果a⊥l, b⊥l,那么a//b吗? 因为∠1=∠2=90o,它们是同位角,所以a//b在平面内垂直于同一条两条直线平行如图,设a//b,l⊥a,那么l⊥b吗? 因为l⊥a,所以∠1=90o,因为a//b,所以∠2=∠1=90o,从而l⊥b如图的简易屋架中,BD,AE,HF都垂直于CG,若∠1=60o,求∠2的度数.解 : 因为BD,AE都垂直于
CG,所以BD//AE(在平面内,垂
直于同一条直线的两条直线平行)从而 ∠2=∠1=60o (两直线平行,同位角相等)如图,已知CD⊥AB,∠1=∠2,求∠BFE的度数.解: 因为∠1=∠2,所以
EF//CD (同位角相等,两直线平行).又因为CD⊥AB,所以
EF⊥AB,即∠BFE=90o1.如图,直线AB,CD相交于O,EO⊥CD, ∠BOE=60o,求∠AOC的度数.解:∵ EO⊥CD∴ ∠EOD=90°又 ∠BOE+∠BOD=∠EOD=90°∴ ∠BOD=90°-∠BOE=90°-60°=30°又 ∠BOD=∠AOC∴ ∠AOC=30°ABCD2.如图,AB⊥AD,CD⊥AD,∠B=56o,求∠C解: ∵ AB⊥ADCD⊥AD∴ DC∥AB∴ ∠B+∠C=180°∠C=180°-∠B=180°-56°=124°
