5.3 三角形
图片预览









文档简介
课件31张PPT。下面请大家仔细观察一组图片,看看它们有什么共同特点下面请大家仔细观察一组图片,看看它们有什么共同特点下面请大家仔细观察一组图片,看看它们有什么共同特点下面请大家仔细观察一组图片,看看它们有什么共同特点下面请大家仔细观察一组图片,看看它们有什么共同特点5.3 三 角 形
请每个同学画出一个三角形,与同伴交流一下,有多少不同的画法?
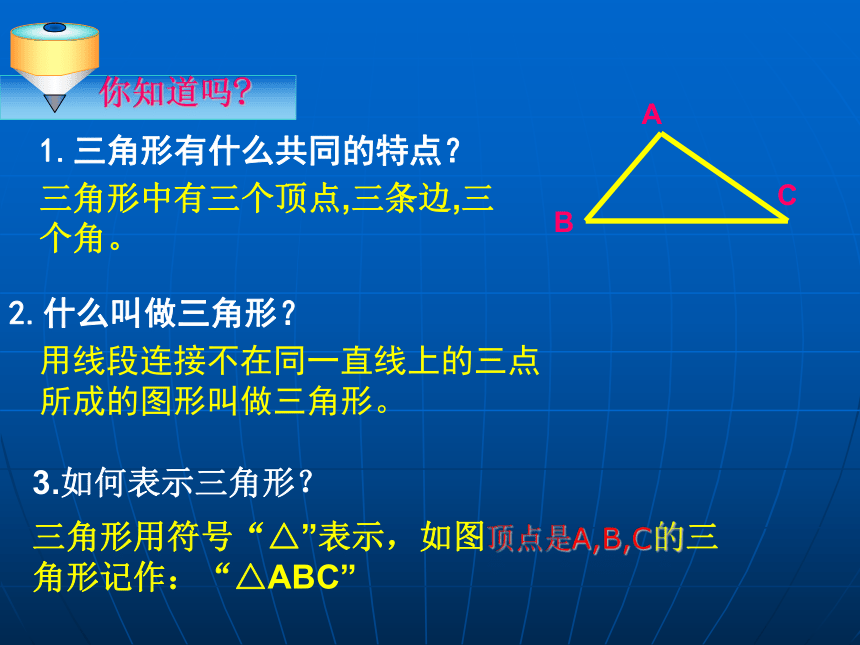
试一试三角形中有三个顶点,三条边,三个角。
1.三角形有什么共同的特点?
用线段连接不在同一直线上的三点所成的图形叫做三角形。2.什么叫做三角形? 3.如何表示三角形?三角形用符号“△”表示,如图顶点是A,B,C的三角形记作:“△ABC”
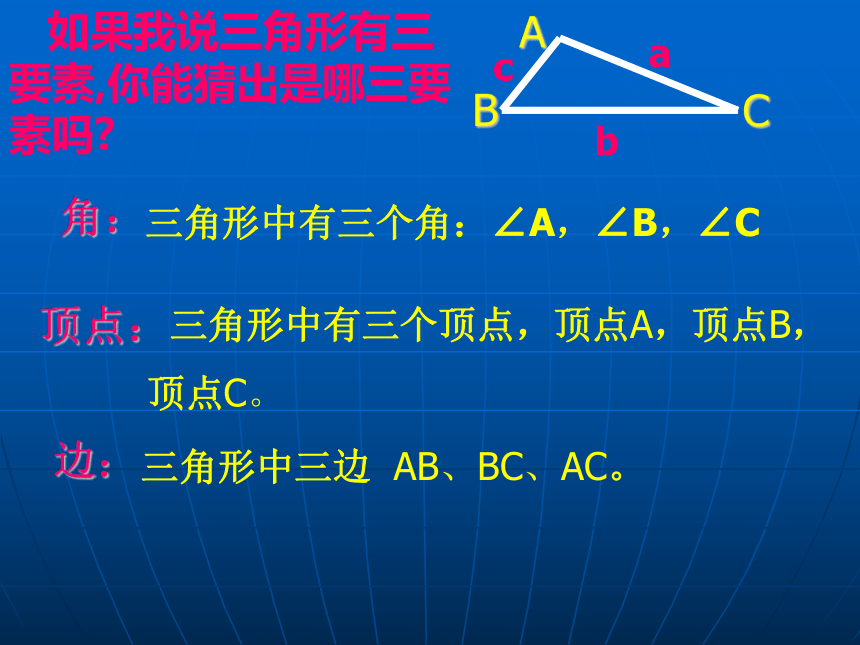
∠A ,∠B ,∠C叫做三角形的三个内角.
线段AB、 BC 、CA叫做三角形的边.(单独存在的三角形的三边有时也用小写字母表示,如: △ABC的三边也可用a、b 、c来表示,顶点A所对的边BC用a表示,边BC 边CA分别用b、 c来表示).
边:三角形中三边 AB、BC、AC。角:三角形中有三个角:∠A,∠B,∠C顶点: 三角形中有三个顶点,顶点A,顶点B,
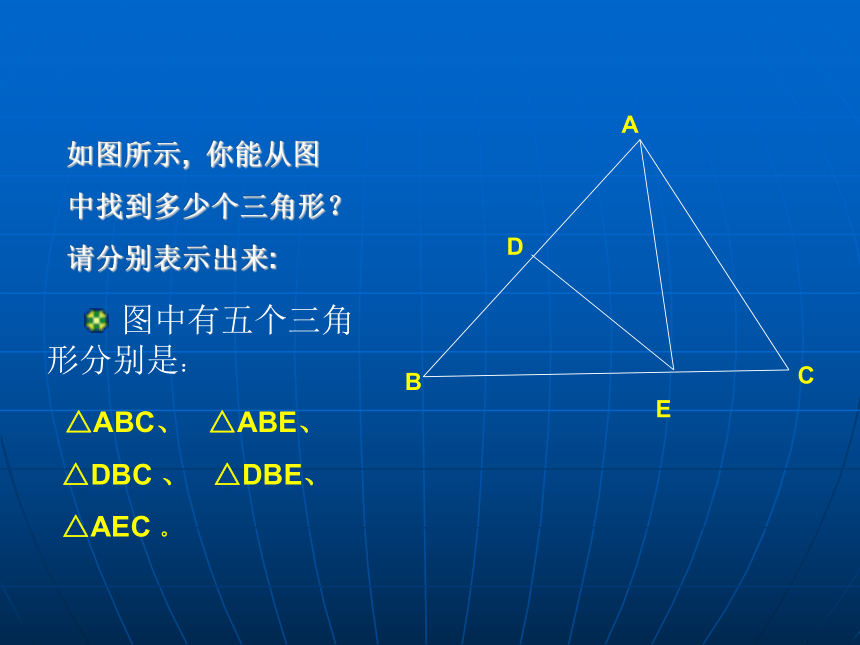
顶点C。ABE CD 图中有五个三角形分别是:
△ABC、 △ABE、
△DBC 、 △DBE、
△AEC 。
如图所示, 你能从图
中找到多少个三角形?
请分别表示出来:
2019/3/10同学们请看好了!下面是小S同学把△ABC中的∠BAC的角平分线给画出来了,这条角平分线与∠BAC的对边相交于D点,此时的线段AD我们怎样命名呢?答案:线段AD是△ABC的∠BAC的角平分线ABDC同学们请看好了!下面是大S同学把△ABC ∠A的对边BC的中点E给找到了, 此时的线段AE我们又怎样命名呢?
答案:线段AE是△ABC的BC边上的中线ACEB同学们请看好了!下面是小M同学过△ABC 的顶点A作边BC的垂线,垂足为F, 此时的线段AF我们又怎样命名呢?
答案:线段AF是△ABC 的BC边上的高ACFB
请同学们猜想一下:
三角形的角平分线,中线,高分别有几条?它们是在三角形内还是在三角形外?
答案:三角形有三条角平分线,三条中线,三条高.三条角平分线和三条中线是在三角形内,而三条高不一定都在三角形内,但至少有一条高是在三角形内.
下面是△ABC ,过顶点A分别作它的角平分线,中线,高,聪明的你一定能作出来,试一试吧!ABC
请以长为1cm、2cm、4cm的三条线段画三角形,试试看,能画出来吗?
这说明:并不是任意的三条线段都可以构成三角形.
探索活动这是世界上最长的跨海大桥杭州湾大桥,请同学们比较从宁波到嘉兴是从桥上直接通过快还是绕杭州再到嘉兴快?为什么?请用规范的几何语言描述
杭 州 湾嘉兴杭州宁波1、这三地(分别用字母A、B、C表示)的地理位置形成了一个三角形区域,如图:利用你发现的规律填空
AB+AC BC
AB+BC AC
AC+BC AB2、在一个三角形中,任意两边之和与第三边的长度有怎样的关系?
为什么?由此你能得到什么结论?ABC 三角形任意两边之和大于第三边
AB+AC﹥BC
AB+BC﹥AC
AC+BC﹥AB利用不等式性质可把这个式子变形得:
BC﹣AB﹤AC AB﹣AC﹤BC AC﹣BC﹤AB3、可推断:三角形任意两边之和与第三边的长度有怎样的关系?为什么?由此你能得到什么结论?
三角形任意两边之差小于第三边
三角形三边的关系三角形两边
的和大于第三边三角形两边
的差小于第三边a-bb-ca-cc
b+c >a
a+c >b
例1:
下列各组数分别是三根小木棒的长度,摆一摆,看看哪组可以拼成三角形.
(1)12cm 7cm 6cm
(2)5cm 6cm 11cm
(3)4cm 10cm 5cm解:(1)因为12﹢7﹥6 ,12﹢6﹥7,7﹢6﹥12满足“任意两边之和大于第三边”,所以这一组能拼成三角形;
(2)因为11 ﹢ 5 ﹥ 6,11 ﹢ 6 ﹥ 5但5 ﹢ 6=11,不满足“任意两边之和大于第三边”,所以这一组不能拼成三角形;
(3)因为4 ﹢ 10 ﹥ 5,4 ﹢ 5﹤10,10 ﹢ 5 ﹥ 4 ,不满足“任意两边之和大于第三边”,所以这一组不能拼成三角形.
判断三条线段能否拼成三角形,可依据:
小﹢小﹥大
大 ﹣小﹤小(大只最长线段,小指较小的两条线段)∠A ,∠B ,∠C叫做三角形
的三个内角.
线段AB、 BC 、CA叫做三
角形的边.(单独存在的三角
形三边有时也用小写字母表
如: △ABC的三边也可用a、
b、c来表示,顶点A所对的
边BC用a表示,边BC、边CA
分别用b、 c来表示).
例2:
有两根长分别是5cm 、 8cm的小木棒,与长度为2cm的木棒能拼成三角形吗?为什么?长度为
13cm的木棒呢?为7cm的木棒呢?
解: (1) 因为2 ﹢ 5 ﹤ 8,所以不能拼成三角形
(2)因为5 ﹢ 8 =13,所以不能拼成三角形
(3)因为5 ﹢ 7 ﹥ 8,所以能拼成三角形
1、指出图中有几个三角形,并分别用符号表示出来BDA答:有6个.分别是△ABC、△ABD、 △ABE 、 △ADE 、 △ADC 、 △AECCE2.比比看谁的反应快!
下列每组数分别是三条线段的长度,用它们能拼成三角形吗?
(1)3cm、4cm、5cm
(2)3cm、12cm、8cm
(3)6cm、6cm、6cm
(4)5.5cm、7.5cm、2.5cm
(5)100cm、200cm、300cm
能组成三角形的有____;
『答案: (1) (3) (4)』
不能组成三角形的有____.
『答案: (2) (5) 』
4.一个等腰三角形的一边长9cm,另一边长4cm,则它的周长是多少?为什么?
提示:既然是等腰三角形,那么另一边的长要么是,要么是9cm.
如果是4cm,那么4 ﹢ 4﹤9cm,这样不满足三角形的三边关系,所以另一边的长只能是9cm,周长就应该是9﹢9﹢4=22cm.
3.一个三角形的两边长分别是2cm、5cm,则第三边长X的取值范围是多少? 分析: X应满足大于5﹣2﹦3cm,小于5 ﹢ 2 ﹦7cm,所以3﹤X﹤7. 小结:三角形两边之和大于第三边三角形两边之差小于第三边 这节课你有那些收获?
有哪些困惑?
1、有下列长度的三条线段,组成三角形的是( )
(A)1㎝,3㎝,5㎝(B)2㎝,4㎝,6㎝
(C)1㎝,2㎝,3㎝(D)2㎝,3㎝,4㎝
2、三角形的三边长分别不3㎝,8㎝,x㎝,且x为整
数,那么x应满足的不等式是_______________,可能
取的值共有________个。
3、△ABC中,AB=14,BC=4x,AC=3x,则x的取
值范围是____________
4、等腰三角形某两边之长分别为6㎝和8㎝,那么周长等
于______________.
再 见
请每个同学画出一个三角形,与同伴交流一下,有多少不同的画法?
试一试三角形中有三个顶点,三条边,三个角。
1.三角形有什么共同的特点?
用线段连接不在同一直线上的三点所成的图形叫做三角形。2.什么叫做三角形? 3.如何表示三角形?三角形用符号“△”表示,如图顶点是A,B,C的三角形记作:“△ABC”
∠A ,∠B ,∠C叫做三角形的三个内角.
线段AB、 BC 、CA叫做三角形的边.(单独存在的三角形的三边有时也用小写字母表示,如: △ABC的三边也可用a、b 、c来表示,顶点A所对的边BC用a表示,边BC 边CA分别用b、 c来表示).
边:三角形中三边 AB、BC、AC。角:三角形中有三个角:∠A,∠B,∠C顶点: 三角形中有三个顶点,顶点A,顶点B,
顶点C。ABE CD 图中有五个三角形分别是:
△ABC、 △ABE、
△DBC 、 △DBE、
△AEC 。
如图所示, 你能从图
中找到多少个三角形?
请分别表示出来:
2019/3/10同学们请看好了!下面是小S同学把△ABC中的∠BAC的角平分线给画出来了,这条角平分线与∠BAC的对边相交于D点,此时的线段AD我们怎样命名呢?答案:线段AD是△ABC的∠BAC的角平分线ABDC同学们请看好了!下面是大S同学把△ABC ∠A的对边BC的中点E给找到了, 此时的线段AE我们又怎样命名呢?
答案:线段AE是△ABC的BC边上的中线ACEB同学们请看好了!下面是小M同学过△ABC 的顶点A作边BC的垂线,垂足为F, 此时的线段AF我们又怎样命名呢?
答案:线段AF是△ABC 的BC边上的高ACFB
请同学们猜想一下:
三角形的角平分线,中线,高分别有几条?它们是在三角形内还是在三角形外?
答案:三角形有三条角平分线,三条中线,三条高.三条角平分线和三条中线是在三角形内,而三条高不一定都在三角形内,但至少有一条高是在三角形内.
下面是△ABC ,过顶点A分别作它的角平分线,中线,高,聪明的你一定能作出来,试一试吧!ABC
请以长为1cm、2cm、4cm的三条线段画三角形,试试看,能画出来吗?
这说明:并不是任意的三条线段都可以构成三角形.
探索活动这是世界上最长的跨海大桥杭州湾大桥,请同学们比较从宁波到嘉兴是从桥上直接通过快还是绕杭州再到嘉兴快?为什么?请用规范的几何语言描述
杭 州 湾嘉兴杭州宁波1、这三地(分别用字母A、B、C表示)的地理位置形成了一个三角形区域,如图:利用你发现的规律填空
AB+AC BC
AB+BC AC
AC+BC AB2、在一个三角形中,任意两边之和与第三边的长度有怎样的关系?
为什么?由此你能得到什么结论?ABC 三角形任意两边之和大于第三边
AB+AC﹥BC
AB+BC﹥AC
AC+BC﹥AB利用不等式性质可把这个式子变形得:
BC﹣AB﹤AC AB﹣AC﹤BC AC﹣BC﹤AB3、可推断:三角形任意两边之和与第三边的长度有怎样的关系?为什么?由此你能得到什么结论?
三角形任意两边之差小于第三边
三角形三边的关系三角形两边
的和大于第三边三角形两边
的差小于第三边a-b
b+c >a
a+c >b
例1:
下列各组数分别是三根小木棒的长度,摆一摆,看看哪组可以拼成三角形.
(1)12cm 7cm 6cm
(2)5cm 6cm 11cm
(3)4cm 10cm 5cm解:(1)因为12﹢7﹥6 ,12﹢6﹥7,7﹢6﹥12满足“任意两边之和大于第三边”,所以这一组能拼成三角形;
(2)因为11 ﹢ 5 ﹥ 6,11 ﹢ 6 ﹥ 5但5 ﹢ 6=11,不满足“任意两边之和大于第三边”,所以这一组不能拼成三角形;
(3)因为4 ﹢ 10 ﹥ 5,4 ﹢ 5﹤10,10 ﹢ 5 ﹥ 4 ,不满足“任意两边之和大于第三边”,所以这一组不能拼成三角形.
判断三条线段能否拼成三角形,可依据:
小﹢小﹥大
大 ﹣小﹤小(大只最长线段,小指较小的两条线段)∠A ,∠B ,∠C叫做三角形
的三个内角.
线段AB、 BC 、CA叫做三
角形的边.(单独存在的三角
形三边有时也用小写字母表
如: △ABC的三边也可用a、
b、c来表示,顶点A所对的
边BC用a表示,边BC、边CA
分别用b、 c来表示).
例2:
有两根长分别是5cm 、 8cm的小木棒,与长度为2cm的木棒能拼成三角形吗?为什么?长度为
13cm的木棒呢?为7cm的木棒呢?
解: (1) 因为2 ﹢ 5 ﹤ 8,所以不能拼成三角形
(2)因为5 ﹢ 8 =13,所以不能拼成三角形
(3)因为5 ﹢ 7 ﹥ 8,所以能拼成三角形
1、指出图中有几个三角形,并分别用符号表示出来BDA答:有6个.分别是△ABC、△ABD、 △ABE 、 △ADE 、 △ADC 、 △AECCE2.比比看谁的反应快!
下列每组数分别是三条线段的长度,用它们能拼成三角形吗?
(1)3cm、4cm、5cm
(2)3cm、12cm、8cm
(3)6cm、6cm、6cm
(4)5.5cm、7.5cm、2.5cm
(5)100cm、200cm、300cm
能组成三角形的有____;
『答案: (1) (3) (4)』
不能组成三角形的有____.
『答案: (2) (5) 』
4.一个等腰三角形的一边长9cm,另一边长4cm,则它的周长是多少?为什么?
提示:既然是等腰三角形,那么另一边的长要么是,要么是9cm.
如果是4cm,那么4 ﹢ 4﹤9cm,这样不满足三角形的三边关系,所以另一边的长只能是9cm,周长就应该是9﹢9﹢4=22cm.
3.一个三角形的两边长分别是2cm、5cm,则第三边长X的取值范围是多少? 分析: X应满足大于5﹣2﹦3cm,小于5 ﹢ 2 ﹦7cm,所以3﹤X﹤7. 小结:三角形两边之和大于第三边三角形两边之差小于第三边 这节课你有那些收获?
有哪些困惑?
1、有下列长度的三条线段,组成三角形的是( )
(A)1㎝,3㎝,5㎝(B)2㎝,4㎝,6㎝
(C)1㎝,2㎝,3㎝(D)2㎝,3㎝,4㎝
2、三角形的三边长分别不3㎝,8㎝,x㎝,且x为整
数,那么x应满足的不等式是_______________,可能
取的值共有________个。
3、△ABC中,AB=14,BC=4x,AC=3x,则x的取
值范围是____________
4、等腰三角形某两边之长分别为6㎝和8㎝,那么周长等
于______________.
再 见
