12.3.1等腰三角形判定
文档属性
| 名称 | 12.3.1等腰三角形判定 |

|
|
| 格式 | rar | ||
| 文件大小 | 308.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-11-07 00:00:00 | ||
图片预览



文档简介
课件15张PPT。12.3.1等腰三角形(2)复习:等腰三角形的性质等腰三角形的两腰相等;
等腰三角形的两个底角相等(简称等边对等角);
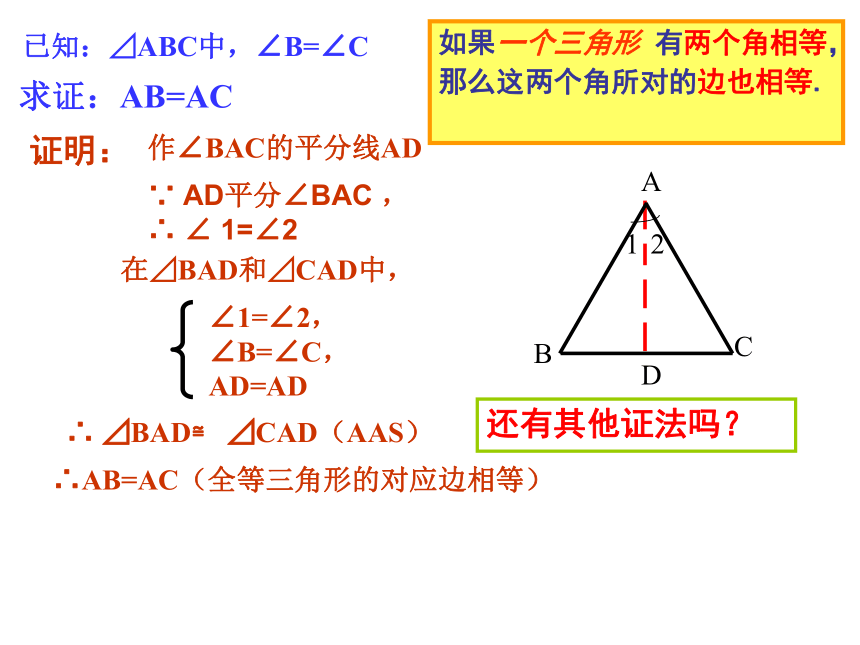
等腰三角形顶角的平分线,底边上的中线,底边上的高互相重合.已知:⊿ABC中,∠B=∠C求证:AB=AC证明:作∠BAC的平分线AD在⊿BAD和⊿CAD中,∠1=∠2,
∠B=∠C,
AD=AD∴ ⊿BAD≌ ⊿CAD(AAS)∴AB=AC(全等三角形的对应边相等)12还有其他证法吗?∵ AD平分∠BAC ,
∴ ∠ 1=∠2如果一个三角形 有两个角相等,那么这两个角所对的边也相等.如果一个三角形有两个角相等,
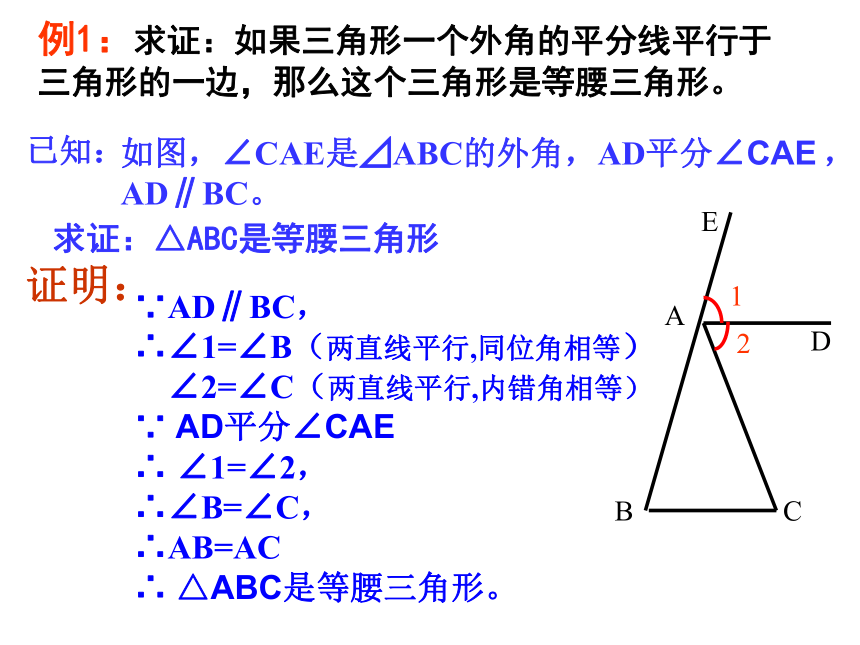
那么这两个角所对的边也相等.简写成”等角对等边”.等腰三角形的判定定理注意: “等角对等边”的前提是一个 三角形例1:求证:如果三角形一个外角的平分线平行于
三角形的一边,那么这个三角形是等腰三角形。求证:△ABC是等腰三角形证明:∵AD∥BC,
∴∠1=∠B(两直线平行,同位角相等)
∠2=∠C(两直线平行,内错角相等)
∵ AD平分∠CAE
∴ ∠1=∠2,
∴∠B=∠C,
∴AB=AC
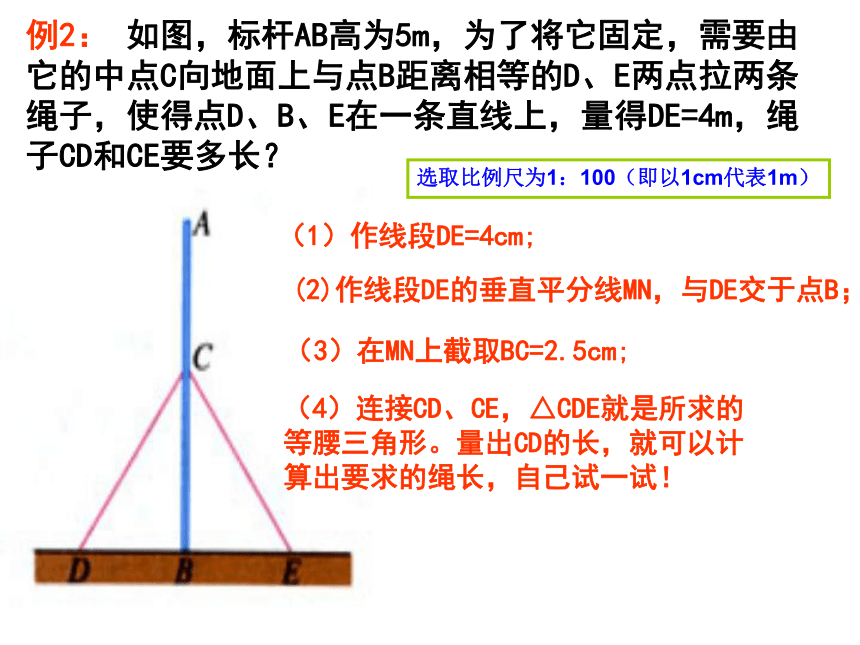
∴ △ABC是等腰三角形。例2: 如图,标杆AB高为5m,为了将它固定,需要由它的中点C向地面上与点B距离相等的D、E两点拉两条绳子,使得点D、B、E在一条直线上,量得DE=4m,绳子CD和CE要多长?选取比例尺为1:100(即以1cm代表1m) (1)作线段DE=4cm; (2)作线段DE的垂直平分线MN,与DE交于点B; (3)在MN上截取BC=2.5cm;(4)连接CD、CE,△CDE就是所求的等腰三角形。量出CD的长,就可以计算出要求的绳长,自己试一试!问题:1.如右图所示△ABC是等腰三角形,AB=AC,倘若一不留心.它的一部分被墨水涂没了,只留下一条底边BC和一个底角∠C.同学们想一想,有没有办法把原来的等腰三角形ABC重新画出来?大家试试看.ABCBC方法一:用角的相等来画.BCA方法二:用过底边中点作垂线的方法来画.BCA请你解决问题2.已知在等腰△ABC中,∠A=36°,∠ B=72°,∠C=72°,请同学们想一想,如何添一条线,将等腰△ABC分成两个等腰三角形?成功后,如何再添一条线,多得到一个等腰三角形?还可以继续吗?只要作∠ B的角平分线即可!
只要再做∠ BDC的角平分线即可!
以下步骤重复下去即可!
如图,在△ABC中,AB=AC, ∠A=36°,你能把△ABC分成三个等腰
三角形吗?(提供两种以上不同的作图方案)ABC动手画一画 1.如图,线段OD的一个端点O在直线a上,以OD为一边画等腰三角形,并且使另一个顶点在直线a上,这样的等腰三角形能画多少个?OD⌒CaEFH小小探索家:2.在正方形ABCD内找一点P,使△PAB、△PBC、△PCD、△PAD都是等腰三角形,这样的P点有几个?在正方形ABCD外呢?
●●●●●BACD●●●●答:在正方形内的P点有5个
在正方形外的P点有4个,如图小小探索家这些点的位置有什么特色呢?已知点A的坐标为(1,-1),在y轴上找一点P,使△POA为等腰三角形.这样的点P共有多少个?探究3P1P2P3P4其中,以OA为腰的三角形有△OAP1、 △OAP2、 △OAP3,
以OA为腰的三角形有△OAP4如图, △ABC中,AB=AC,D为AB上一点,E为AC延长线上一点,且BD=CE,DE交BC于G.求证:DG=EG.思路
因为△GDB和△GEC不全等,所以考虑在△GDB内作出一个与△GEC全等的三角形。★★思考题:
等腰三角形的两个底角相等(简称等边对等角);
等腰三角形顶角的平分线,底边上的中线,底边上的高互相重合.已知:⊿ABC中,∠B=∠C求证:AB=AC证明:作∠BAC的平分线AD在⊿BAD和⊿CAD中,∠1=∠2,
∠B=∠C,
AD=AD∴ ⊿BAD≌ ⊿CAD(AAS)∴AB=AC(全等三角形的对应边相等)12还有其他证法吗?∵ AD平分∠BAC ,
∴ ∠ 1=∠2如果一个三角形 有两个角相等,那么这两个角所对的边也相等.如果一个三角形有两个角相等,
那么这两个角所对的边也相等.简写成”等角对等边”.等腰三角形的判定定理注意: “等角对等边”的前提是一个 三角形例1:求证:如果三角形一个外角的平分线平行于
三角形的一边,那么这个三角形是等腰三角形。求证:△ABC是等腰三角形证明:∵AD∥BC,
∴∠1=∠B(两直线平行,同位角相等)
∠2=∠C(两直线平行,内错角相等)
∵ AD平分∠CAE
∴ ∠1=∠2,
∴∠B=∠C,
∴AB=AC
∴ △ABC是等腰三角形。例2: 如图,标杆AB高为5m,为了将它固定,需要由它的中点C向地面上与点B距离相等的D、E两点拉两条绳子,使得点D、B、E在一条直线上,量得DE=4m,绳子CD和CE要多长?选取比例尺为1:100(即以1cm代表1m) (1)作线段DE=4cm; (2)作线段DE的垂直平分线MN,与DE交于点B; (3)在MN上截取BC=2.5cm;(4)连接CD、CE,△CDE就是所求的等腰三角形。量出CD的长,就可以计算出要求的绳长,自己试一试!问题:1.如右图所示△ABC是等腰三角形,AB=AC,倘若一不留心.它的一部分被墨水涂没了,只留下一条底边BC和一个底角∠C.同学们想一想,有没有办法把原来的等腰三角形ABC重新画出来?大家试试看.ABCBC方法一:用角的相等来画.BCA方法二:用过底边中点作垂线的方法来画.BCA请你解决问题2.已知在等腰△ABC中,∠A=36°,∠ B=72°,∠C=72°,请同学们想一想,如何添一条线,将等腰△ABC分成两个等腰三角形?成功后,如何再添一条线,多得到一个等腰三角形?还可以继续吗?只要作∠ B的角平分线即可!
只要再做∠ BDC的角平分线即可!
以下步骤重复下去即可!
如图,在△ABC中,AB=AC, ∠A=36°,你能把△ABC分成三个等腰
三角形吗?(提供两种以上不同的作图方案)ABC动手画一画 1.如图,线段OD的一个端点O在直线a上,以OD为一边画等腰三角形,并且使另一个顶点在直线a上,这样的等腰三角形能画多少个?OD⌒CaEFH小小探索家:2.在正方形ABCD内找一点P,使△PAB、△PBC、△PCD、△PAD都是等腰三角形,这样的P点有几个?在正方形ABCD外呢?
●●●●●BACD●●●●答:在正方形内的P点有5个
在正方形外的P点有4个,如图小小探索家这些点的位置有什么特色呢?已知点A的坐标为(1,-1),在y轴上找一点P,使△POA为等腰三角形.这样的点P共有多少个?探究3P1P2P3P4其中,以OA为腰的三角形有△OAP1、 △OAP2、 △OAP3,
以OA为腰的三角形有△OAP4如图, △ABC中,AB=AC,D为AB上一点,E为AC延长线上一点,且BD=CE,DE交BC于G.求证:DG=EG.思路
因为△GDB和△GEC不全等,所以考虑在△GDB内作出一个与△GEC全等的三角形。★★思考题:
