2010年慈溪市新分配初中数学教师基本功操练笔试试卷
文档属性
| 名称 | 2010年慈溪市新分配初中数学教师基本功操练笔试试卷 |

|
|
| 格式 | rar | ||
| 文件大小 | 165.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-11-05 09:22:00 | ||
图片预览

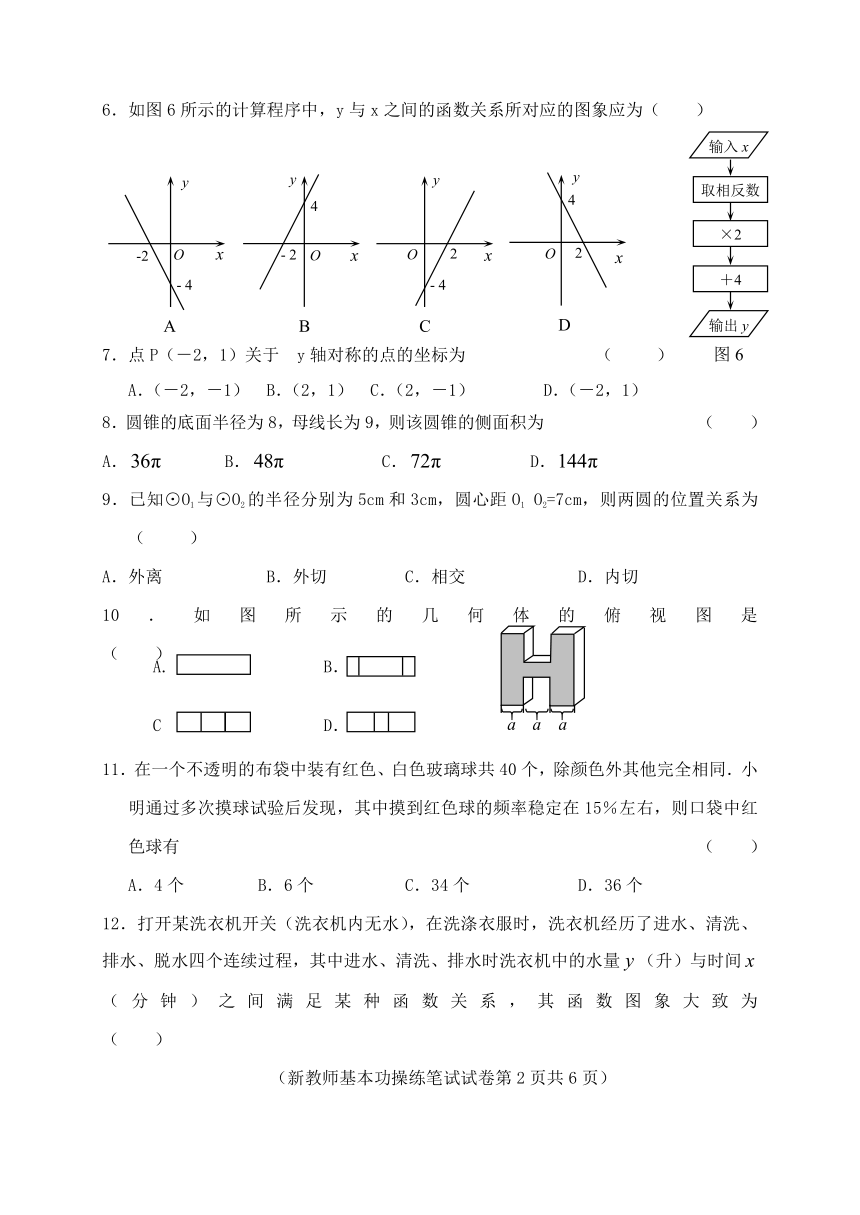
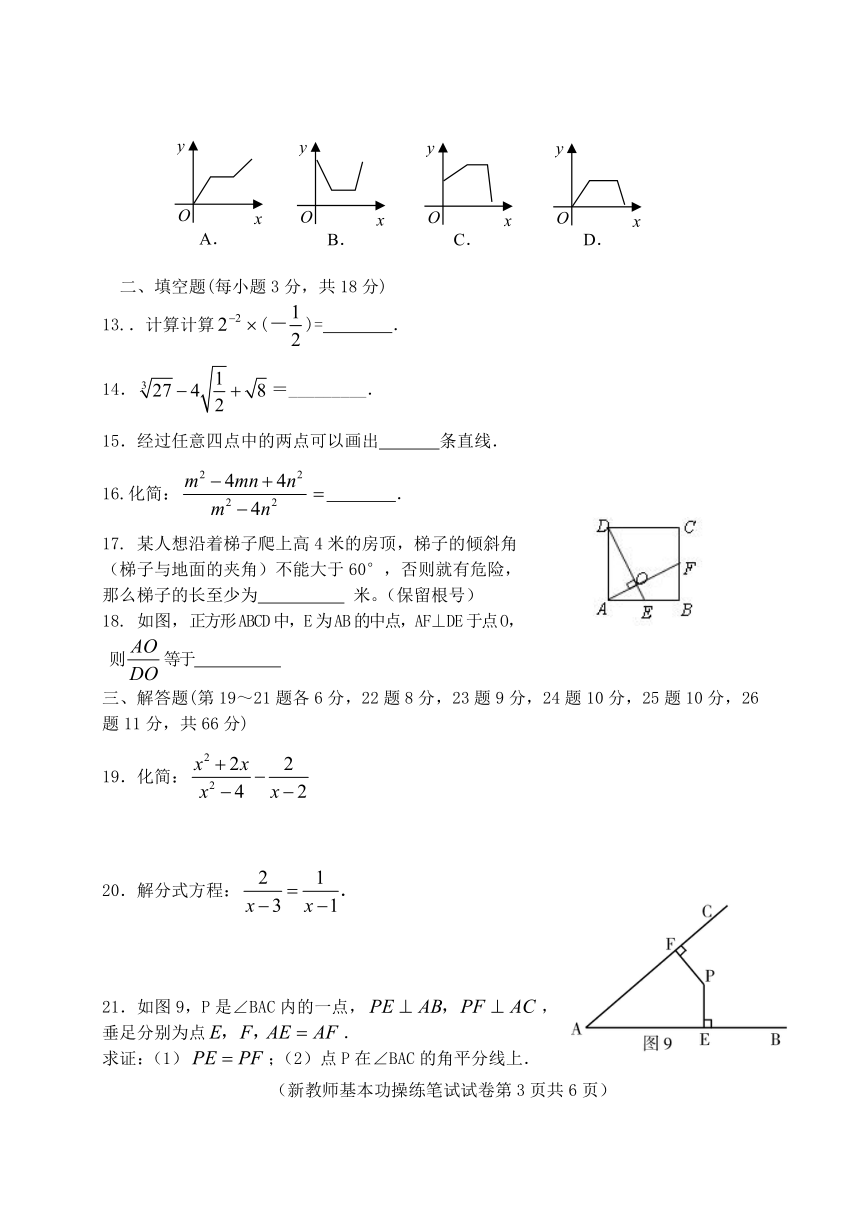


文档简介
2010年慈溪市新分配初中数学教师基本功操练笔试试卷
学校 姓名
(满分:120分 时间120分)
题号 一 二 19 20 21 22 23 24 25 26 总分
得分
一、选择题(每小题3分,共36分,在每小题给出的四个选项中,只有一项符合题目要求)
1. -5的相反数是 ( )
A.5 B. C. D.
2. 伴随着气候变化大会诞生的“碳足迹计算器”最近在网上流行起来。据估算,在某人一年的碳足迹中,一件衣服的碳排放是5.7公斤。照此计算,如果慈溪100万人春节每人少买一件衣服,可为成都减少碳排放570万吨。用科学计数法应记为: ( )
A. 吨 B. 吨 C. 吨 D. 吨
3.计算的结果是 ( )
A. B. C. D.
4.如图,半圆的直径AB=10cm,把弓形AD沿直线AD对折,交直径AB于点C’,若AC’=6cm,则AD的长为( )
A. B. C. D.
5.下列说法中,正确的是 ( )
A.“明天降雨的概率是80%”表示明天有80%的时间降雨
B.“抛一枚硬币正面朝上的概率是0.5”表示每抛硬币2次就有1次出现正面朝上
C.“彩票中奖的概率是1%”表示买100张彩票一定有1张会中奖
D.在同一年出生的367名学生中,至少有两人的生日是同一天
(新教师基本功操练笔试试卷第1页共6页)
6.如图6所示的计算程序中,y与x之间的函数关系所对应的图象应为( )
7.点P(-2,1)关于 y轴对称的点的坐标为 ( )
A.(-2,-1) B.(2,1) C.(2,-1) D.(-2,1)
8.圆锥的底面半径为8,母线长为9,则该圆锥的侧面积为 ( )
A. B. C. D.
9.已知⊙O1与⊙O2的半径分别为5cm和3cm,圆心距O1 O2=7cm,则两圆的位置关系为( )
A.外离 B.外切 C.相交 D.内切
10.如图所示的几何体的俯视图是 ( )
11.在一个不透明的布袋中装有红色、白色玻璃球共40个,除颜色外其他完全相同.小明通过多次摸球试验后发现,其中摸到红色球的频率稳定在15%左右,则口袋中红色球有 ( )
A.4个 B.6个 C.34个 D.36个
12.打开某洗衣机开关(洗衣机内无水),在洗涤衣服时,洗衣机经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量(升)与时间(分钟)之间满足某种函数关系,其函数图象大致为 ( )
(新教师基本功操练笔试试卷第2页共6页)
二、填空题(每小题3分,共18分)
13..计算计算()= .
14.=_________.
15.经过任意四点中的两点可以画出 条直线.
16.化简: .
17. 某人想沿着梯子爬上高4米的房顶,梯子的倾斜角
(梯子与地面的夹角)不能大于60°,否则就有危险,
那么梯子的长至少为 米。(保留根号)
18. 如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O,
则等于
三、解答题(第19~21题各6分,22题8分,23题9分,24题10分,25题10分,26题11分,共66分)
19.化简:
20.解分式方程:
21.如图9,P是∠BAC内的一点,,
垂足分别为点.
求证:(1);(2)点P在∠BAC的角平分线上.
(新教师基本功操练笔试试卷第3页共6页)
22.某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费.某顾客刚好消费200元.
(1)该顾客至少可得到 元购物券,至多可得到 元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
23..已知:如图所示的两条抛物线的解析式分别是
,(其中为常数,且).
(1)请写出三条与上述抛物线有关的不同类型的结论;
(2)当时,设与轴分别交于M,N两点(M在N的左边),与轴分别交于E,F两点(E在F的左边),观察M,N,E,F四点坐标,请写出一个你所得到的正确结论,并说明理由;
(3)设上述两条抛物线相交于A,B两点,直线都垂直于轴,分别经过A,B两点,在直线之间,且与两条抛物线分别交于C,D两点,求线段CD的最大值.
24.如图,在Rt△ABC中,∠ABC=90°,D是AC的中点,⊙O经过A、B、D三点,CB的延长线交⊙O于点E.(1)求证AE=CE;
(新教师基本功操练笔试试卷第4页共6页)
(2)EF与⊙O相切于点E,交AC的延长线于点F,若CD=CF=2cm,求⊙O的直径;
(3)若 (n>0),求sin∠CAB.
25.某股份有限公司根据公司实际情况,对本公司职工实行内部医疗公积金制度,公司规定:
(一)每位职工在年初需缴纳医疗公积金元;
(二)职工个人当年治病花费的医疗费年底按表1的办法分段处理:
表1
分段方式 处理方法
不超过150元(含150元) 全部由个人承担
超过150元,不超过10000元(不含150元,含10000元)的部分 个人承担n%,剩余部分由公司承担
超过10000元(不含10000元)的部分 全部由公司承担
设一职工当年治病花费的医疗费为元,他个人实际承担的费用(包括医疗费中个人承担的部分和缴纳的医疗公积金元)为元.
(1)由表1可知,当时,;那么,当时, ;(用含的方式表示)
(2)该公司职员小陈和大李2007年治病花费的医疗费和他们个人实际承担的费用如表2:
(新教师基本功操练笔试试卷第5页共6页)
表2
职工 治病花费的医疗费(元) 个人实际承担的费用(元)
小陈 300 280
大李 500 320
请根据表2中的信息,求的值,并求出当时,关于函数解析式;
(3)该公司职工个人一年因病实际承担费用最多只需要多少元?(直接写出结果)
26.如图,在平面直角坐标系中,点,点A,B分别在x轴,
y轴的正半轴上,且满足.
(1)求点A,点B的坐标.
(2)若点P从C点出发,以每秒1个
单位的速度沿射线CB运动,连结AP.
设的面积为S,点P的运动时
间为秒,求S与的函数关系式,并写出自变量的取值范围.
(3)在(2)的条件下,是否存在点P,使以点为顶点的三角形与相似?若存在,请直接写出点的坐标;若不存在,请说明理由.
(教师基本功操练笔试试卷第2页共6页)
参考答案
一、选择题(每小题3分,共36分)
题号 l 2 3 4 5 6 7 8 9 10 1 l 12
答 案 A C B A D D B C C C B D
二、填空题(每小题3分,共18分)
题号 13 14 15 16 17 18
答案 3 1或4或6 m-2n 1:2
三、解答题(共66分)
注:l.阅卷时应按步计分,每步只设整分;
2.如有其它解法,只要正确,都可参照评分标准,各步相应给分
19.解:原式= (2分)
= (4分)
=1. (6分)
20.解分式方程:
解:去分母得: (2分)
解得 (4分)
检验是原方程的解 (5分)
所以,原方程的解为 (6分)
21.证明:(1)如图1,连结AP,
∴∠AEP=∠AFP= (1分)
又AE=AF,AP=AP, (2分)
∴Rt△AEP≌Rt△AFP,∴PE=PF. (3分)
(2)∵Rt△AEP≌Rt△AFP,
∴∠EAP=∠FAP, (4分)
∴AP是∠BAC的角平分线,
故点P在∠BAC的角平分线上 (6分)
22.解:(1)10,50 (2分)
(2)解:解法一(树状图):
(6分)
从上图可以看出,共有12种可能结果,其中大于或等于30元共有8种可能结果,因此(不低于30元)= (8分)
解法二(列表法):
第一次第二次 0 10 20 30
0 10 20 30
10 10 30 40
20 20 30 50
30 30 40 50
(以下过程同“解法一”)
23.(1)解:答案不唯一,只要合理均可.例如:
①抛物线开口向下,或抛物线开口向上;
②抛物线的对称轴是,或抛物线的对称轴是;
③抛物线经过点,或抛物线经过点;
④抛物线与的形状相同,但开口方向相反;
⑤抛物线与都与轴有两个交点;
⑥抛物线经过点或抛物线经过点;
等等. (3分)
(2)当时,,令,
解得. (4分)
,令,解得. (5分)
①点与点对称,点与点对称;
②四点横坐标的代数和为0;
③(或). (6分)
(3),
抛物线开口向下,抛物线开口向上. (7分)
根据题意,得. (8分)
当时,的最大值是2. (9分)
说明:1.第(1)问每写对一条得1分;
2.第(2)问中,①②③任意写对一条得1分;其它结论参照给分.
24. (本小题满分10分)
HYPERLINK "http://www./" 证明:(1)连接DE,∵∠ABC=90°∴∠ABE=90°,
∴AE是⊙O直径. (1分)
∴∠ADE=90°,∴DE⊥AC. (2分)
又∵D是AC的中点,∴DE是AC的垂直平分线.
∴AE=CE. (3分)
(2)在△ADE和△EFA中,
∵∠ADE=∠AEF=90°,∠DAE=∠FAE,
∴△ADE∽△EFA. (4分)
∴,
∴. (5分)
∴AE=2cm. (6分)
(3) ∵AE是⊙O直径,EF是⊙O的切线,∴∠ADE=∠AEF=90°,
∴Rt△ADE∽Rt△EDF. ∴. (7分)
∵,AD=CD,∴CF=nCD,∴DF=(1+n)CD, ∴DE=CD. (8分)
在Rt△CDE中,CE=CD+DE=CD+(CD) =(n+2)CD.
∴CE=CD. (9分)
∵∠CAB=∠DEC,∴sin∠CAB=sin∠DEC ===. (10分)
25.解:(1) 3分
(2)由表2知,小陈和大李的医疗费超过150元而小于10000元,因此有:
(5分)
解得: (6分)
.
. (8分)
(3)个人实际承担的费用最多只需2220元. (10分)
26.解:(1) HYPERLINK "http://www." EMBED Equation.DSMT4
, (1分)
, (2分)
点,点分别在轴,轴的正半轴上
(3分)
(2)求得 (4分)
(每个解析式各1分,两个取值范围共1分) (7分)
(3);;; (11分)
注:本卷中所有题目,若由其它方法得出正确结论,酌情给分.
和
第二次
第一次
40
30
50
10
0
30
20
50
30
20
20
30
10
0
40
30
10
30
20
0
10
30
20
10
30
20
10
0
取相反数
×2
+4
图6
输入x
输出y
O
y
x
-2
- 4
A
D
C
B
O
4
2
y
O
2
- 4
y
x
O
4
- 2
y
x
x
A.
B.
C
D.
a
a
a
O
x
y
O
x
y
O
x
y
O
x
y
A.
B.
C.
D.
PAGE
学校 姓名
(满分:120分 时间120分)
题号 一 二 19 20 21 22 23 24 25 26 总分
得分
一、选择题(每小题3分,共36分,在每小题给出的四个选项中,只有一项符合题目要求)
1. -5的相反数是 ( )
A.5 B. C. D.
2. 伴随着气候变化大会诞生的“碳足迹计算器”最近在网上流行起来。据估算,在某人一年的碳足迹中,一件衣服的碳排放是5.7公斤。照此计算,如果慈溪100万人春节每人少买一件衣服,可为成都减少碳排放570万吨。用科学计数法应记为: ( )
A. 吨 B. 吨 C. 吨 D. 吨
3.计算的结果是 ( )
A. B. C. D.
4.如图,半圆的直径AB=10cm,把弓形AD沿直线AD对折,交直径AB于点C’,若AC’=6cm,则AD的长为( )
A. B. C. D.
5.下列说法中,正确的是 ( )
A.“明天降雨的概率是80%”表示明天有80%的时间降雨
B.“抛一枚硬币正面朝上的概率是0.5”表示每抛硬币2次就有1次出现正面朝上
C.“彩票中奖的概率是1%”表示买100张彩票一定有1张会中奖
D.在同一年出生的367名学生中,至少有两人的生日是同一天
(新教师基本功操练笔试试卷第1页共6页)
6.如图6所示的计算程序中,y与x之间的函数关系所对应的图象应为( )
7.点P(-2,1)关于 y轴对称的点的坐标为 ( )
A.(-2,-1) B.(2,1) C.(2,-1) D.(-2,1)
8.圆锥的底面半径为8,母线长为9,则该圆锥的侧面积为 ( )
A. B. C. D.
9.已知⊙O1与⊙O2的半径分别为5cm和3cm,圆心距O1 O2=7cm,则两圆的位置关系为( )
A.外离 B.外切 C.相交 D.内切
10.如图所示的几何体的俯视图是 ( )
11.在一个不透明的布袋中装有红色、白色玻璃球共40个,除颜色外其他完全相同.小明通过多次摸球试验后发现,其中摸到红色球的频率稳定在15%左右,则口袋中红色球有 ( )
A.4个 B.6个 C.34个 D.36个
12.打开某洗衣机开关(洗衣机内无水),在洗涤衣服时,洗衣机经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量(升)与时间(分钟)之间满足某种函数关系,其函数图象大致为 ( )
(新教师基本功操练笔试试卷第2页共6页)
二、填空题(每小题3分,共18分)
13..计算计算()= .
14.=_________.
15.经过任意四点中的两点可以画出 条直线.
16.化简: .
17. 某人想沿着梯子爬上高4米的房顶,梯子的倾斜角
(梯子与地面的夹角)不能大于60°,否则就有危险,
那么梯子的长至少为 米。(保留根号)
18. 如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O,
则等于
三、解答题(第19~21题各6分,22题8分,23题9分,24题10分,25题10分,26题11分,共66分)
19.化简:
20.解分式方程:
21.如图9,P是∠BAC内的一点,,
垂足分别为点.
求证:(1);(2)点P在∠BAC的角平分线上.
(新教师基本功操练笔试试卷第3页共6页)
22.某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费.某顾客刚好消费200元.
(1)该顾客至少可得到 元购物券,至多可得到 元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
23..已知:如图所示的两条抛物线的解析式分别是
,(其中为常数,且).
(1)请写出三条与上述抛物线有关的不同类型的结论;
(2)当时,设与轴分别交于M,N两点(M在N的左边),与轴分别交于E,F两点(E在F的左边),观察M,N,E,F四点坐标,请写出一个你所得到的正确结论,并说明理由;
(3)设上述两条抛物线相交于A,B两点,直线都垂直于轴,分别经过A,B两点,在直线之间,且与两条抛物线分别交于C,D两点,求线段CD的最大值.
24.如图,在Rt△ABC中,∠ABC=90°,D是AC的中点,⊙O经过A、B、D三点,CB的延长线交⊙O于点E.(1)求证AE=CE;
(新教师基本功操练笔试试卷第4页共6页)
(2)EF与⊙O相切于点E,交AC的延长线于点F,若CD=CF=2cm,求⊙O的直径;
(3)若 (n>0),求sin∠CAB.
25.某股份有限公司根据公司实际情况,对本公司职工实行内部医疗公积金制度,公司规定:
(一)每位职工在年初需缴纳医疗公积金元;
(二)职工个人当年治病花费的医疗费年底按表1的办法分段处理:
表1
分段方式 处理方法
不超过150元(含150元) 全部由个人承担
超过150元,不超过10000元(不含150元,含10000元)的部分 个人承担n%,剩余部分由公司承担
超过10000元(不含10000元)的部分 全部由公司承担
设一职工当年治病花费的医疗费为元,他个人实际承担的费用(包括医疗费中个人承担的部分和缴纳的医疗公积金元)为元.
(1)由表1可知,当时,;那么,当时, ;(用含的方式表示)
(2)该公司职员小陈和大李2007年治病花费的医疗费和他们个人实际承担的费用如表2:
(新教师基本功操练笔试试卷第5页共6页)
表2
职工 治病花费的医疗费(元) 个人实际承担的费用(元)
小陈 300 280
大李 500 320
请根据表2中的信息,求的值,并求出当时,关于函数解析式;
(3)该公司职工个人一年因病实际承担费用最多只需要多少元?(直接写出结果)
26.如图,在平面直角坐标系中,点,点A,B分别在x轴,
y轴的正半轴上,且满足.
(1)求点A,点B的坐标.
(2)若点P从C点出发,以每秒1个
单位的速度沿射线CB运动,连结AP.
设的面积为S,点P的运动时
间为秒,求S与的函数关系式,并写出自变量的取值范围.
(3)在(2)的条件下,是否存在点P,使以点为顶点的三角形与相似?若存在,请直接写出点的坐标;若不存在,请说明理由.
(教师基本功操练笔试试卷第2页共6页)
参考答案
一、选择题(每小题3分,共36分)
题号 l 2 3 4 5 6 7 8 9 10 1 l 12
答 案 A C B A D D B C C C B D
二、填空题(每小题3分,共18分)
题号 13 14 15 16 17 18
答案 3 1或4或6 m-2n 1:2
三、解答题(共66分)
注:l.阅卷时应按步计分,每步只设整分;
2.如有其它解法,只要正确,都可参照评分标准,各步相应给分
19.解:原式= (2分)
= (4分)
=1. (6分)
20.解分式方程:
解:去分母得: (2分)
解得 (4分)
检验是原方程的解 (5分)
所以,原方程的解为 (6分)
21.证明:(1)如图1,连结AP,
∴∠AEP=∠AFP= (1分)
又AE=AF,AP=AP, (2分)
∴Rt△AEP≌Rt△AFP,∴PE=PF. (3分)
(2)∵Rt△AEP≌Rt△AFP,
∴∠EAP=∠FAP, (4分)
∴AP是∠BAC的角平分线,
故点P在∠BAC的角平分线上 (6分)
22.解:(1)10,50 (2分)
(2)解:解法一(树状图):
(6分)
从上图可以看出,共有12种可能结果,其中大于或等于30元共有8种可能结果,因此(不低于30元)= (8分)
解法二(列表法):
第一次第二次 0 10 20 30
0 10 20 30
10 10 30 40
20 20 30 50
30 30 40 50
(以下过程同“解法一”)
23.(1)解:答案不唯一,只要合理均可.例如:
①抛物线开口向下,或抛物线开口向上;
②抛物线的对称轴是,或抛物线的对称轴是;
③抛物线经过点,或抛物线经过点;
④抛物线与的形状相同,但开口方向相反;
⑤抛物线与都与轴有两个交点;
⑥抛物线经过点或抛物线经过点;
等等. (3分)
(2)当时,,令,
解得. (4分)
,令,解得. (5分)
①点与点对称,点与点对称;
②四点横坐标的代数和为0;
③(或). (6分)
(3),
抛物线开口向下,抛物线开口向上. (7分)
根据题意,得. (8分)
当时,的最大值是2. (9分)
说明:1.第(1)问每写对一条得1分;
2.第(2)问中,①②③任意写对一条得1分;其它结论参照给分.
24. (本小题满分10分)
HYPERLINK "http://www./" 证明:(1)连接DE,∵∠ABC=90°∴∠ABE=90°,
∴AE是⊙O直径. (1分)
∴∠ADE=90°,∴DE⊥AC. (2分)
又∵D是AC的中点,∴DE是AC的垂直平分线.
∴AE=CE. (3分)
(2)在△ADE和△EFA中,
∵∠ADE=∠AEF=90°,∠DAE=∠FAE,
∴△ADE∽△EFA. (4分)
∴,
∴. (5分)
∴AE=2cm. (6分)
(3) ∵AE是⊙O直径,EF是⊙O的切线,∴∠ADE=∠AEF=90°,
∴Rt△ADE∽Rt△EDF. ∴. (7分)
∵,AD=CD,∴CF=nCD,∴DF=(1+n)CD, ∴DE=CD. (8分)
在Rt△CDE中,CE=CD+DE=CD+(CD) =(n+2)CD.
∴CE=CD. (9分)
∵∠CAB=∠DEC,∴sin∠CAB=sin∠DEC ===. (10分)
25.解:(1) 3分
(2)由表2知,小陈和大李的医疗费超过150元而小于10000元,因此有:
(5分)
解得: (6分)
.
. (8分)
(3)个人实际承担的费用最多只需2220元. (10分)
26.解:(1) HYPERLINK "http://www." EMBED Equation.DSMT4
, (1分)
, (2分)
点,点分别在轴,轴的正半轴上
(3分)
(2)求得 (4分)
(每个解析式各1分,两个取值范围共1分) (7分)
(3);;; (11分)
注:本卷中所有题目,若由其它方法得出正确结论,酌情给分.
和
第二次
第一次
40
30
50
10
0
30
20
50
30
20
20
30
10
0
40
30
10
30
20
0
10
30
20
10
30
20
10
0
取相反数
×2
+4
图6
输入x
输出y
O
y
x
-2
- 4
A
D
C
B
O
4
2
y
O
2
- 4
y
x
O
4
- 2
y
x
x
A.
B.
C
D.
a
a
a
O
x
y
O
x
y
O
x
y
O
x
y
A.
B.
C.
D.
PAGE
同课章节目录
