13.3实数(1)
图片预览








文档简介
课件23张PPT。13.3实数
(1)龙湾慈云中学 吴利春义务教育课程标准实验教科书(人教版)毕达哥拉斯(Pythagoras,约公元前580——前500年),古希腊数学家,毕达哥斯学派的主要代表人物. 数学小史
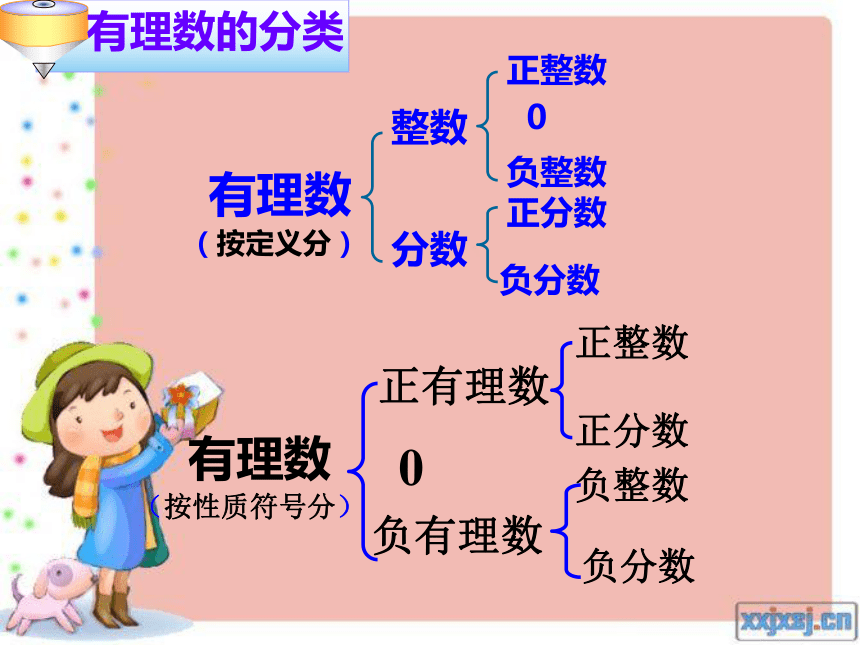
这是古希腊著名的数学家毕达哥拉斯,他在意大利南部的克罗托那建立了一个秘密组织,形成了“毕达哥拉斯学派”,这个学派对数学发展有重要的贡献,著名的勾股定理就是这个学派智慧的结晶.毕达哥拉斯说:“世界上只有整数和分数,除此之外就再也没有什么别的数了!”同学们,你们赞成这位数学家的说法吗?0.612,53,,847,0,2--8 ………有理数整数分数正整数负整数0正分数负分数正有理数负有理数0有理数的分类(按定义分)有理数(按性质符号分) 使用计算器计算,把下列有理数写成小数的形式,你有什么发现?3 = 3.0, 事实上,任何一个有理数都可以写成有限小数或无限循环小数的形式. 反过来,任何_______ ___________有限小数 无限循环小数也都是有理数.或同学们,除了有限小数和无限循环小数,还有其它类型的小数吗?无限不循环小数把下列各数写成小数的形式:无限不循环小数1.41421356237309504880168… 你能举出一些无理数吗?1.73205080756887729352744…
3.1415926535897932384626 …无限不循环小数叫做无理数.
无理数也有正负之分,正无理数:
负无理数:活动1无理数的分类例如:练习:判断下列数哪些是有理数?哪些是无理数? 有理数是: 无理数是: , , , , 1.圆周率 及一些含有 的数;2.开不尽方的数;3.有一定的规律,但不循环的无限小数.无理数的特征:无理数的特征……注意:带根号的数不一定是无理数1.圆周率 及一些含有 的数;2.开不尽方的数;3.有一定的规律,但不循环的无限小数. 有理数集合 无理数集合有理数和无理数统称实数.学以致用实数的定义(一)按定义分类实数的分类(二)按性质符号分类实数的分类判断———看谁最快最准! 1.实数不是有理数就是无理数。( )2.无理数都是无限不循环小数。( )4.无理数都是无限小数。( ) 3.带根号的数都是无理数。( ) 5.无理数一定都带根号。( )××6.两个无理数之和一定是无理数。( )×7.两个无理数之积不一定是无理数。( ) 我是神枪手 如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上一点从原点到达O′点,则点O′的坐标为多少?无理数 可以用数轴上的点来表示.O′问题2.你能在数轴上表示出 吗?问题1.你能在数轴上表示出π吗?OO′=π O′的坐标是π O直径为1的圆(1)如下图,以单位长度为边长画一个正方形,以原点为圆心,正方形对角线为半径画弧,与正、负半轴的交点分别为点A和点B,数轴上A点和B点对应的数是什么? (2)如果将所有有理数都标到数轴上,那么数轴 填满吗?BA每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一点都表示一个实数。C数轴上的点有些
表示有理数,有
些表示无理数.11实数与数轴上的点是一一对应的。事实上,每一个无理数都可以用数轴上的一个点来表示出来。问题3.你能在平面直角坐标系中描出点( ,1)吗?( ,1)有序实数对xy ★平面直角坐标系中的点与有序实数对之间也是一 一对应的.巩固提高1、(1)请将数轴上是各点与下列实数对应起来:ABCDE 3(2)比较它们的大小(用“<”号连接)在数轴上表示的两个实数,右边的数总比左边的数大。3、在数轴上与原点的距离是 的点所表示的数是 。巩固提高4、在数轴上距离表示-2的点是 个
单位长度的数是 。2、设 对应数轴上的点是A, 对应数轴上的点是B,那么A、B间的距离是 。使我感触最深的是……
我学会了……
我感到困难的是……
我想我将…… 小结交流通过这节课的学习说说你的收获:你学会了吗?有理数无理数分数整数有限小数或
无限循环小数无限不循环小数实数
(按定义分)归纳总结★实数和数轴上的点是一一对应的. ★有序实数对和平面直角坐标系中的点是一 一对应的.作业课时作业:第2题课后练习: 第1题课本P86:习题13.3
课外学习:阅读与思考课本P88的材料挑战的相反数
的绝对值 在数学天地里,重要的不是我们知道什么,而是我们怎么知道—— 毕达哥拉斯结束寄语再见
(1)龙湾慈云中学 吴利春义务教育课程标准实验教科书(人教版)毕达哥拉斯(Pythagoras,约公元前580——前500年),古希腊数学家,毕达哥斯学派的主要代表人物. 数学小史
这是古希腊著名的数学家毕达哥拉斯,他在意大利南部的克罗托那建立了一个秘密组织,形成了“毕达哥拉斯学派”,这个学派对数学发展有重要的贡献,著名的勾股定理就是这个学派智慧的结晶.毕达哥拉斯说:“世界上只有整数和分数,除此之外就再也没有什么别的数了!”同学们,你们赞成这位数学家的说法吗?0.612,53,,847,0,2--8 ………有理数整数分数正整数负整数0正分数负分数正有理数负有理数0有理数的分类(按定义分)有理数(按性质符号分) 使用计算器计算,把下列有理数写成小数的形式,你有什么发现?3 = 3.0, 事实上,任何一个有理数都可以写成有限小数或无限循环小数的形式. 反过来,任何_______ ___________有限小数 无限循环小数也都是有理数.或同学们,除了有限小数和无限循环小数,还有其它类型的小数吗?无限不循环小数把下列各数写成小数的形式:无限不循环小数1.41421356237309504880168… 你能举出一些无理数吗?1.73205080756887729352744…
3.1415926535897932384626 …无限不循环小数叫做无理数.
无理数也有正负之分,正无理数:
负无理数:活动1无理数的分类例如:练习:判断下列数哪些是有理数?哪些是无理数? 有理数是: 无理数是: , , , , 1.圆周率 及一些含有 的数;2.开不尽方的数;3.有一定的规律,但不循环的无限小数.无理数的特征:无理数的特征……注意:带根号的数不一定是无理数1.圆周率 及一些含有 的数;2.开不尽方的数;3.有一定的规律,但不循环的无限小数. 有理数集合 无理数集合有理数和无理数统称实数.学以致用实数的定义(一)按定义分类实数的分类(二)按性质符号分类实数的分类判断———看谁最快最准! 1.实数不是有理数就是无理数。( )2.无理数都是无限不循环小数。( )4.无理数都是无限小数。( ) 3.带根号的数都是无理数。( ) 5.无理数一定都带根号。( )××6.两个无理数之和一定是无理数。( )×7.两个无理数之积不一定是无理数。( ) 我是神枪手 如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上一点从原点到达O′点,则点O′的坐标为多少?无理数 可以用数轴上的点来表示.O′问题2.你能在数轴上表示出 吗?问题1.你能在数轴上表示出π吗?OO′=π O′的坐标是π O直径为1的圆(1)如下图,以单位长度为边长画一个正方形,以原点为圆心,正方形对角线为半径画弧,与正、负半轴的交点分别为点A和点B,数轴上A点和B点对应的数是什么? (2)如果将所有有理数都标到数轴上,那么数轴 填满吗?BA每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一点都表示一个实数。C数轴上的点有些
表示有理数,有
些表示无理数.11实数与数轴上的点是一一对应的。事实上,每一个无理数都可以用数轴上的一个点来表示出来。问题3.你能在平面直角坐标系中描出点( ,1)吗?( ,1)有序实数对xy ★平面直角坐标系中的点与有序实数对之间也是一 一对应的.巩固提高1、(1)请将数轴上是各点与下列实数对应起来:ABCDE 3(2)比较它们的大小(用“<”号连接)在数轴上表示的两个实数,右边的数总比左边的数大。3、在数轴上与原点的距离是 的点所表示的数是 。巩固提高4、在数轴上距离表示-2的点是 个
单位长度的数是 。2、设 对应数轴上的点是A, 对应数轴上的点是B,那么A、B间的距离是 。使我感触最深的是……
我学会了……
我感到困难的是……
我想我将…… 小结交流通过这节课的学习说说你的收获:你学会了吗?有理数无理数分数整数有限小数或
无限循环小数无限不循环小数实数
(按定义分)归纳总结★实数和数轴上的点是一一对应的. ★有序实数对和平面直角坐标系中的点是一 一对应的.作业课时作业:第2题课后练习: 第1题课本P86:习题13.3
课外学习:阅读与思考课本P88的材料挑战的相反数
的绝对值 在数学天地里,重要的不是我们知道什么,而是我们怎么知道—— 毕达哥拉斯结束寄语再见
