11.1 全等三角形
图片预览



文档简介
课件25张PPT。11.1全等三角形下列各组图形的形状与大小有什么特点?能够完全重合的两个图形叫做全等形(1)(2)(3)(4)形状和大小
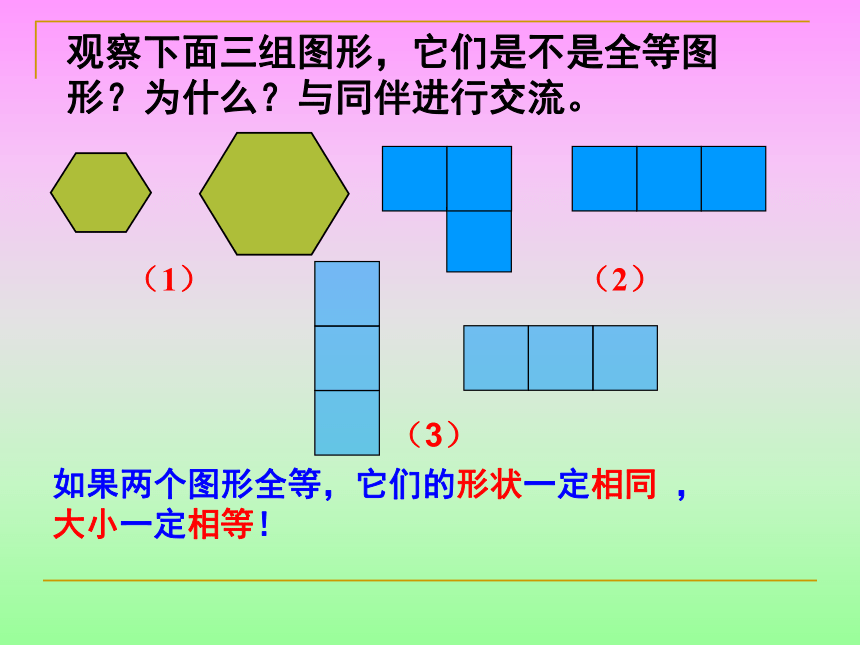
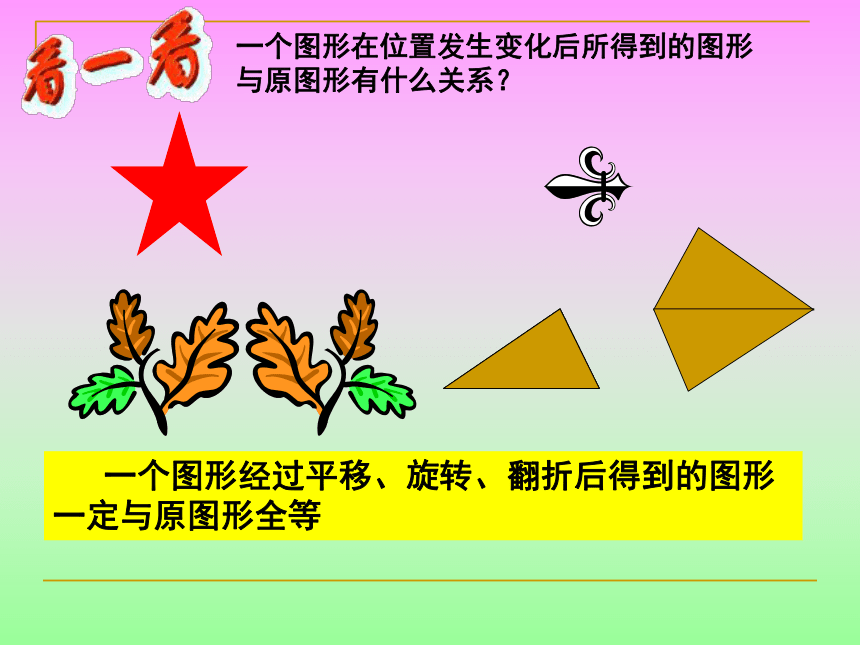
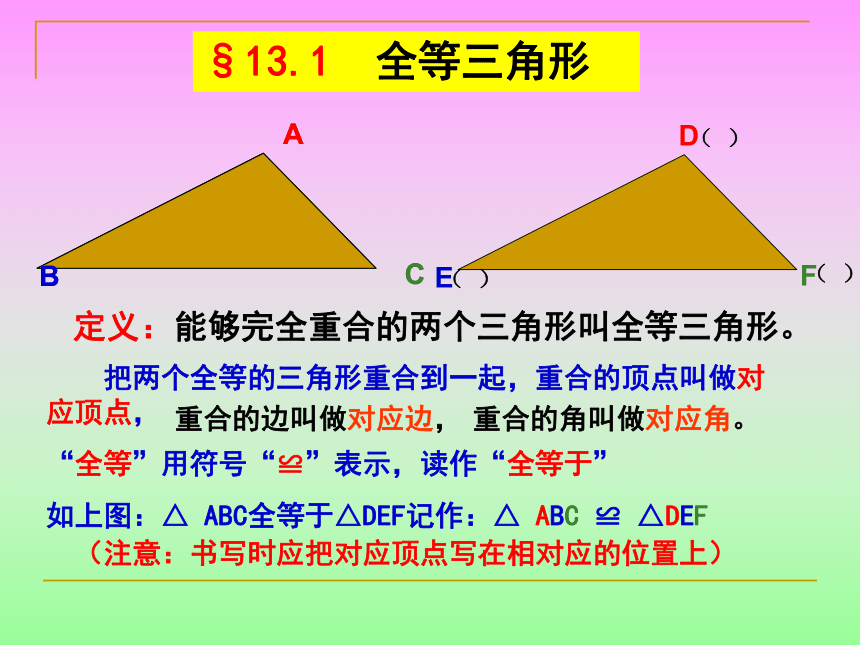
都相同观察下面三组图形,它们是不是全等图形?为什么?与同伴进行交流。(1)(2)如果两个图形全等,它们的形状一定相同 ,大小一定相等!(3)形状不同大小不同 一个图形经过平移、旋转、翻折后得到的图形一定与原图形全等一个图形在位置发生变化后所得到的图形与原图形有什么关系?§13.1 全等三角形DEF定义:能够完全重合的两个三角形叫全等三角形。 把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,
“全等”用符号“≌”表示,读作“全等于”
如上图:△ ABC全等于△DEF记作:△ ABC ≌ △DEF
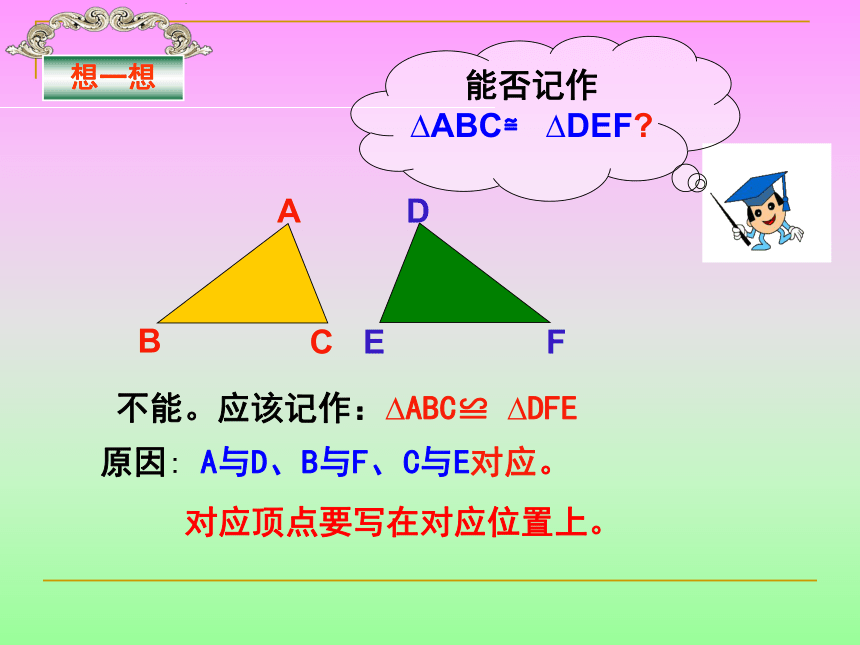
(注意:书写时应把对应顶点写在相对应的位置上)重合的边叫做对应边,重合的角叫做对应角。想一想能否记作?ABC≌ ?DEF?不能。应该记作:?ABC≌ ?DFE原因: A与D、B与F、C与E对应。
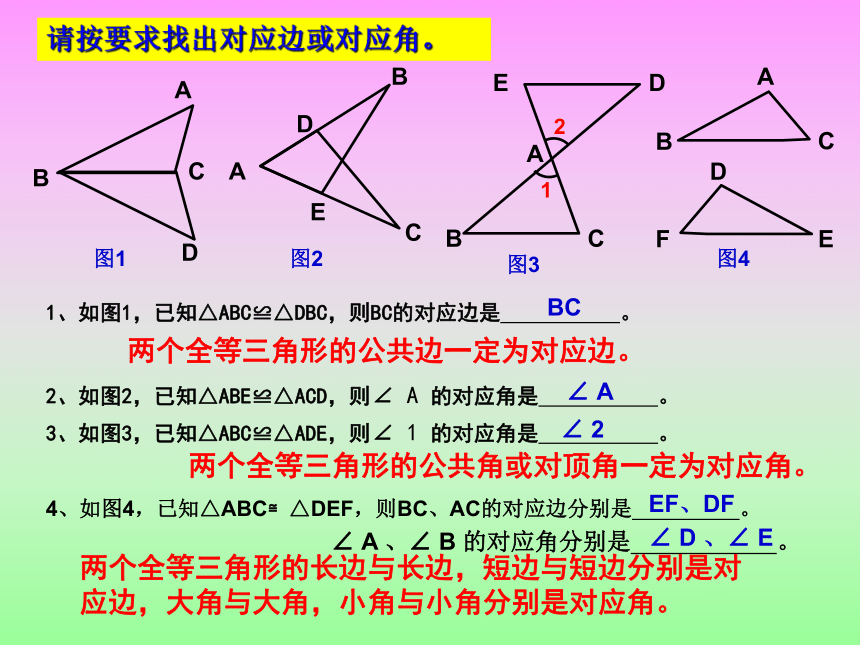
对应顶点要写在对应位置上。1、如图1,已知△ABC≌△DBC,则BC的对应边是 。请按要求找出对应边或对应角。2、如图2,已知△ABE≌△ACD,则∠ A 的对应角是 。两个全等三角形的公共边一定为对应边。3、如图3,已知△ABC≌△ADE,则∠ 1 的对应角是 。两个全等三角形的公共角或对顶角一定为对应角。4、如图4,已知△ABC≌△DEF,则BC、AC的对应边分别是 。
∠ A 、∠ B 的对应角分别是 。两个全等三角形的长边与长边,短边与短边分别是对应边,大角与大角,小角与小角分别是对应角。BCEF、DF∠ A∠ 2∠ D 、∠ E小试身手
问题一:下列说法是否正确: (1) 同一面中华人民共和国国旗上,4个小五 角星都是全等形。× √(4) 半径相等的两个圆是全等形。 √(2)全等三角形的周长相等,面积也相等。 (3) 周长相等的两个三角形是全等三角形。√ACBDEABCD图1图2图3图4图5ABDC 一个三角形经过平移、旋转、翻折后所得到的三角形与原三角形全等。ADE观察ABCDEF全等三角形的性质:全等三角形的对应边相等,对应角相等。如图:∵△ABC≌△DEF
∴AB=DE,BC=EF,AC=DF
( )
∴∠A=∠D,∠B=∠E,∠C=∠F
( )全等三角形的对应边相等全等三角形的对应角相等例题讲解,掌握新知例:如图, △ABC≌△DCB,
指出所有的对应边和对应角。O解:∵△ABC≌△DCB
∴AB与DC,BC与CB,AC与BD是对应边
∠A与∠ D,∠ABC与∠DCB,∠ACB与∠DBC是对应角变式:若上图中△ABO≌△DCO,试写出这两个三角形中
相等的边和相等的角。解:∵△ABO≌△DCO
∴AB=DC,BO=CO,AO=DO
∠A=∠ D,∠ABO=∠DCO,∠AOB=∠DOC 1.记两个三角形全等时,通常把表示对应顶点的字母写在 ;
填空题对应位置CD 2.两个三角形全等时,对应边所对的角是 ,
对应角所对的边是 。 对应角对应边如图, △ABD ≌ △EBC2、如果AB=3cm,BC=5cm, 求BE、BD的长. ∴BE=3cm,BD=5cm解:∵△ABD ≌ △EBC∴AB=EB,BC=BD∵AB=3cm,BC=5cm1、请找出对应边和对应角。 (全等三角形的对应边相等)AB EB、BC BD、AD EC,∠A ∠BEC、∠D ∠C、∠ABD ∠EBC=与与与与与与=====已知△ABD ≌ △EBC 且AB=3cm,DE=2cm,求BC的长.∴BE=3cm解:∵△ABD ≌ △EBC∴AB=BE,BC=BD ( ? )∵AB=3cm∴BC=BD=DE+BE =2+3=5cm如图,△ABD≌△ACE,若∠ADB=100O, ∠B=30O,你能说出△ACE中各角的大小吗?解:∵ △ABD≌△ACE,
∴∠AEC= ∠ADB=100O ,∠C= ∠B=30O,
又∵∠A+∠AEC+∠C=180°
∴∠A=180O- ∠AEC- ∠C
=180O-100O-30O=50O 看谁更聪明4312ACBD如图△ABC≌ △CDA,AB和CD、BC和DA是对应边,说出对应角和另外一组对应边,以下是李华同学的解答过程,你认为对吗?如果不对,正确的答案是什么?慧眼辨是非解:∵△ABC≌△CDA
∴∠1与∠ 2,∠3与∠4,∠B与∠D是对应角
AC与AC对应边 做错啦!!想想看:上题中边AB、CD位置上有什么关系?找一找:请指出下列全等三角形的对应边和对应角1、 △ ABE ≌ △ ACF对应角是: ∠A和∠A、 ∠ABE和∠ACF、 ∠AEB和∠AFC;对应边是AB和AC、AE和AF、BE和CF。2、 △ BCE ≌ △ CBF对应角是: ∠BCE和 ∠CBF、 ∠BEC和∠CFB、 ∠CBE和 ∠BCF。对应边是:CB和BC、CE和BF、CF和BE。3、 △ BOF ≌ △ COE对应角是: ∠BOF和∠COE、 ∠BFO 和∠CEO、 ∠ FOB和∠EOC。对应边是:OF和OE、OB和OC、BF和CE。 右图是一个等边三角形,你能把它分成两个全等的三角形吗?试一试 你能把它分成四个全等的三角形吗?你能把它分成三个全等的三角形吗? 你能把它分成六个全等的三角形吗?如图,已知△ AOC ≌ △BOD
说明:AC∥BD的理由能力提高思考题:把四边形ABCD纸片沿EF折叠使
点C落在四边形ABCD内部,如图,则
∠C与∠1+∠2之间的一种数量关系
始终保持不变,这个规律是( )∠C=∠1+∠2
2∠C=∠1+∠2
3∠C=∠1+∠2
3∠C=2(∠1+∠2)ABCD12EFC′B全等三角形1、本节课主要研究的内容:全等形的定义:能够完全重合的两个图形叫做全等形.定义:能够完全重合的两个三角形叫做全等三角形.表示方法:△ABC≌△DEF(对应点要写在对应
的位置上).性质:对应边相等,对应角相等.会用全等三角形的性质解决简单的问题.2、注意:两个全等三角形中,对应角所对的边是对
应边,对应边所对的角是对应角.例2.如图, △ABC≌△ADE,
∠C=50°,∠D=45°,
∠CFA=75°,求∠ BAC和∠BAE
的度数. ABCDEF再见学习几何的关键是要开动脑筋
都相同观察下面三组图形,它们是不是全等图形?为什么?与同伴进行交流。(1)(2)如果两个图形全等,它们的形状一定相同 ,大小一定相等!(3)形状不同大小不同 一个图形经过平移、旋转、翻折后得到的图形一定与原图形全等一个图形在位置发生变化后所得到的图形与原图形有什么关系?§13.1 全等三角形DEF定义:能够完全重合的两个三角形叫全等三角形。 把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,
“全等”用符号“≌”表示,读作“全等于”
如上图:△ ABC全等于△DEF记作:△ ABC ≌ △DEF
(注意:书写时应把对应顶点写在相对应的位置上)重合的边叫做对应边,重合的角叫做对应角。想一想能否记作?ABC≌ ?DEF?不能。应该记作:?ABC≌ ?DFE原因: A与D、B与F、C与E对应。
对应顶点要写在对应位置上。1、如图1,已知△ABC≌△DBC,则BC的对应边是 。请按要求找出对应边或对应角。2、如图2,已知△ABE≌△ACD,则∠ A 的对应角是 。两个全等三角形的公共边一定为对应边。3、如图3,已知△ABC≌△ADE,则∠ 1 的对应角是 。两个全等三角形的公共角或对顶角一定为对应角。4、如图4,已知△ABC≌△DEF,则BC、AC的对应边分别是 。
∠ A 、∠ B 的对应角分别是 。两个全等三角形的长边与长边,短边与短边分别是对应边,大角与大角,小角与小角分别是对应角。BCEF、DF∠ A∠ 2∠ D 、∠ E小试身手
问题一:下列说法是否正确: (1) 同一面中华人民共和国国旗上,4个小五 角星都是全等形。× √(4) 半径相等的两个圆是全等形。 √(2)全等三角形的周长相等,面积也相等。 (3) 周长相等的两个三角形是全等三角形。√ACBDEABCD图1图2图3图4图5ABDC 一个三角形经过平移、旋转、翻折后所得到的三角形与原三角形全等。ADE观察ABCDEF全等三角形的性质:全等三角形的对应边相等,对应角相等。如图:∵△ABC≌△DEF
∴AB=DE,BC=EF,AC=DF
( )
∴∠A=∠D,∠B=∠E,∠C=∠F
( )全等三角形的对应边相等全等三角形的对应角相等例题讲解,掌握新知例:如图, △ABC≌△DCB,
指出所有的对应边和对应角。O解:∵△ABC≌△DCB
∴AB与DC,BC与CB,AC与BD是对应边
∠A与∠ D,∠ABC与∠DCB,∠ACB与∠DBC是对应角变式:若上图中△ABO≌△DCO,试写出这两个三角形中
相等的边和相等的角。解:∵△ABO≌△DCO
∴AB=DC,BO=CO,AO=DO
∠A=∠ D,∠ABO=∠DCO,∠AOB=∠DOC 1.记两个三角形全等时,通常把表示对应顶点的字母写在 ;
填空题对应位置CD 2.两个三角形全等时,对应边所对的角是 ,
对应角所对的边是 。 对应角对应边如图, △ABD ≌ △EBC2、如果AB=3cm,BC=5cm, 求BE、BD的长. ∴BE=3cm,BD=5cm解:∵△ABD ≌ △EBC∴AB=EB,BC=BD∵AB=3cm,BC=5cm1、请找出对应边和对应角。 (全等三角形的对应边相等)AB EB、BC BD、AD EC,∠A ∠BEC、∠D ∠C、∠ABD ∠EBC=与与与与与与=====已知△ABD ≌ △EBC 且AB=3cm,DE=2cm,求BC的长.∴BE=3cm解:∵△ABD ≌ △EBC∴AB=BE,BC=BD ( ? )∵AB=3cm∴BC=BD=DE+BE =2+3=5cm如图,△ABD≌△ACE,若∠ADB=100O, ∠B=30O,你能说出△ACE中各角的大小吗?解:∵ △ABD≌△ACE,
∴∠AEC= ∠ADB=100O ,∠C= ∠B=30O,
又∵∠A+∠AEC+∠C=180°
∴∠A=180O- ∠AEC- ∠C
=180O-100O-30O=50O 看谁更聪明4312ACBD如图△ABC≌ △CDA,AB和CD、BC和DA是对应边,说出对应角和另外一组对应边,以下是李华同学的解答过程,你认为对吗?如果不对,正确的答案是什么?慧眼辨是非解:∵△ABC≌△CDA
∴∠1与∠ 2,∠3与∠4,∠B与∠D是对应角
AC与AC对应边 做错啦!!想想看:上题中边AB、CD位置上有什么关系?找一找:请指出下列全等三角形的对应边和对应角1、 △ ABE ≌ △ ACF对应角是: ∠A和∠A、 ∠ABE和∠ACF、 ∠AEB和∠AFC;对应边是AB和AC、AE和AF、BE和CF。2、 △ BCE ≌ △ CBF对应角是: ∠BCE和 ∠CBF、 ∠BEC和∠CFB、 ∠CBE和 ∠BCF。对应边是:CB和BC、CE和BF、CF和BE。3、 △ BOF ≌ △ COE对应角是: ∠BOF和∠COE、 ∠BFO 和∠CEO、 ∠ FOB和∠EOC。对应边是:OF和OE、OB和OC、BF和CE。 右图是一个等边三角形,你能把它分成两个全等的三角形吗?试一试 你能把它分成四个全等的三角形吗?你能把它分成三个全等的三角形吗? 你能把它分成六个全等的三角形吗?如图,已知△ AOC ≌ △BOD
说明:AC∥BD的理由能力提高思考题:把四边形ABCD纸片沿EF折叠使
点C落在四边形ABCD内部,如图,则
∠C与∠1+∠2之间的一种数量关系
始终保持不变,这个规律是( )∠C=∠1+∠2
2∠C=∠1+∠2
3∠C=∠1+∠2
3∠C=2(∠1+∠2)ABCD12EFC′B全等三角形1、本节课主要研究的内容:全等形的定义:能够完全重合的两个图形叫做全等形.定义:能够完全重合的两个三角形叫做全等三角形.表示方法:△ABC≌△DEF(对应点要写在对应
的位置上).性质:对应边相等,对应角相等.会用全等三角形的性质解决简单的问题.2、注意:两个全等三角形中,对应角所对的边是对
应边,对应边所对的角是对应角.例2.如图, △ABC≌△ADE,
∠C=50°,∠D=45°,
∠CFA=75°,求∠ BAC和∠BAE
的度数. ABCDEF再见学习几何的关键是要开动脑筋
