11.2 三角形全等的条件1
文档属性
| 名称 | 11.2 三角形全等的条件1 |

|
|
| 格式 | rar | ||
| 文件大小 | 65.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-11-07 00:00:00 | ||
图片预览


文档简介
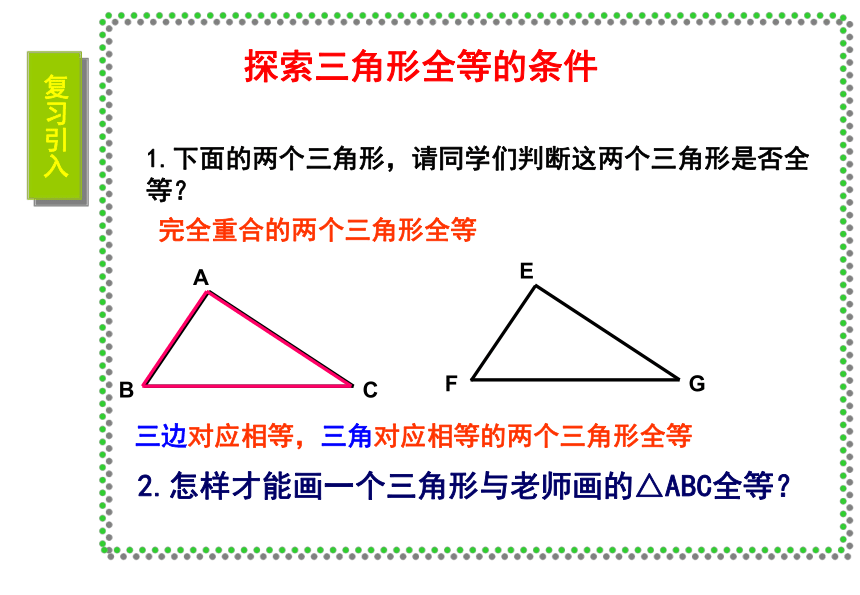
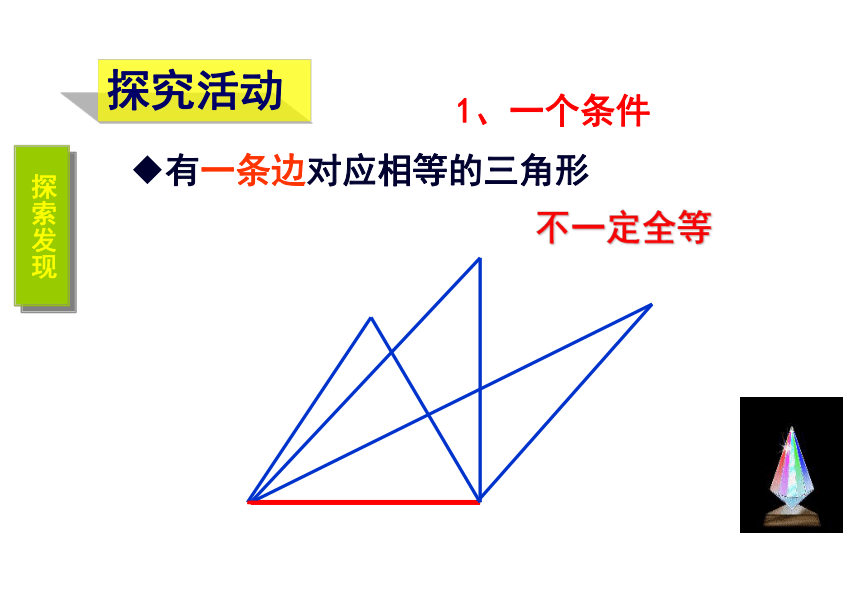
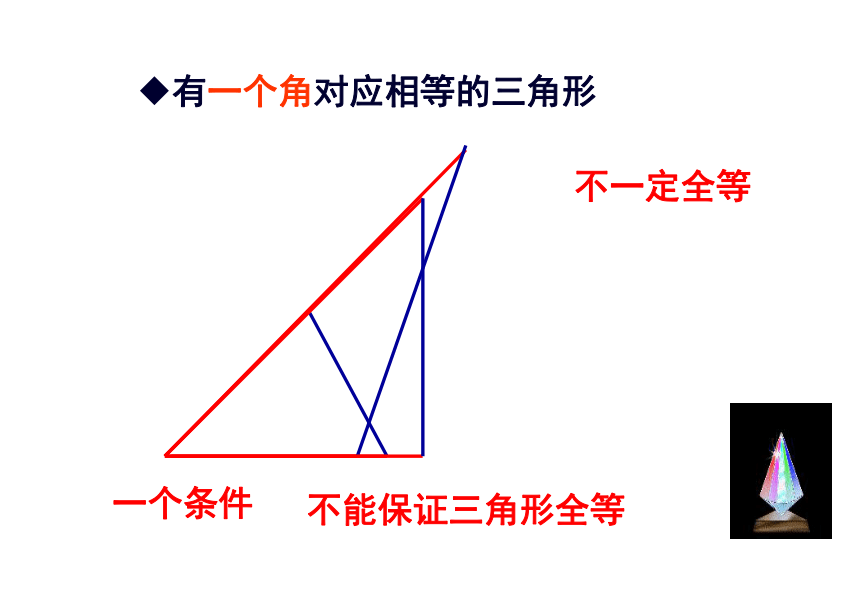
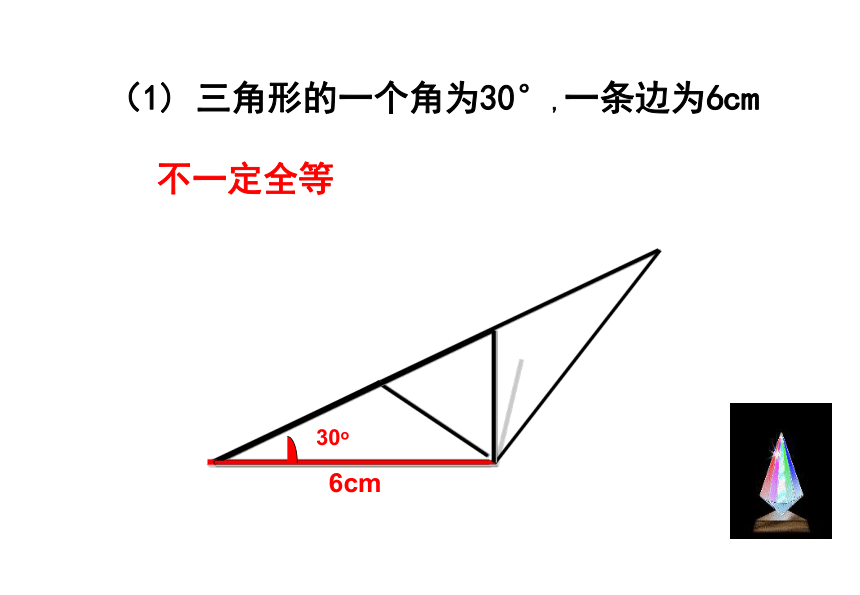
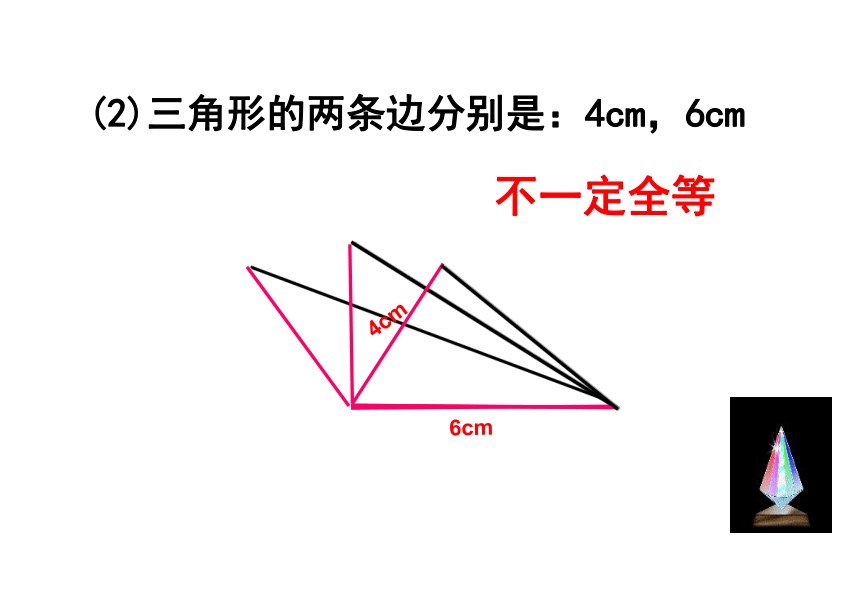
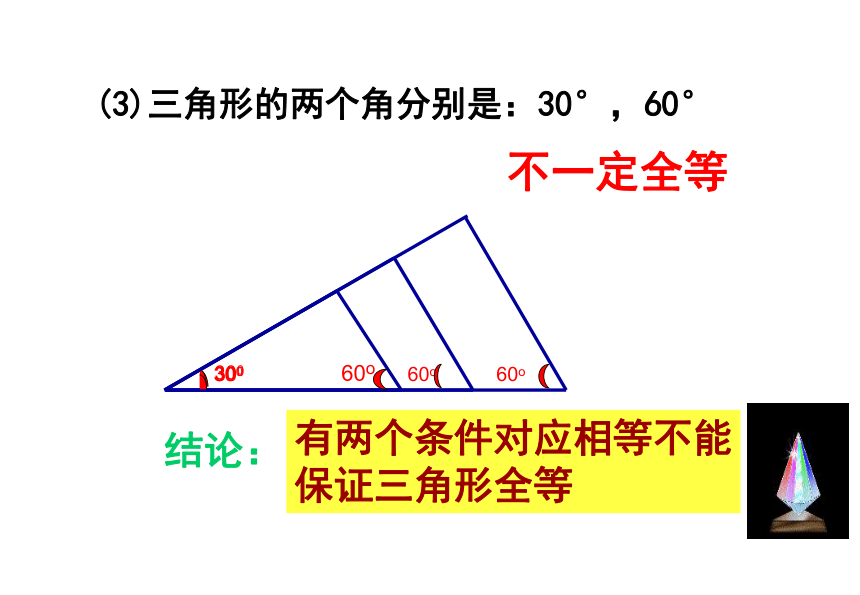
课件23张PPT。11.2 三角形全等的条件(1)复习引入1.下面的两个三角形,请同学们判断这两个三角形是否全 等?2.怎样才能画一个三角形与老师画的△ABC全等?探索三角形全等的条件 三边对应相等,三角对应相等的两个三角形全等完全重合的两个三角形全等 1、一个条件有一条边对应相等的三角形不一定全等探究活动探索发现有一个角对应相等的三角形不一定全等 一个条件不能保证三角形全等2、按照下面给出的两个条件画出三角形,并将完成的三角形比一比(1)三角形的一个角为 30°,一条边为6cm ;探究活动(2)三角形的两条边分别是 4cm 和 6cm ;(3)三角形的两个角分别是 30°和 60°.(1) 三角形的一个角为30°,一条边为6cm不一定全等(2)三角形的两条边分别是:4cm,6cm不一定全等(3)三角形的两个角分别是:30°,60°不一定全等结论:有两个条件对应相等不能
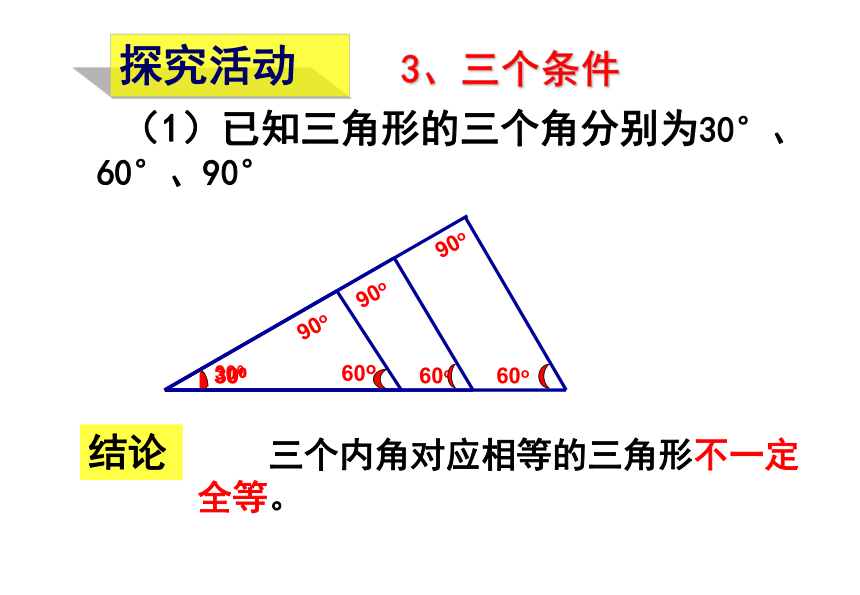
保证三角形全等 (1)已知三角形的三个角分别为30°、60°、90° 三个内角对应相等的三角形不一定 全等。探究活动3、三个条件结论按照三角形“边、角” 元素进行分类复习引入 先任意画出一个△ABC,再画一个△DEF,使DE=AB, EF=BC , DF=AC, 画好的△DEF与△ABC 全等吗?探究一D1、画线段EF=BC2、分别以E、F为圆心,线段BA、CA为半径画弧,两弧交于点D3、连接线段DE,DF
△DEF就是所求的三角形边边边公理 有三边对应相等的两个三角形全等.
可以简写成 “边边边” 或“ SSS ” S —— 边AB=EFAC=EG(SSS)规范书写:BC=FG在△ABC和△EFG中例1:已知: 如图,AC=AD ,BC=BD. 求证: △ACB ≌ △ADB.
ABCD说明:
△ACB ≌ △ADB.
这两个条件够吗?
还要什么条件呢?例题2 如图, △ABC 是一个钢架,AB = AC ,AD是
连结点A与BC中点D的支架.
求证: △ABD ≌ △ACD ACDB证明:在△ABD 和△ACD中AB = AC ∴ △ABD ≌ △ACD(已知)(公共边)(已证)AD = ADDB = DC( SSS )∵D是BC的中点 ,∴BD=CD动 态 演 示思考:图1已知:如图1 ,AC=FE,AD=FB,BC=DE
求证:△ABC≌△FDE 证明:∵ AD=FB
∴AD+DB=FB+BD(等式性质)
即AB=FD
在△ABC和△FDE 中AC=FE(已知)
BC=DE(已知)
AB=FD(已证)
∴△ABC≌△FDE(SSS)若求证∠C=∠E ,如何证明?思考:问:
动 态 演 示变式1练习:1.已知:如图2,点A、B、C、D在同一条直线上,AC=DB,AE=DF,BE=CF图2求证:(1)△EAB≌△FDC、(2)DF= AE应用拓展应用拓展聪明题 你会吗已知如图四边形ABCD是平行四边形,
求证: ∠A= ∠C。A C D B分析:要证两个角等或两条线段等,常需要先证这两角或两线段
所在的两个三角形全等。而构造两个全等三角形,连接公共边
是最常见的辅助线。想一想:还有其他的方法吗?这就是转化思想?练一练:
已知如图,AB=AC,DB=DC,说明∠B =∠C成立的理由ABCD在△ABD和△ACD中,AB=AC (已知)DB=DC (已知) AD=AD (公共边)∴△ABD≌△ACD (SSS)解:连接AD∴ ∠B =∠C(全等三角形的对应角相等)你会用转化思想吗?1.边边边公理:有三边对应相等的两个三角形全等 简写成“边边边”(SSS)2.边边边公理的发现过程所用到的数学方法(包括画 图、猜想、分析、归纳等.)3.边边边公理的应用中所用到的数学方法:
证明线段(或角相等)转 化 证明线段(或角)所在的两个三角形全等.用结论说明两个三角形全等需注意1. 说明两个三角形全等所需的条件应按对应边的顺序书写.
2. 结论中所出现的边必须在所证明的两个三角形中. 归纳:
保证三角形全等 (1)已知三角形的三个角分别为30°、60°、90° 三个内角对应相等的三角形不一定 全等。探究活动3、三个条件结论按照三角形“边、角” 元素进行分类复习引入 先任意画出一个△ABC,再画一个△DEF,使DE=AB, EF=BC , DF=AC, 画好的△DEF与△ABC 全等吗?探究一D1、画线段EF=BC2、分别以E、F为圆心,线段BA、CA为半径画弧,两弧交于点D3、连接线段DE,DF
△DEF就是所求的三角形边边边公理 有三边对应相等的两个三角形全等.
可以简写成 “边边边” 或“ SSS ” S —— 边AB=EFAC=EG(SSS)规范书写:BC=FG在△ABC和△EFG中例1:已知: 如图,AC=AD ,BC=BD. 求证: △ACB ≌ △ADB.
ABCD说明:
△ACB ≌ △ADB.
这两个条件够吗?
还要什么条件呢?例题2 如图, △ABC 是一个钢架,AB = AC ,AD是
连结点A与BC中点D的支架.
求证: △ABD ≌ △ACD ACDB证明:在△ABD 和△ACD中AB = AC ∴ △ABD ≌ △ACD(已知)(公共边)(已证)AD = ADDB = DC( SSS )∵D是BC的中点 ,∴BD=CD动 态 演 示思考:图1已知:如图1 ,AC=FE,AD=FB,BC=DE
求证:△ABC≌△FDE 证明:∵ AD=FB
∴AD+DB=FB+BD(等式性质)
即AB=FD
在△ABC和△FDE 中AC=FE(已知)
BC=DE(已知)
AB=FD(已证)
∴△ABC≌△FDE(SSS)若求证∠C=∠E ,如何证明?思考:问:
动 态 演 示变式1练习:1.已知:如图2,点A、B、C、D在同一条直线上,AC=DB,AE=DF,BE=CF图2求证:(1)△EAB≌△FDC、(2)DF= AE应用拓展应用拓展聪明题 你会吗已知如图四边形ABCD是平行四边形,
求证: ∠A= ∠C。A C D B分析:要证两个角等或两条线段等,常需要先证这两角或两线段
所在的两个三角形全等。而构造两个全等三角形,连接公共边
是最常见的辅助线。想一想:还有其他的方法吗?这就是转化思想?练一练:
已知如图,AB=AC,DB=DC,说明∠B =∠C成立的理由ABCD在△ABD和△ACD中,AB=AC (已知)DB=DC (已知) AD=AD (公共边)∴△ABD≌△ACD (SSS)解:连接AD∴ ∠B =∠C(全等三角形的对应角相等)你会用转化思想吗?1.边边边公理:有三边对应相等的两个三角形全等 简写成“边边边”(SSS)2.边边边公理的发现过程所用到的数学方法(包括画 图、猜想、分析、归纳等.)3.边边边公理的应用中所用到的数学方法:
证明线段(或角相等)转 化 证明线段(或角)所在的两个三角形全等.用结论说明两个三角形全等需注意1. 说明两个三角形全等所需的条件应按对应边的顺序书写.
2. 结论中所出现的边必须在所证明的两个三角形中. 归纳:
