11.2.三角形全等的条件(四)
文档属性
| 名称 | 11.2.三角形全等的条件(四) |  | |
| 格式 | rar | ||
| 文件大小 | 374.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-11-07 14:54:00 | ||
图片预览

文档简介
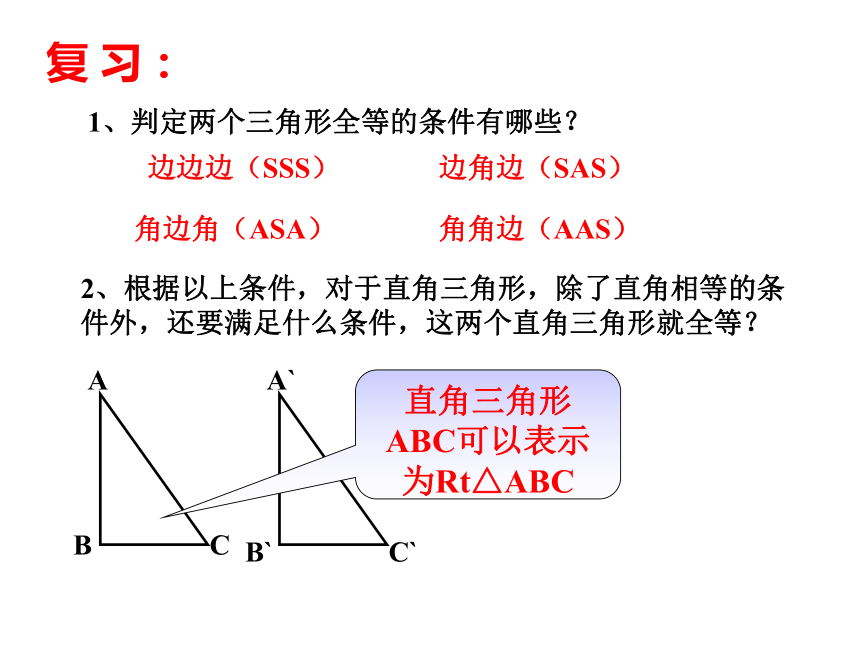
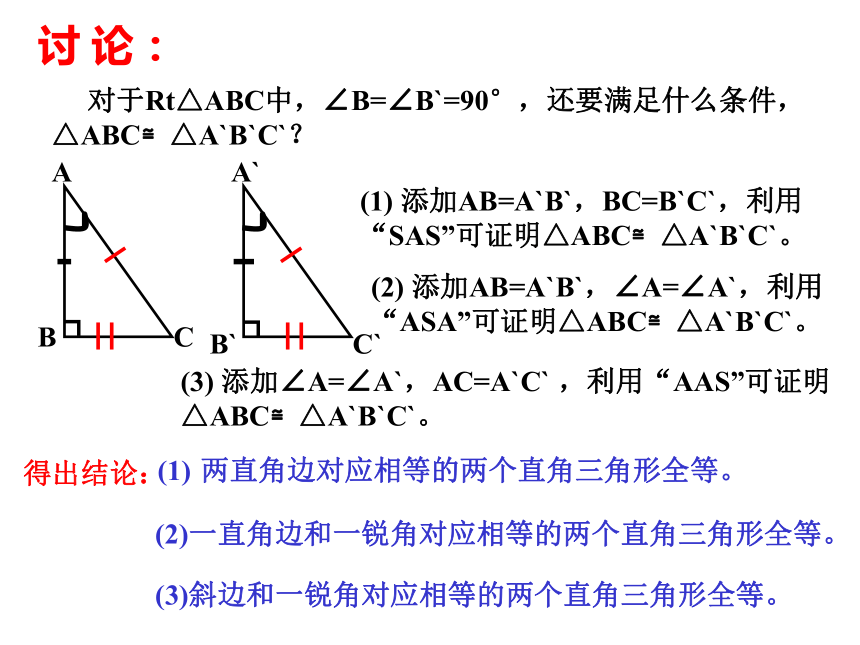
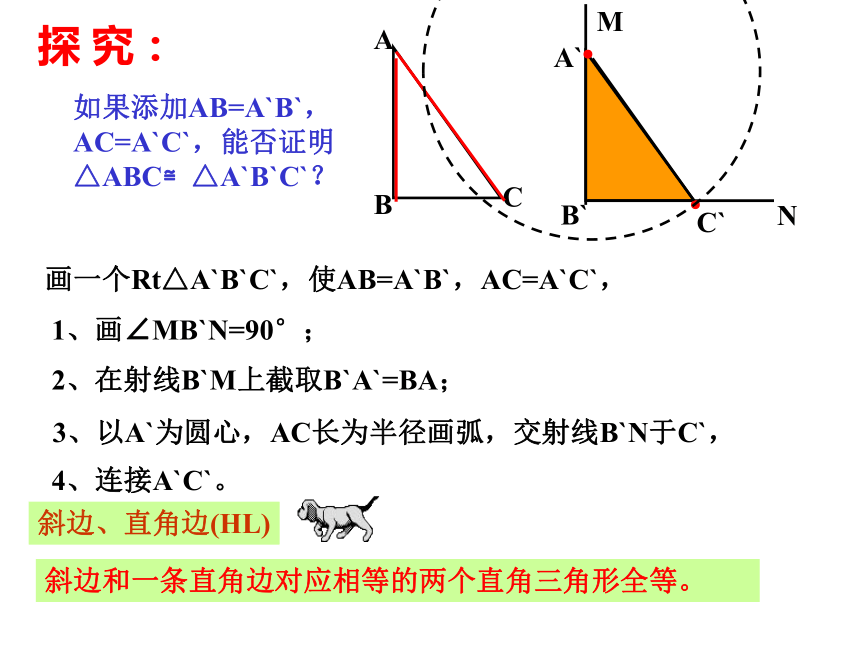
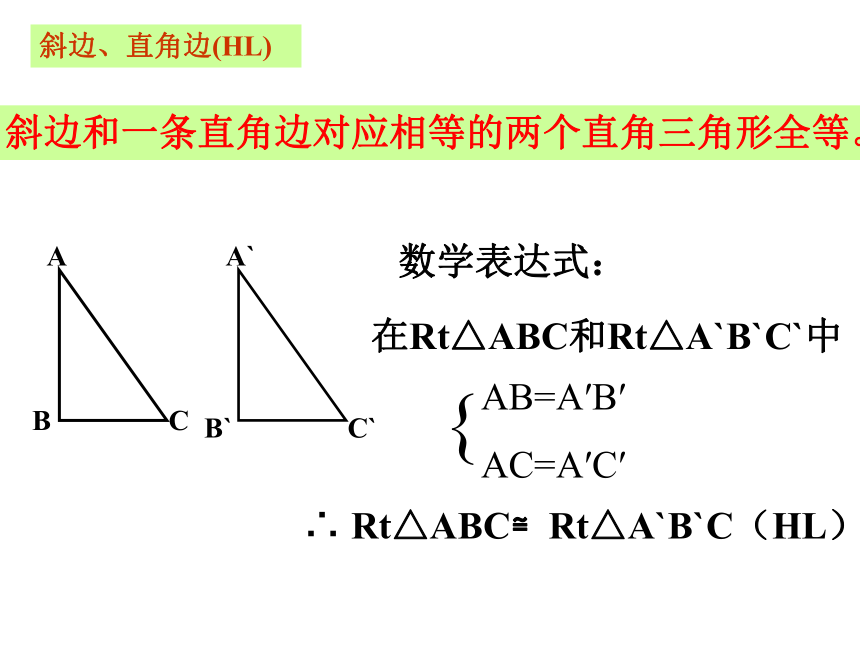
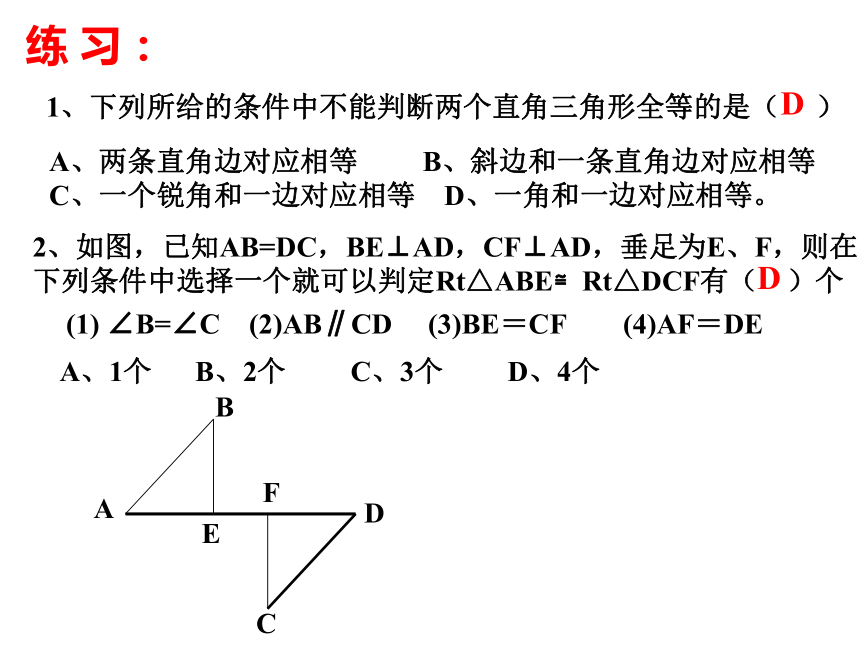
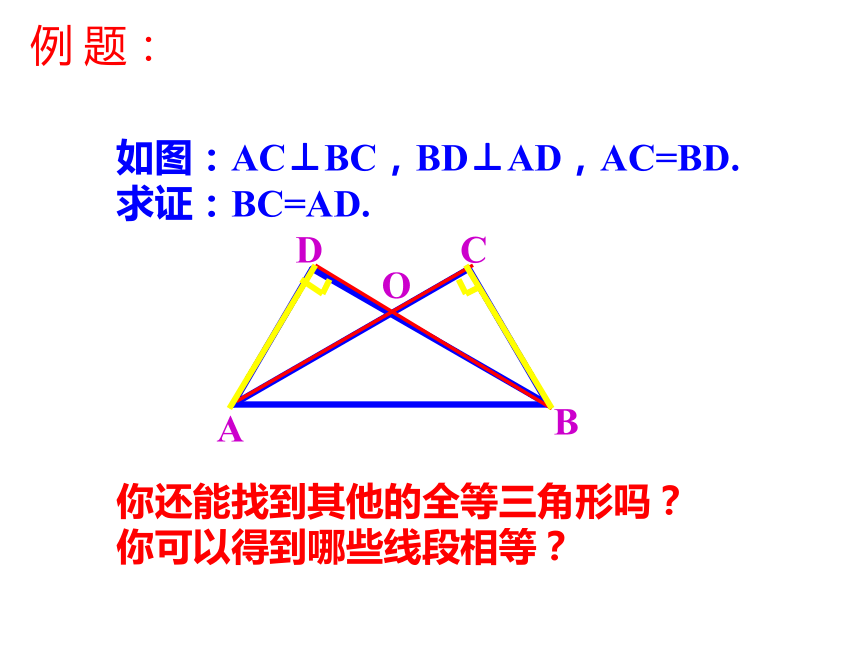
课件14张PPT。三角形全等的条件(四)复 习:1、判定两个三角形全等的条件有哪些?边角边(SAS)2、根据以上条件,对于直角三角形,除了直角相等的条件外,还要满足什么条件,这两个直角三角形就全等?直角三角形ABC可以表示为Rt△ABC边边边(SSS)角角边(AAS)角边角(ASA)讨 论: 对于Rt△ABC中,∠B=∠B`=90°,还要满足什么条件,△ABC≌△A`B`C`?(1) 添加AB=A`B`,BC=B`C`,利用“SAS”可证明△ABC≌△A`B`C`。(2) 添加AB=A`B`,∠A=∠A`,利用“ASA”可证明△ABC≌△A`B`C`。(3) 添加∠A=∠A`,AC=A`C` ,利用“AAS”可证明△ABC≌△A`B`C`。得出结论:两直角边对应相等的两个直角三角形全等。(2)一直角边和一锐角对应相等的两个直角三角形全等。(3)斜边和一锐角对应相等的两个直角三角形全等。┓┓如果添加AB=A`B`,AC=A`C`,能否证明 △ABC≌△A`B`C`?A`B`C`探 究:MN●●画一个Rt△A`B`C`,使AB=A`B`,AC=A`C`,1、画∠MB`N=90°;2、在射线B`M上截取B`A`=BA;3、以A`为圆心,AC长为半径画弧,交射线B`N于C`,4、连接A`C`。斜边、直角边(HL)斜边和一条直角边对应相等的两个直角三角形全等。斜边和一条直角边对应相等的两个直角三角形全等。斜边、直角边(HL)在Rt△ABC和Rt△A`B`C`中∴ Rt△ABC≌Rt△A`B`C(HL)数学表达式:练 习:1、下列所给的条件中不能判断两个直角三角形全等的是( )A、两条直角边对应相等 B、斜边和一条直角边对应相等 C、一个锐角和一边对应相等 D、一角和一边对应相等。2、如图,已知AB=DC,BE⊥AD,CF⊥AD,垂足为E、F,则在下列条件中选择一个就可以判定Rt△ABE≌Rt△DCF有( )个(1) ∠B=∠C (2)AB∥CD (3)BE=CF (4)AF=DEA、1个 B、2个 C、3个 D、4个DD如图:AC⊥BC,BD⊥AD,AC=BD.求证:BC=AD.你还能找到其他的全等三角形吗?
你可以得到哪些线段相等?例 题: 如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE大小有什么关系? 如图,E,F分别为线段AC上的两个点,且DE⊥AC于E点,BF⊥AC于F点,若AB=CD,AF=CE,BD交AC于M点.求证:MB=MD,ME=MF; 如图,E,F分别为线段AC上的两个动点,且DE⊥AC于E点,BF⊥AC于F点,若AB=CD,AF=CE,BD交AC于M点. 当E、F两点移动至如图的位置时,其余条件不变,上述结论能否成立?若成立,请给予证明.D 1.如图,C是路段AB的中点,两人 从C同时出发,以相同的速度分别 沿两条直线行走,并同时到达D,E两地,DA⊥AB,EB⊥AB,D,E与路段AB的距离相等吗?为什么?2.如图,AB=CD,AE⊥BC,
DF⊥BC,CE=BF.
求证:AE=DF.3、如图,AD、A`D`分别是△ABC和△A`B`C`中BC、B`C`边上的高,且AB=A`B`,AD=A`D`,若使△ABC≌△A`B`C`,请补充条件(只需填写一个你认为适当的条件)______________________。学习了本节课,你有什么收获?
你可以得到哪些线段相等?例 题: 如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE大小有什么关系? 如图,E,F分别为线段AC上的两个点,且DE⊥AC于E点,BF⊥AC于F点,若AB=CD,AF=CE,BD交AC于M点.求证:MB=MD,ME=MF; 如图,E,F分别为线段AC上的两个动点,且DE⊥AC于E点,BF⊥AC于F点,若AB=CD,AF=CE,BD交AC于M点. 当E、F两点移动至如图的位置时,其余条件不变,上述结论能否成立?若成立,请给予证明.D 1.如图,C是路段AB的中点,两人 从C同时出发,以相同的速度分别 沿两条直线行走,并同时到达D,E两地,DA⊥AB,EB⊥AB,D,E与路段AB的距离相等吗?为什么?2.如图,AB=CD,AE⊥BC,
DF⊥BC,CE=BF.
求证:AE=DF.3、如图,AD、A`D`分别是△ABC和△A`B`C`中BC、B`C`边上的高,且AB=A`B`,AD=A`D`,若使△ABC≌△A`B`C`,请补充条件(只需填写一个你认为适当的条件)______________________。学习了本节课,你有什么收获?
