第11章 图形与坐标学案

11.1 怎样确定平面内点的位置
一、学习目标：
1、通过生活中确定物体位置的丰富实例和不同办法，使学生经历确定物体位置的数学化的过程，感受生活与数学的联系。
2、在现实情境中感受确定物体位置的不同办法，会用一对有序数对确定物体的位置。
二、重点：确定平面内点的位置
难点：理解一对有序数对
三、学习过程：
(一)课前预习：确定点的位置有 和 两种方法；每种方法各包含两个要素,第一种是： 第二种是 。
（二）合作探究
自主学习：认真阅读课本46-47页内容，仔细考虑上面提出的每个问题，在你的小组内交流。
合作交流：小组合作交流，解决下列问题。
1.同学们在电影院寻找座位的过程中，确定自己的座位需几个数据？哪两个数据？
2.如果将你的座位3排2号简记为（3, 2），那么2排3号如何表示？（5, 6）表示什么含义？（2，7）的位置在哪里？你能用这种方法表示出自己的座位吗？
3.“3排2号”与“2排3号”中的“3”的含义相同吗？有什么不同？这说明了什么？
典型例题：
2008年5月12日，在四川汶川发生8.0级特大地震，能够准确表示汶川这个地点位置的是（ ）
A.北纬31° B.东经103.5° C.金华的西北方向上D.北纬31°，东经103.5°
（三）巩固练习
1.将图中所示的围棋棋盘放在某个平面直角坐标系内，
白棋②的坐标为（-7，-4），白棋④的坐标为（-6，-8），
那么黑棋的坐标应该是_________.
2.如图，表示经三路与纬一路的十字路口，表示经一路与三路的十字路口，如果用（3，1）→（3，2）→（3，3）→（2，3）→（1，3）表示由到的一条路径，用同样的方式写出另外一条由到的路径：
（3，1）→（ ）→（ ）→（ ）→（1，3）.
（四）小结与反思：本节课你学习了哪些知识？你掌握了吗？
（五）达标测试：
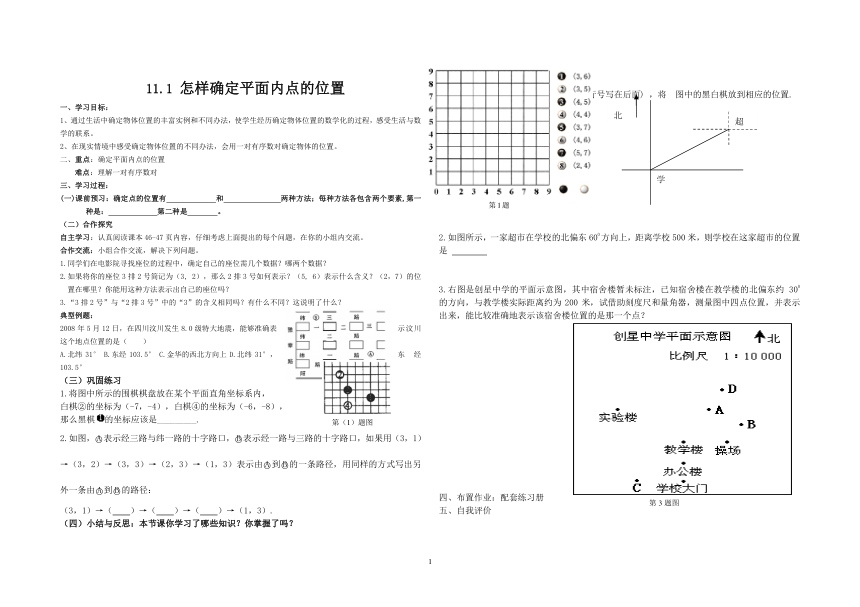
1.按照提供的有序数对(列号写在前面,行号写在后面) ，将 图中的黑白棋放到相应的位置.
2.如图所示，一家超市在学校的北偏东600方向上，距离学校500米，则学校在这家超市的位置是
3.右图是创星中学的平面示意图，其中宿舍楼暂未标注，已知宿舍楼在教学楼的北偏东约300的方向，与教学楼实际距离约为200米，试借助刻度尺和量角器，测量图中四点位置，并表示出来，能比较准确地表示该宿舍楼位置的是那一个点？
四、布置作业：配套练习册
五、自我评价
11.2平面直角坐标系
教师寄语：勤奋可以弥补聪明的不足，但聪明无法弥补懒惰的不足。
学习目标：
（一）【知识目标】
1、认识平面直角坐标系及其相关概念；
2、探索象限内点的特征与坐标轴上点的特征。
（二）【技能目标】
1、会正确画出平面直角坐标系；
2、在给定的平面直角坐标系中，能够根据坐标指出点的位置，并且已知点的位置写出它对应的坐标；
3、在给定的条件下，能够根据象限内点的特征与坐标轴上点的特征，结合特殊点，利用方程、不等式等已有的知识解决一些简单的数学问题；
（三）【情感目标】
1、培养学生严谨朴实的科学态度和勤奋自强的探索精神，以及独立思考与合作交流的学习习惯，感受数学之实。
2、让学生得到尝试、成功的情感体验，感受数学之美。
学习重点与难点：
1、教学重点：能在给定的平面直角坐标系中，由点求出坐标，由坐标描出点。
2、教学难点：探索象限内点的特征与坐标轴上点的特征，以及它们特征的简单运用。
学习过程：
一、拓通准备与预习
1、请指出数轴A点的坐标是
2、请在数轴上描出坐标是-3的点。
3、平面直角坐标系是指 ；
点的坐标由 与 组成。
二、创设情境、问题导学
我们的教室共有56个座位，自前向后分为7排，自左向右分为8列，每位学生对应了一个座位，我们来玩个“点将”游戏，你们是“将”，由我来点，点到的同学说出自己的座位号几排几列）。同时演示“点将”游戏，游戏规则：（1）老师报到学生姓名，学生起立并说出座位号；（2）老师说出座位号，对应的学生起立。奖励：同学们的掌声。
游戏后归纳：（1）归纳：要确定一个学生的座位必须有哪两个两个数决定？
（2）2排3列与3排2列是否是同一个座位？由此你认为表示座位与两个数的顺序有关吗？
三、合作探究
探究知识点1：平面直角坐标系
在纸上画出两条互相垂直而且有公共原点的数轴，
阅读教材49页内容，知道平面直角坐标系及相关概念。
探究知识点2：点的坐标概念
1、找A点的坐标方法：
在横轴和纵轴上有那么多的数，A点跟横轴上的哪个数有关系？A点跟纵轴上的哪个数有关系？由该点向X轴作垂线，找到第一个数是 ，所以我们就说A点的横坐标是 ，继续向Y轴作垂线找到第二个数是 ，所以我们就说A点的纵坐标是 ，现在我们已经找到了两个数，要是把这两个数排一下顺序，把谁放在前面？
A点的横坐标是
A点的纵坐标是
A点的坐标是：A（ ）
2、老师操作，学生说坐标：如上图B点
B点的横坐标是
B点的纵坐标是
B点的坐标是：B（ ）
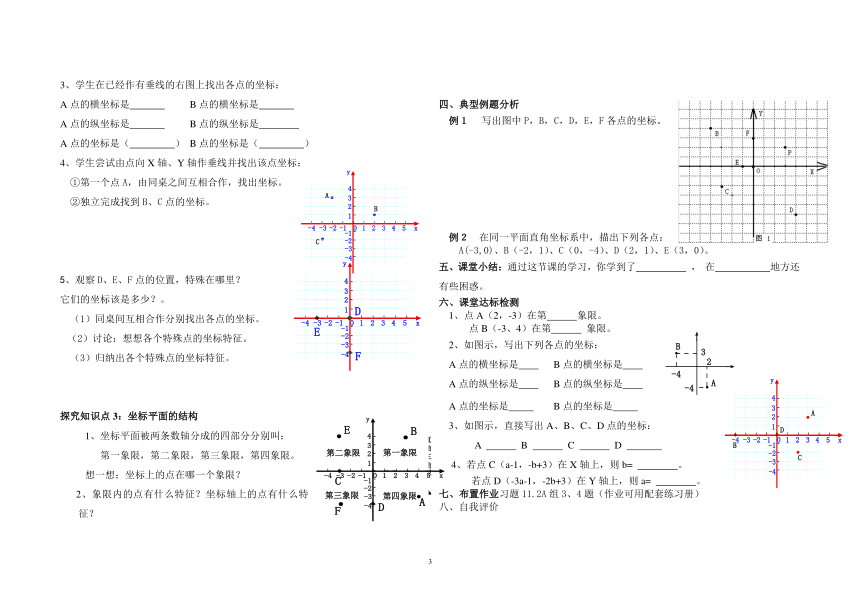
3、学生在已经作有垂线的右图上找出各点的坐标：
A点的横坐标是 B点的横坐标是
A点的纵坐标是 B点的纵坐标是
A点的坐标是（ ） B点的坐标是（ ）
4、学生尝试由点向X轴、Y轴作垂线并找出该点坐标：
①第一个点A，由同桌之间互相合作，找出坐标。
②独立完成找到B、C点的坐标。
5、观察D、E、F点的位置，特殊在哪里？
它们的坐标该是多少？。
（1）同桌间互相合作分别找出各点的坐标。
（2）讨论：想想各个特殊点的坐标特征。
（3）归纳出各个特殊点的坐标特征。
探究知识点3：坐标平面的结构
1、坐标平面被两条数轴分成的四部分分别叫：
第一象限，第二象限，第三象限，第四象限。
想一想：坐标上的点在哪一个象限？
2、象限内的点有什么特征？坐标轴上的点有什么特征？
四、典型例题分析
例1 写出图中P，B，C，D，E，F各点的坐标。
例２　在同一平面直角坐标系中，描出下列各点：
A(-3,0)、B（-2，1）、C（0，-4）、D（2，1）、E（3，0）。
五、课堂小结：通过这节课的学习，你学到了 ， 在 地方还有些困惑。
六、课堂达标检测
1、点A（2，-3）在第 象限。
点B（-3、4）在第 象限。
2、如图示，写出下列各点的坐标：
A点的横坐标是 B点的横坐标是
A点的纵坐标是 B点的纵坐标是
A点的坐标是 B点的坐标是
3、如图示，直接写出A、B、C、D点的坐标：
A B C D
4、若点C（a-1，-b+3）在X轴上，则b= 。
若点D（-3a-1，-2b+3）在Y轴上，则a= 。
七、布置作业习题11.2A组3、4题（作业可用配套练习册）
八、自我评价
11.3直角坐标系中的图形
教师寄语：学以致用是有效的学习方法之一。
学习目标：
1、在同一直角坐标系中，感受图形上点的坐标变化与图形的变化（平移，轴对称，伸长，压缩）之间的关系。
2、经历图形坐标变化与图形的平移，轴对称，伸长，压缩之间的关系的探索过程，发展学生的形象思维能力和数形结合意识。?
学习过程??
一，自主学习、导入新课：
在前几节课中我们学面直角坐标系的有关知识，会根据坐标描出点的位置，由点的位置写出它的坐标。下面拿出方格纸，并在方格纸上建立直角坐标系，找到下列各点，并依次用线段将这些点连接起来。坐标是（0，0），（5，4），（3，0），（5，1），（5，－1），（3，0），（4，－2），（0，0）。
观察所得的图形，你们决定它像什么？ 我们知道点的坐标决定点的位置，如果坐标按一定规律变化，那么图形是否会变化，变化的规律是怎样的，这将是本节课中我们要研究的问题。
二，合作探究：
1、组内交流：
将上图中的点（0，0），（5，4），（3，0），（5，1），（5，－1），（3，0）， （4，－2），（0，0）做以下变化：
（1）纵坐标保持不变，横坐标分别变成原来的2倍，再将所得的点用线段依次连接起来，所得的图案与原来的图案相比有什么变化？
（2）纵坐标保持不变，横坐标分别加3，再将所得的点用线段依次连接起来，所得的图案与原来的图案相比有什么变化？ 先根据题意把变化前后的坐标作一对比。 根据变化后的坐标，把变化后的图形在自己准备的方格纸上画出来。
这个图形与原来的图形相比有什么变化呢？
（a）所得图案与原图案相比，整条鱼横向拉长为原来的的2倍。即鱼变长了。 （b）新的图案与原图案相比，鱼的形状、大小不变，整条鱼向右平移了3个长度单位。
2、小结：从上面的两种变化情况来看，当横坐标分别加3，纵坐标不变时，整个图案向右平移了3个单位；当横坐标分别变成原来的2倍，纵坐标不变时，整条鱼被横向拉长为原来的2倍。
? 3、 议一议：如果纵坐标保持不变，横坐标分别变为原来的1/2，那么所得图案会发生什么变化？上述情况都是横坐标变化，纵坐标不变，图形被横向拉长、横向压缩或整体向右移动，总的都是在横向发生变化，那么当纵坐标发生变化，横坐标不变时，鱼会怎样变化呢？
4、将第一个图形中的点（0，0），（5，4），（3，0），（5，1），（5，－1），（3，0），（4，－2），（0，0）做如下变化：
（1）横坐标保持不变，纵坐标分别乘－1，所得的图案与原来的图案相比有什么变化？图形和原来图形相比，好像鱼沿x轴翻了个身。是的，所得的图案与 原图案关于横轴成轴对称。
（2）横、纵坐标分别变成原来的2倍，所得的图案与原来的图案相比有什么变化？所得的图案与原图案相比，形状不变、大小放大了一倍。
（3）你还能想出哪些变化？比如横坐标乘以－1，横纵坐标都乘以－1，横纵坐标都加或减等。老师在学生举例的时候动画演示。
5、小组讨论：鱼的变化到底有什么规律？
（1）当横坐标加减时，鱼左右平移；当纵坐标加减时，鱼上下平移。
（2）当横坐标乘除时，鱼横向拉长或压缩；当纵坐标乘除时，鱼纵向拉长或压缩。当横纵坐标都乘除时，鱼变大或缩小，形状不变。
（3）当横坐标乘以-1时，鱼沿y轴翻身，关于y轴对称；当纵坐标乘以-1时，鱼沿x轴翻身，关于x轴对称。
三、巩固练习：
? 1、随堂练习1、2
2、习题5.6的1、2
3、把P(1,2)向上平移3个单位，再向左平移4个单位到达Q，则Q点坐标是____。
四、小结：本节你有哪些收获？鱼是如何变化的？
五、课堂小测：
在△ABC中，三个顶点的坐标分别为 A(-5，0)，B(4，0)，C(2，5)， (1)将△ABC沿x轴正方向平移2个单位长度，再沿y轴沿负方向平移1个单位长度得到△EFG。 ①求△EFG的三个顶点坐标。 ②求△EFG的面积 (2)把△ABC的各顶点的纵坐标乘以2，横坐标乘以3，得到△PMN，则这个三角形的面积是多少？
六、作业布置： 配套练习
七、自我评价
11.4 函数与图象（一）
教师寄语：只有不断总结，才有新的收获.
学习目标：
1、知道函数图象的意义；
2、能画出简单函数的图象，会列表、描点、连线；
3、能从图象上由自变量的值求出对应的函数的近似值。
教学过程：
一、知识准备
1．什么叫函数？
2．什么叫平面直角坐标系？
3．如果点A的横坐标为3，纵坐标为5，请用记号表示A（3，5）.
4．如果已知一个点的坐标，可在坐标平面内画出几个点？反过来，如果坐标平面内的一个点确定，这个点的坐标有几个？这样的点和坐标的对应关系，叫做什么对应？
二、自主学习
学生自主观察图11—12，回答以下问题：
1. 根据图11—12，找出原点、横轴和纵轴，说出横轴和纵轴上的刻度，指出它们所代表的实际意义
2. 认真思考教材57页提出的6个问题，并作出回答。
3. 什么叫做图像法？
4. 我们已经知道，函数关系可以用解析式表示，像y=x-1就表示以x 为自变量时，y是x的函数。这个函数关系中，y与x的对应关系，我们还可通过在坐标平面内画出图象的方法来表示。
1.给定自变量x的一些值，求出对应的y值，并填表：
x -2 -1 0 1 2
y
2.对于表中的每一组对应值，以x值作为点的横坐标，以对应的y值作为点的纵坐标，便可画出一个点。也就是由表中给出的有序实数对，在直角坐标系中描出相应的点。
3. 按照自变量由小到大的顺序把描出的点顺次连结起来。
这样，就得到了函数y=x-1的图象。
总结：用描点法画函数的图像的步骤是什么？
三、合作探究
1、已知函数式y=-2x。用列表(x取-2,-1,2,1,2),描点，连线的程序，画出它的图象。
2、想一想：下列各点哪些在函数y=x-1的图象上？为什么？
A(-1.5,-2.5) B(100,99) C(-10,-9) D(80,81)
四、课堂练习
1.教科书60页练习1、2题
2.画出下列函数的图象：
（1）y=-3x;(2)y=-3x+2; (3)y=-3x-3
五、课堂达标检测
配套练习册
六、课堂小结
1. 到现在，我们已经学过了几种表示函数关系的方法？
2.通过这节课的学习，你有什么收获？还有什么疑惑？
七、布置作业
习题11.4A组1、3题
八、自我评价
项目 等级 A B C D
掌握知识的情况
参与活动的积极性
给自己一句鼓励的话
11.4函数与图像（二）
一、学习目标
　　1、知道函数图象的意义；
　 2、能画出简单函数的图象，会列表、描点、连线；
3、能从图像上由自变量的值求出对应的函数的近似值.
二、教学重点和难点
　重点：认识函数图象的意义，会对简单的函数列表、描点、连线画出函数图象.
　难点：对已知图象能读图、识图，从图象解释函数变化关系.
三、学习过程
　(一)自主预习
　　1._______________________________________________叫函数
　　2. _____________________________________________叫平面直角坐标系
　　3.在坐标平面内，______________叫点的横坐标 ___________________叫点的纵坐标 　　
　　4.如果点A的横坐标为3，纵坐标为5，请用记号表示点A( ，).
　　5.请在坐标平面内画出A点.
6.如果已知一个点的坐标，可在坐标平面内画出几个点 反过来，如果坐标平面内的一个点确定，这个点的坐标有_______个 这样的点和坐标的对应关系，叫做什么对应 　
　(二)自主学习
　　 前几节课已经知道，函数关系可以用解析式表示.像y=2x+1就表示以x为自变量时，y是x的函数.
　　 这个函数关系中，y与x的对应关系，我们还可以用在坐标平面内画出图象的方法表示.
　　具体做法是：
　　第一步：列表.(写出自变量x与函数值的对应表)先确定x的若干个值，然后填入相应的y值.
(这种用表格表示函数关系的方法叫做列表法)
　　第二步：描点，对于表中的每一组对应值，以x值作为点的横坐标，以对应的y值作为点的纵坐标，便可画出一个点.也就是由表中给出的有序实数时，在直角坐标中描出相应的点.
　　第三步：连线，按照横坐标由小到大的顺序把相邻两点用线段连结起来，得到的图形就是函数式y=2x+1图象.
（三）、典例分析：
例、在同一直角坐标系中画出下列函数式的图像：
　　(1) y=-3x; (2)y=-3x+2; (3) y=-3x-3.
分析：按照列表、描点、连线三步操作.
解：
它们的图象分别是图13-25中的(1)，(2)，(3).
　　
（四）、练习巩固：　　已知函数式y=-2x.用列表(x取-2，-1，0，1，2)，描点，连线的程序，画出它的图象.
(五)、小结
表示函数关系的方法有三种：
　　1.解析式法——用数学式子表示函数关系.
　　2.列表法——通过列表给出函数y与自变量x的对应关系.
　　3.图象法——把自变量x作为点的横坐标，对应的函数值y作为点的纵坐标，这三种表示函数的方法各有优缺点.
　　1.解析法表示函数关系
优点与缺点：____________________________________________________
　　2.列表法表示函数关系
优点与缺点：______________________________________________________
3.图象法表示函数
优点与缺点__________________________________
（六）、当堂达标
1.在图13-27中，不能表示函数关系的图形有( ).
A (a),(b),(c) B(b),(c),(d) C (b),(c)(e) D(b),(d),(e)
2.矩形的周长是12cm，设矩形的宽为x(cm),面积为y(cm2).
　　(1) 以x为自变量，y为x的函数，写出函数关系式，并在关系式后面注明x的取值范围；
　　
(2) 列表、描点、连线画出此函数的图象.
　
3.(1) 画出函数y=- x+2的图象(在-4与4之间，每隔1取一个x值，列表；并在直角坐标系中描点画图)；
　　
(2) 判断下列各有序实数对是不是函数y=- x+2的自变量x与函数y的一对对应值，如果是，检验一下具有相应坐标的点是否在你所画的函数图像上：（1，1），（2，0），（3，1），（0，2），（-1，3）　 　
　
4.画出下列函数的图象：　　 (1) y=4x-1; (2)y=4x+1.
（七）、布置作业：配套练习册
四、自我评价
11.5 一次函数和它的图象(第一课时)
教师寄语：当学习方法正确时，成绩是时间的正比例函数。
教学目标
1、理解正比例函数、一次函数的概念。
2、会根据数量关系，求正比例函数、一次函数的解析式。
3、会求一次函数的值。
教学重点与难点
教学重点：一次函数、正比例函数的概念和解析式。
教学难点：求正比例、一次函数的解析式。
教学方法：合作、交流
教学过程：
一、自主学习：（看谁做得好!）
1、阅读课本第62页，写出列车离开浦东机场的距离和时间的关系： 。
2、比较下列各函数，它们有哪些共同特征： 。
3、总结一次函数、正比例函数的定义：
二、合作探究：
（1）作为一次函数的解析式，其中中，哪些是常量，哪些是变量？哪一个是自变量，哪一个是自变量的函数？其中符合什么条件？
（2）在什么条件下，为正比例函数？
三、当堂练习：做一做（初试身手！）
下列函数中，哪些是一次函数？哪些是正比例函数？系数和常数项的值各为多少？
四、典例解析：（看那个组讲得好!）
例1：课本第63页，让二人到黑板上做。其他同学在下面做。
四、当堂练习：（再试身手！）
课本第63页：练习1、2.
五、课堂快餐：（三试身手！）
求出下列各题中与之间的关系，并判断是否为的一次函数，是否为正比例函数：
1、某农场种植玉米，每平方米种玉米6株，玉米株数与种植面积之间的关系。
2、正方形周长与面积之间的关系。
六、链接中考：（2007杭州）假定某种储蓄的月利率是0.16%，存入1000元本金后。本息总钱与所存月数之间的关系是
七、课堂小结（看那个组收获多!）
这节课我的收获是：
我不明白地方是：
八、当堂达标（唯旗必夺！）
1.已知若是的正比例函数，求的值。
2.已知是的一次函数，当时，；当时，
（1）、求关于的一次函数关系式。（2）、求当时，的值。
3、按国家现行有关个人所得税的规定，月工资超出2000元的部分交个人所得税，计算办法：超出2000元的数额若不超过500元的税率为5%，超过500元至2000元部分的税率为10%，设全月工资额为X元，且2000（1）、求关于的函数解析式。
（2）、小明妈妈的工资为每月2600元，小聪妈妈的工资为每月2800元。问她俩每月应纳个人所得税多少元？
九、作业：课本P65第1题
十、自我评价
11.5 一次函数和它的图象(第2课时)
教师寄语：只要善于发现，生活中处处有数学。
教学目标
1、通过具体操作，感受一次函数的图象是一条直线；
2、正确地画出一次函数的图象，探究一次函数的性质，体验学习的乐趣
3．在现实情境中会列一次函数解析式并画出其图象解决实际实际问题。
教学重点与难点
教学重点：了解一次函数的图象是一条直线并会画一次函数的图象。
教学难点：画一次函数的图象选点的技巧。　
教学方法：观察、比较、合作、交流、.
教学过程：
一、温故知新：感受一次函数的图象（看那个组想得全!）
某地1千瓦·时电费为0.8元，用公式法表示电费y（元）与所用的电x（千瓦时）之间的函数关系式是： ，
你能画出这个函数的图象吗？
学生活动：在教师的指导下，学生有序地动手操作实践。
二、自主学习（初试身手！）
画出一次函数y=2x+1的图象
学生活动：学生在练习本上独立完成，充分讨论有什么简单方法？
归纳总结：一般地y=kx+b (k≠0),通常选取它与两轴的交点（0，b），(-b/k,0),即横纵坐标为0 的点，当然，选其它在象限内的点也可以。
三、学以致用，范例分析（看那个组讲得好!）
P64例2
教师活动：引导学生积极分析和思考，针对答题情况师生共同评判；
学生活动：鼓励学生在练习本上独立完成将解答与同伴交流，指定一名学生上台板演。
四、随堂练习：（再试身手！）
画出正比例函数y=-2x的图象
学生活动：在练习本上独立完成，一名学生上台板演，教师查视全体同学练习的情况。
教师活动：教师与学生共议，怎样简单地画正比例函数的图像？
五、合作探究：阅读课本第64页，组内合作总结一次函数的性质：
六、课堂快餐：（三试身手！）
1、求直线y=-x+5与x轴、y轴交点的坐标是（ ）、（ ）
2、函数y=-4x+2的图像经过点（ ）和（ ）。
3、我国某地区现有人工造林面积12万顷，规划今后10年新增造林61000—62000公顷。请估算6年后该地区的造林总面积达到多少公顷？
七、课堂小结：
本节课学习了一次函数的图象是一条直线，会用两点法作其图象，对具体问题会用一次函数的相关知识求解。
八、当堂检测：（唯旗必夺！）
1、函数y=-2x+3随着x的增大而
2、函数y=2x-5的图像与x、y轴的交点坐标是 。
3、画出函数y=-3x+1的图像。
九、作业：课本P45习题2。2
十、自我评价
第（1）题图
第（2）题图
第1题图
学校
北
超市
第3题图
PAGE
1