平方差公式说课
图片预览








文档简介
课件24张PPT。(a+b)(a?b)=a2?b215.2.1平方差公式说课1、教材的地位、作用及前后联系:
平方差公式这一内容是在学生学习了一般的整式乘法之后提出的。平方差公式是特殊的整式乘法,是进一步学习因式分解、分式运算和代数式的变形等知识的重要基础,它作为一种最基本的公式在初中数学中应用十分广泛。一.教材分析
2、教学内容:
本节课的教学内容可以分为三点:
(1)平方差公式的推导
(2)平方差公式的几何论证
(3)平方差公式的应用?3、从学生学习过程的角度看? 学生刚学过多项式的乘法,已具备学习并运用平方差公式的知识结构,通过创设问题情境,让学生在探究相应问题的过程中,建立公式并运用公式,从而拓展学生知识技能结构是完全可能的。?
5、教学重点难点和关键
?
重点:平方差公式的推导和应用
难点:灵活运用平方差公式计算
关键:理解公式中字母的含义返回1、教学方法:
《新课标》强调“让学生经历数学知识的形成与应用过程,充分调动学生思维的主动性、积极性。 ”根据这样的原则和所要完成的教学目标,我的教学模式是“创设情境——探究新知——应用与拓展”。这一教法不但符合教材特点,而且能够充分发挥教师的主导作用和学生的主体作用。 二.教法和学法2、教学手段:
利用多媒体帮助学生突破难点,同时也提高了教学效率,激发学生的兴趣。 返回3、学法指导
有效的数学学习方法不能单纯地依赖模仿与记忆,教师应引导学生主动地参与观察、实验、猜想、验证、交流等数学活动,使学生的学习模式为“自主探索——合作交流——再发明、再发现”,从而增强自学能力.(一)、创设情境:
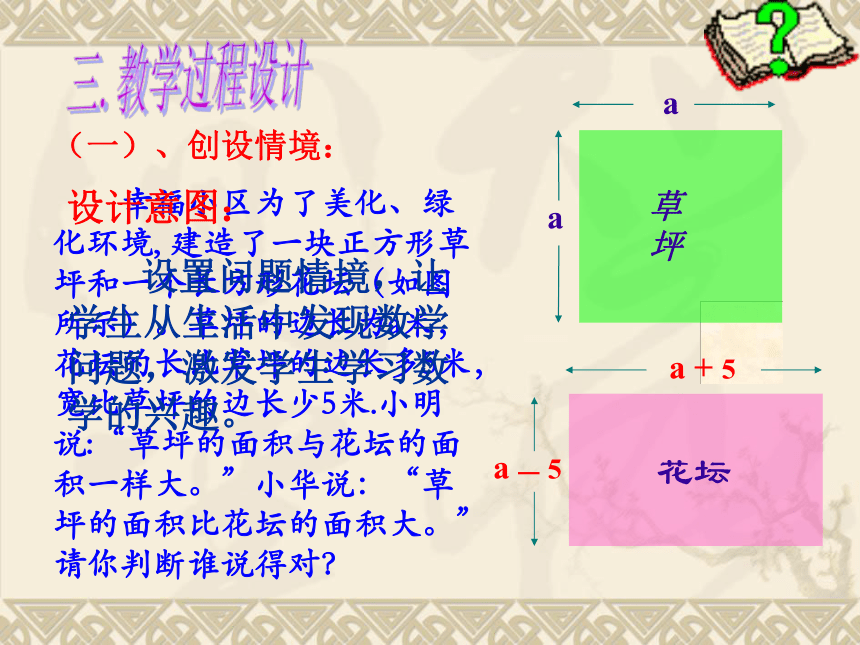
幸福小区为了美化、绿化环境, 建造了一块正方形草坪和一个长方形花坛(如图所示)。草坪的边长为a米,花坛的长比草坪的边长多5米,宽比草坪的边长少5米.小明说:“草坪的面积与花坛的面积一样大。”小华说:“草坪的面积比花坛的面积大。”请你判断谁说得对? 设计意图:
设置问题情境,让学生从生活中发现数学问题,激发学生学习数学的兴趣。 三.教学过程设计(二).探究新知: 1、复习提问: 我们已经学习了多项式乘法,怎样用字母表示多项式的乘法法则呢? (a+b)(m+n)=am+an+bm+bn(45+15)(45--15) = 452-1522、计算下列多项式的积,你能发现什么规律?
(1)(x+1)(x-1)
(2)(m+2)(m-2)
(3)(2x+1)(2x-1)3.小组内讨论
观察第2题的算式和结果,你有什么发现?把你的发现在小组内交流,试试看,能否把你的发现用式子表示出来? 左边是两个数的和与这两个数的差的积,
右边是这两个数的平方差。 你发现规律了吗? (1)如图①边长为a的大正方形中有一个边长为b 的小正方形。请表示图中阴影部分的面积。4.拼图验证 (2)晶晶将阴影部分拼成了一个如图②的长方形,这个长方形的长和宽分别是多少?你能把它的面积表示出来吗?
(3)从以上两小题中,你有什么发现? ①②设计意图: 设计知识“最近发展区”——多项式乘法,为推导平方差公式作好铺垫;
让学生经历公式的探索过程,有意识的培养学生观察、对比、分析、抽象和概括的能力,使学生真正理解公式的来源和本质;
利用拼图的趣味性和直观性进行验证,一方面有助于渗透数形结合的思想方法,另一方面可以调动学生的学习热情。 平方差公式: (a+b)(a-b)=
即:两个数的和与这两个数的差的积,等于这两个数的平方差. (三)、归纳新知 a2—b2
设计意图:通过分析、归纳,使学生初步理解平方差公式的特征。 (1)(3x+2)(3x-2)
(2)(b+2a)(b-2a)
(3)(-x+2y)(-x-2y)
(4)(ab+8)(ab-8)例1、利用平方差公式计算:(四)、运用新知 =(3x)2-22=9x2-4(1)(3x+2)(3x-2) (2)(b+2a)(b-2a)(3)(-x+2y)(-x-2y)(4)(ab+8)(ab-8)=(b)2-(2a)2=b2-4a2=(-x)2-(2y)2=x2-4y2=(ab)2-82=a2b2-64注意:公式中a﹑ b可以是字母,也可以是代数式。1﹑判断正误:如果错误,应怎样改正?
( 1 ) (-a-b)(a-b)=-a2+b2 ( )
( 2 ) (-a+b)(-a-b)=-a2-b2 ( )
( 3 ) (2x+3)(2x-3)=2x2-9 ( )
( 4 ) (3x-1)(-3x-1)=9x2-1 ( ) 请说明原因(五)、反馈练习(小组讨论、竞赛的形式) 2、下列各式哪些能用平方差公式计算?怎样用?
1) (a-b+c)(a-b-c)
2) (y-z)(-y+z)设计意图:
通过全班练习、合作交流,使学生深刻理解:题目能否运用平方差公式,关键是识别两个数,如果是两个数的和与差相乘,就可以按公式计算。为了识别这两个数,有时需要变形。 (六)、应用拓展 (小组讨论、竞赛的形式)
例2﹑计算下列各题:
(1)102×98 (转化思想)
(2) (y+2)(y-2) — (y–1)(y+5) (综合运用)
(3) (m+2)2-(m-1)2 (逆向思维训练) 回放创设情境中的问题 幸福小区为了美化、绿化环境, 建造了一块正方形草坪和一个长方形花坛(如图所示)。草坪的边长为a米,花坛的长比草坪的边长多5米,宽比草坪的边长少5米.小明说:“草坪的面积与花坛的面积一样大。”小华说:“草坪的面积比花坛的面积大。”请你判断谁说得对?设计意图: 例2包括3道小题,第1题体现了“转化思想”;第2题是培养学生综合运用公式的能力;第3题是逆向思维训练。
另外,解决本节课开始时提出的问题,前后呼应。让学生共享成功的喜悦。 (七)、反思小结 (由同学们自已总结)
1、本节你学到了什么?
2、本节课你有何收获?
3、你们还有什么疑惑? 设计意图:
通过小结明确本节的主要内容、思想和方法,培养学生善于反思的良好习惯。 (八)布置作业 P156习题15.2中的复习巩固第1题,
P157综合运用第3题(1)(2)
(选做): (1) 计算(x+y)(x-y)(x2+y2)
(2) 观察式子( )( )
在括号内填入怎样的式子才能用平方差公式计算.设计意图:
通过课后完成作业使学生巩固本节知识。设计选做题是为了使“不同的人在数学上得到不同的发展”。 谢谢光临指导
平方差公式这一内容是在学生学习了一般的整式乘法之后提出的。平方差公式是特殊的整式乘法,是进一步学习因式分解、分式运算和代数式的变形等知识的重要基础,它作为一种最基本的公式在初中数学中应用十分广泛。一.教材分析
2、教学内容:
本节课的教学内容可以分为三点:
(1)平方差公式的推导
(2)平方差公式的几何论证
(3)平方差公式的应用?3、从学生学习过程的角度看? 学生刚学过多项式的乘法,已具备学习并运用平方差公式的知识结构,通过创设问题情境,让学生在探究相应问题的过程中,建立公式并运用公式,从而拓展学生知识技能结构是完全可能的。?
5、教学重点难点和关键
?
重点:平方差公式的推导和应用
难点:灵活运用平方差公式计算
关键:理解公式中字母的含义返回1、教学方法:
《新课标》强调“让学生经历数学知识的形成与应用过程,充分调动学生思维的主动性、积极性。 ”根据这样的原则和所要完成的教学目标,我的教学模式是“创设情境——探究新知——应用与拓展”。这一教法不但符合教材特点,而且能够充分发挥教师的主导作用和学生的主体作用。 二.教法和学法2、教学手段:
利用多媒体帮助学生突破难点,同时也提高了教学效率,激发学生的兴趣。 返回3、学法指导
有效的数学学习方法不能单纯地依赖模仿与记忆,教师应引导学生主动地参与观察、实验、猜想、验证、交流等数学活动,使学生的学习模式为“自主探索——合作交流——再发明、再发现”,从而增强自学能力.(一)、创设情境:
幸福小区为了美化、绿化环境, 建造了一块正方形草坪和一个长方形花坛(如图所示)。草坪的边长为a米,花坛的长比草坪的边长多5米,宽比草坪的边长少5米.小明说:“草坪的面积与花坛的面积一样大。”小华说:“草坪的面积比花坛的面积大。”请你判断谁说得对? 设计意图:
设置问题情境,让学生从生活中发现数学问题,激发学生学习数学的兴趣。 三.教学过程设计(二).探究新知: 1、复习提问: 我们已经学习了多项式乘法,怎样用字母表示多项式的乘法法则呢? (a+b)(m+n)=am+an+bm+bn(45+15)(45--15) = 452-1522、计算下列多项式的积,你能发现什么规律?
(1)(x+1)(x-1)
(2)(m+2)(m-2)
(3)(2x+1)(2x-1)3.小组内讨论
观察第2题的算式和结果,你有什么发现?把你的发现在小组内交流,试试看,能否把你的发现用式子表示出来? 左边是两个数的和与这两个数的差的积,
右边是这两个数的平方差。 你发现规律了吗? (1)如图①边长为a的大正方形中有一个边长为b 的小正方形。请表示图中阴影部分的面积。4.拼图验证 (2)晶晶将阴影部分拼成了一个如图②的长方形,这个长方形的长和宽分别是多少?你能把它的面积表示出来吗?
(3)从以上两小题中,你有什么发现? ①②设计意图: 设计知识“最近发展区”——多项式乘法,为推导平方差公式作好铺垫;
让学生经历公式的探索过程,有意识的培养学生观察、对比、分析、抽象和概括的能力,使学生真正理解公式的来源和本质;
利用拼图的趣味性和直观性进行验证,一方面有助于渗透数形结合的思想方法,另一方面可以调动学生的学习热情。 平方差公式: (a+b)(a-b)=
即:两个数的和与这两个数的差的积,等于这两个数的平方差. (三)、归纳新知 a2—b2
设计意图:通过分析、归纳,使学生初步理解平方差公式的特征。 (1)(3x+2)(3x-2)
(2)(b+2a)(b-2a)
(3)(-x+2y)(-x-2y)
(4)(ab+8)(ab-8)例1、利用平方差公式计算:(四)、运用新知 =(3x)2-22=9x2-4(1)(3x+2)(3x-2) (2)(b+2a)(b-2a)(3)(-x+2y)(-x-2y)(4)(ab+8)(ab-8)=(b)2-(2a)2=b2-4a2=(-x)2-(2y)2=x2-4y2=(ab)2-82=a2b2-64注意:公式中a﹑ b可以是字母,也可以是代数式。1﹑判断正误:如果错误,应怎样改正?
( 1 ) (-a-b)(a-b)=-a2+b2 ( )
( 2 ) (-a+b)(-a-b)=-a2-b2 ( )
( 3 ) (2x+3)(2x-3)=2x2-9 ( )
( 4 ) (3x-1)(-3x-1)=9x2-1 ( ) 请说明原因(五)、反馈练习(小组讨论、竞赛的形式) 2、下列各式哪些能用平方差公式计算?怎样用?
1) (a-b+c)(a-b-c)
2) (y-z)(-y+z)设计意图:
通过全班练习、合作交流,使学生深刻理解:题目能否运用平方差公式,关键是识别两个数,如果是两个数的和与差相乘,就可以按公式计算。为了识别这两个数,有时需要变形。 (六)、应用拓展 (小组讨论、竞赛的形式)
例2﹑计算下列各题:
(1)102×98 (转化思想)
(2) (y+2)(y-2) — (y–1)(y+5) (综合运用)
(3) (m+2)2-(m-1)2 (逆向思维训练) 回放创设情境中的问题 幸福小区为了美化、绿化环境, 建造了一块正方形草坪和一个长方形花坛(如图所示)。草坪的边长为a米,花坛的长比草坪的边长多5米,宽比草坪的边长少5米.小明说:“草坪的面积与花坛的面积一样大。”小华说:“草坪的面积比花坛的面积大。”请你判断谁说得对?设计意图: 例2包括3道小题,第1题体现了“转化思想”;第2题是培养学生综合运用公式的能力;第3题是逆向思维训练。
另外,解决本节课开始时提出的问题,前后呼应。让学生共享成功的喜悦。 (七)、反思小结 (由同学们自已总结)
1、本节你学到了什么?
2、本节课你有何收获?
3、你们还有什么疑惑? 设计意图:
通过小结明确本节的主要内容、思想和方法,培养学生善于反思的良好习惯。 (八)布置作业 P156习题15.2中的复习巩固第1题,
P157综合运用第3题(1)(2)
(选做): (1) 计算(x+y)(x-y)(x2+y2)
(2) 观察式子( )( )
在括号内填入怎样的式子才能用平方差公式计算.设计意图:
通过课后完成作业使学生巩固本节知识。设计选做题是为了使“不同的人在数学上得到不同的发展”。 谢谢光临指导
