二次函数y=ax2的图像和性质

课件19张PPT。二次函数y=ax2的
图象和性质xy26.2.1一. 平面直角坐标系:
1. 有关概念:x(横轴)y(纵轴)o第一象限第二象限第三象限第四象限Pab(a,b)2. 平面内点的坐标:3. 坐标平面内的点与有序
实数对是:一一对应. 坐标平面内的任意一点M,都有唯一一对
有序实数(x,y)与它对应;任意一对有序实数
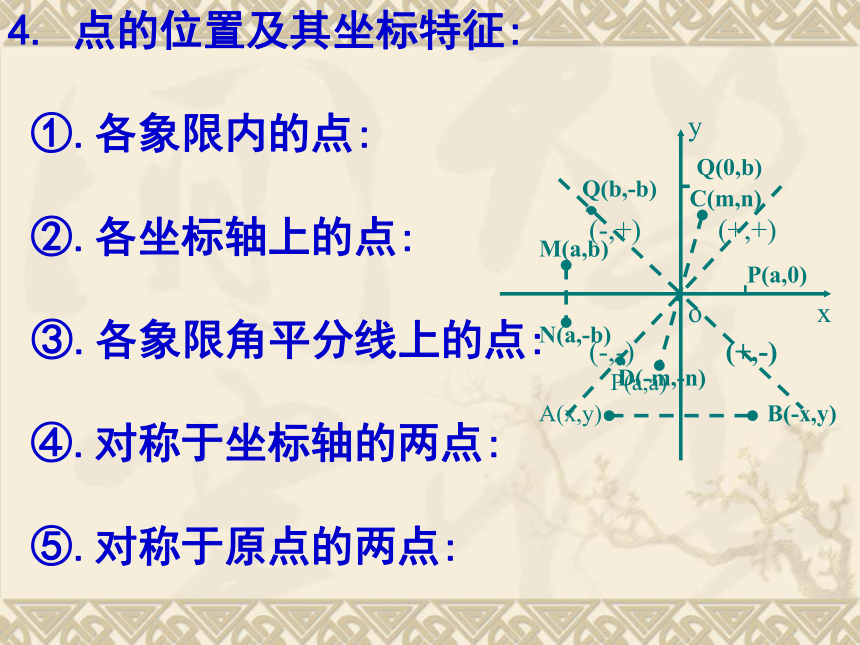
(x,y),在坐标平面内都有唯一的点M与它对应.知识回顾4. 点的位置及其坐标特征:
①.各象限内的点:
②.各坐标轴上的点:
③.各象限角平分线上的点:
④.对称于坐标轴的两点:
⑤.对称于原点的两点:xyo(+,+)(-,+)(-,-)(+,-)P(a,0)Q(0,b)P(a,a)Q(b,-b)M(a,b)N(a,-b)A(x,y) B(-x,y)C(m,n)D(-m,-n)5.一次函数 的图象是_____________；
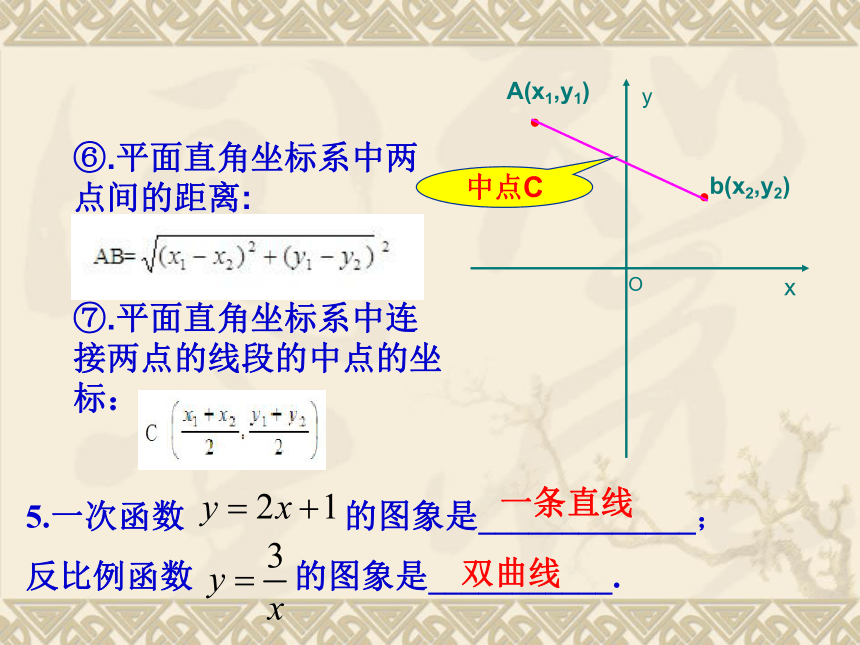
反比例函数 的图象是___________.一条直线双曲线⑥.平面直角坐标系中两点间的距离:
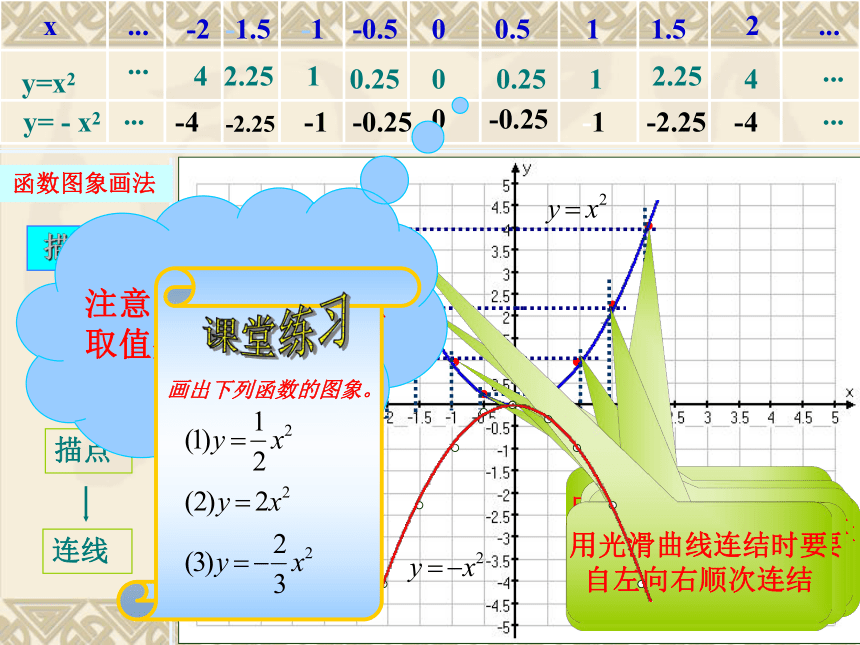
⑦.平面直角坐标系中连接两点的线段的中点的坐标：A(x1,y1)b(x2,y2)中点C问题2：如何画二次函数y=x2的图象呢？问题1：二次函数y=x2的图象是什么呢？合作探究 函数图象画法（描点法）列表描点连线 函数图象画法列表描点连线00.2512.2540.2512.254 描点法用光滑曲线连结时要
自左向右顺次连结用光滑曲线连结时要
自左向右顺次连结用光滑曲线连结时要
自左向右顺次连结用光滑曲线连结时要
自左向右顺次连结用光滑曲线连结时要
自左向右顺次连结用光滑曲线连结时要
自左向右顺次连结用光滑曲线连结时要
自左向右顺次连结用光滑曲线连结时要
自左向右顺次连结用光滑曲线连结时要
自左向右顺次连结0-0.25-1-2.25-4-0.25-1-2.25-4注意：列表时自变量
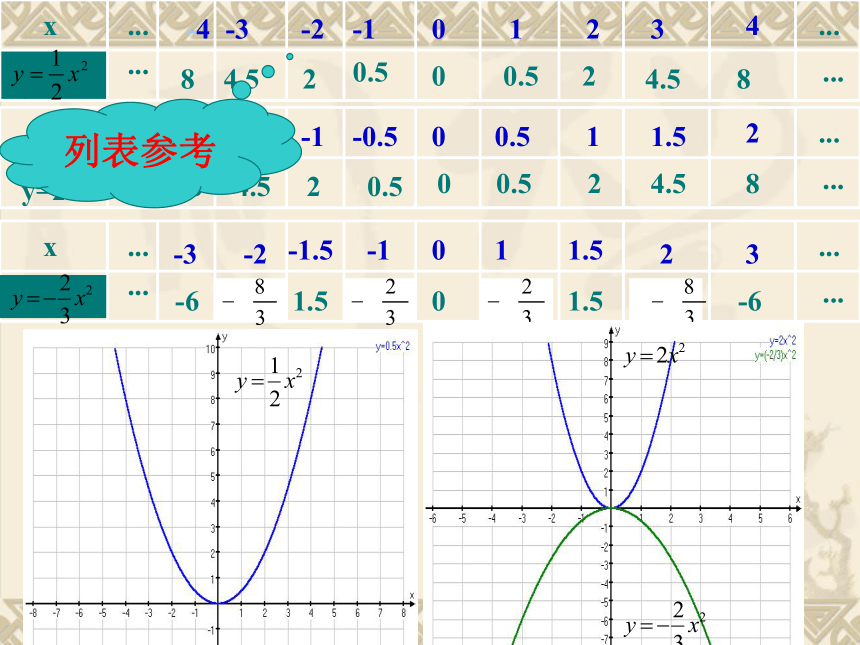
取值要均匀和对称。00.524.580.524.5800.524.580.524.5801.5-61.5-6列表参考二次函数y=ax2的图象形如物体抛射时
所经过的路线，我们把它叫做抛物线。这条抛物线关于y轴
对称，y轴就是它的
对称轴。 这条抛物线关于y轴
对称，y轴就是它的
对称轴。 这条抛物线关于y轴
对称，y轴就是它的
对称轴。 对称轴与抛物线的交点
叫做抛物线的顶点。对称轴与抛物线的交点
叫做抛物线的顶点。对称轴与抛物线的交点
叫做抛物线的顶点。（0，0）（0，0）y轴y轴在x轴的上方（除顶点外）在x轴的下方（除顶点外）向上向下当x=0时，最小值为0。当x=0时，最大值为0。二次函数y=ax2的性质１、顶点坐标与对称轴２、位置与开口方向３、增减性与极值2、练习23、想一想

在同一坐标系内，抛物线y=x2与抛物线
y= -x2的位置有什么关系？ 如果在同一坐标系内
画函数y=ax2与y= -ax2的图象，怎样画才简便？

4、练习4动画演示当a>0时，在对称轴的
左侧，y随着x的增大而
减小。 当a>0时，在对称轴的
右侧，y随着x的增大而
增大。 当a<0时，在对称轴的
左侧，y随着x的增大而
增大。 当a<0时，在对称轴的
右侧，y随着x的增大而
减小。 1、抛物线y=ax2的顶点是原点，对称轴是y轴。2、当a>0时，抛物线y=ax2在x轴的上方（除顶点外），它的开口向上，并且向上无限伸展；
当a<0时，抛物线y=ax2在x轴的下方（除顶点外），它的开口向下，并且向下无限伸展。3、当a>0时，在对称轴的左侧，y随着x的增大而减小；在对称轴右侧，y随着x的增大而增大。当x=0时函数y的值最小。 当a<0时，在对称轴的左侧，y随着x的增大而增大；在对称轴的右侧，y随着x增大而减小，当x=0时，函数y的值最大。二次函数y=ax2的性质2、根据左边已画好的函数图象填空：
（1）抛物线y=2x2的顶点坐标是 ,
对称轴是 ，在 侧，
y随着x的增大而增大；在 侧，
y随着x的增大而减小，当x= 时，
函数y的值最小，最小值是 ,抛物
线y=2x2在x轴的 方（除顶点外）。（2）抛物线 在x轴的 方（除顶点外），在对称轴的
左侧，y随着x的 ；在对称轴的右侧，y随着x的
，当x=0时，函数y的值最大，最大值是 ，
当x 0时，y<0.（0，0）y轴对称轴的右对称轴的左00上下增大而增大增大而减小01、已知抛物线y=ax2经过点A（-2，-8）。
（1）求此抛物线的函数解析式；
（2）判断点B（-1，- 4）是否在此抛物线上。
（3）求出此抛物线上纵坐标为-6的点的坐标。
（4）点 和 在此抛物线上，试比较a和b的大小。解（1）把（-2，-8）代入y=ax2,得
-8=a(-2)2,解出a= -2,所求函数解析式为
y= -2x2.（2）因为 ，所以点B（-1 ，-4）
不在此抛物线上。1、已知抛物线y=ax2经过点A（-2，-8）。
（3）求出此抛物线上纵坐标为-6的点的坐标。
（4）点 和 在此抛物线上，试比较a和b的大小。（3）由-6=-2x2 ,得x2=3,
所以纵坐标为-6的点有两个，它们分别是

解： （4）因为点 和 在抛物线y= -2x2上 所以当 时，
当 时，
因此 mn在对称轴的右边y随x的增大而减小通过本节的学习你有哪些收获呢？家庭作业:教材P6练习1、2、3、4 课堂小结中考语录 一场、两场、三场、四场考试，
最终为了一场中考；
一次、两次、三次、四次痛苦，
最终为了一次微笑。勇攀高峰 画一画：函数y＝x2和y＝-x2、y＝2x2和y＝-2x2、
y＝3x2和y＝-3x2，
（1）你发现它们之间有什么关系呢？（2）你能从函数y＝ax2和y＝－ax2得出什么结论呢？
画一画：(1)函数 ，当a取1、2、3、4 …… 时,
函数的开口大小有什么变化呢？
(2)函数 ，当a取-1、-2、-3、-4 ……时,
函数的开口大小有什么变化呢？