(冀教版九年级上)数学: 29.3 相似三角形(课件)
文档属性
| 名称 | (冀教版九年级上)数学: 29.3 相似三角形(课件) |  | |
| 格式 | rar | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-11-10 13:26:00 | ||
图片预览



文档简介
课件17张PPT。29.3相似三角形 A
B C A’
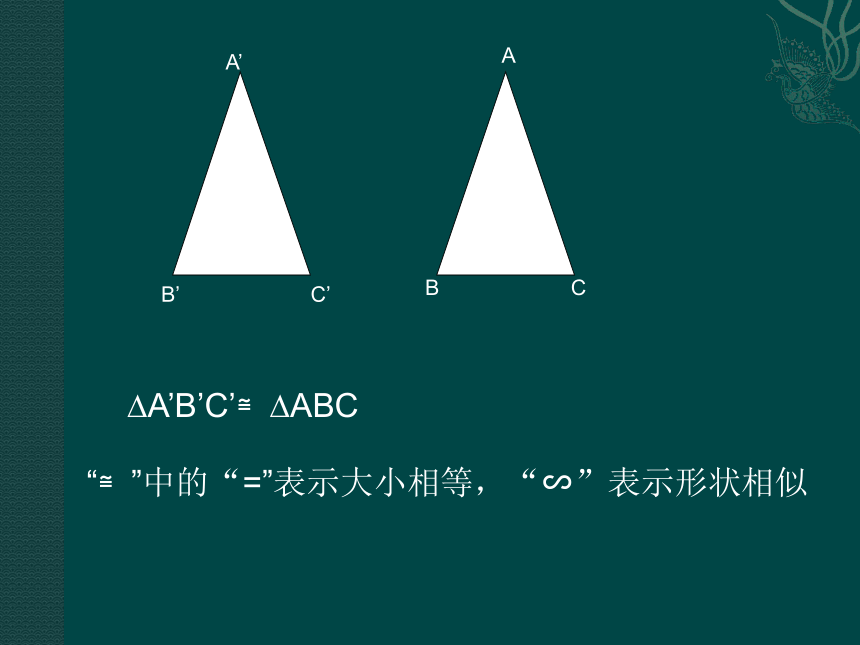
B’ C’?A’B’C’≌?ABC“≌”中的“=”表示大小相等,“∽”表示形状相似相似.∠A′=∠A, ∠B′=∠B, ∠C′=∠C;
对应角相等,对应边成比例的两个三角形,
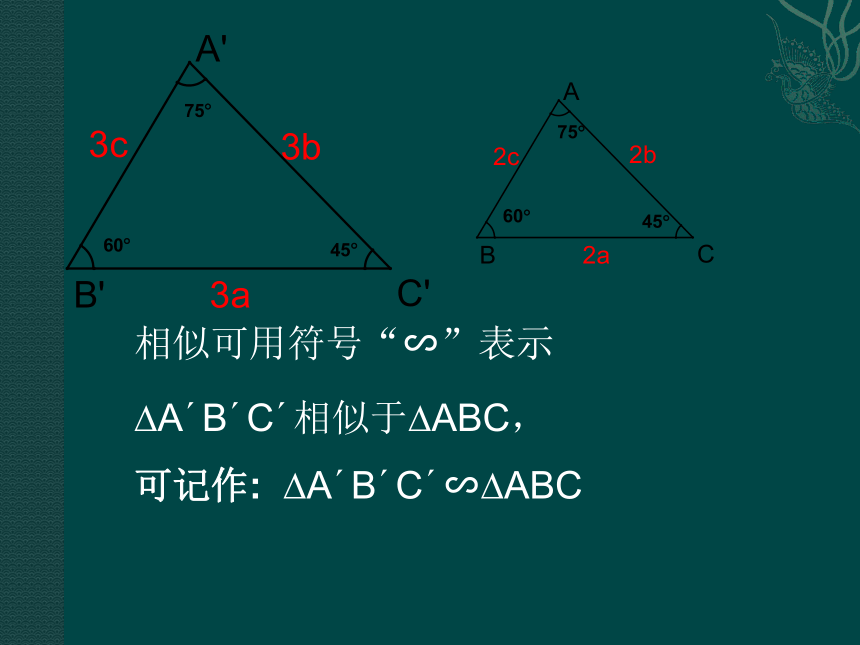
叫做相似三角形 ?A′B′C′相似于?ABC, 可记作: ?A′B′C′∽?ABC相似可用符号“∽”表示
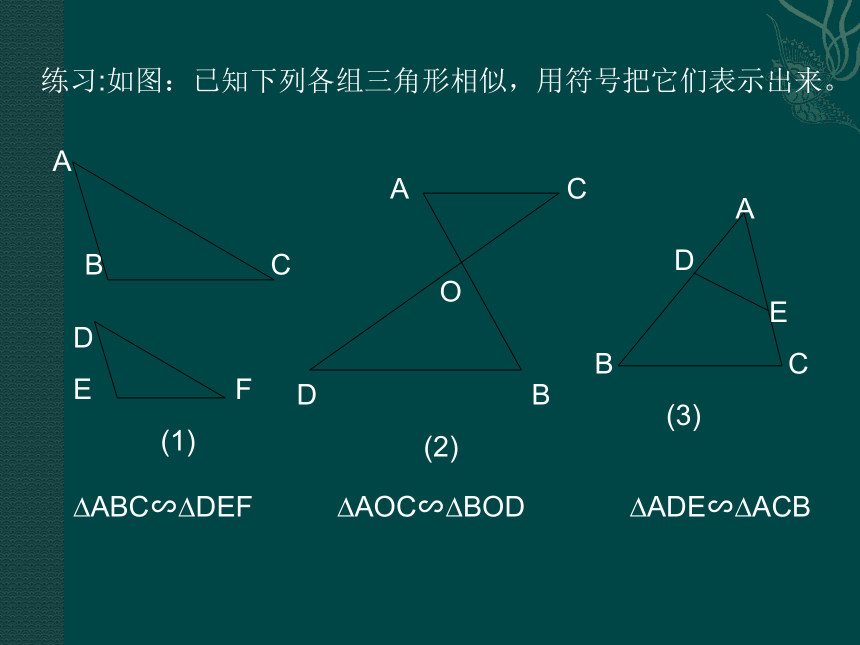
练习:如图:已知下列各组三角形相似,用符号把它们表示出来。A
B CD
E F
(1) A C
O
D B
(2) A
D
E
B C
(3)?AOC∽?BOD?ABC∽?DEF ?ADE∽?ACB练习:A
B CD
E F
(1) ?ABC∽?DEF相似三角形的性质: 相似三角形的对应角相等,对应边成比例。 ∠A=∠D,∠B=∠E,∠C=∠F
A C
O
D B
(2) A
D
E
B C
(3)?AOC∽?BOD ?ADE∽?ACB ∠A=∠B,∠C=∠D,∠AOC=∠BOD∠A=∠A,∠ADE=∠C,∠AED=∠B,
相似三角形的对应边的比,叫做两个相似三角形的相似比
(或相似系数)相似三角形?ABC与?A′B′C′
的相似比是2/3相似三角形?A′B′C′与?ABC
的相似比是3/2 全等三角形的相似比是多少? ∴∴例 如图:在?ABC中,DE∥BC,D、E分别在AB、AC上,
你能得出哪些结论? 例1 如图:在?ABC中,DE∥BC,D、E分别在AB、AC上,
求证:
证明: 过点E作EF//AB交BC于F点。 ∵ DE//BC∴ ∠ADE=∠B,∠AED=∠C又∵ EF//AB∴ DE=BF∴∴∴ ?ADE∽?ABC?ADE∽?ABC又∵∠A=∠A定理:
平行于三角形一边的直线和其它两边(或两边的延长线)
相交,所构成的三角形与原三角形相似。DE//BC?ADE∽?ABC例2 如图,D为?ABC的边AB上的一点,过点D作DE//AC,
交BC于E。已知BE:EC=2:1,AC=6cm,求DE的长 解:∵DE//AC∴?DBE∽?ABC ∴又∵ ∴∴答:DE的长为4cm.练习. 如图, AC与BD交于O点, 且AB//CD, 已知
CO:CA=1:3, CD=5, 求AB的长.思考题? 如图, AB//CD, BD,AC交于点G, F为AB上
一点, DF交AC于E.
求AF与FB的比.小结:1.相似三角形的定义,表示方法,及比例系数.2.相似三角形的性质.3.相似三角形的判定方法.
B C A’
B’ C’?A’B’C’≌?ABC“≌”中的“=”表示大小相等,“∽”表示形状相似相似.∠A′=∠A, ∠B′=∠B, ∠C′=∠C;
对应角相等,对应边成比例的两个三角形,
叫做相似三角形 ?A′B′C′相似于?ABC, 可记作: ?A′B′C′∽?ABC相似可用符号“∽”表示
练习:如图:已知下列各组三角形相似,用符号把它们表示出来。A
B CD
E F
(1) A C
O
D B
(2) A
D
E
B C
(3)?AOC∽?BOD?ABC∽?DEF ?ADE∽?ACB练习:A
B CD
E F
(1) ?ABC∽?DEF相似三角形的性质: 相似三角形的对应角相等,对应边成比例。 ∠A=∠D,∠B=∠E,∠C=∠F
A C
O
D B
(2) A
D
E
B C
(3)?AOC∽?BOD ?ADE∽?ACB ∠A=∠B,∠C=∠D,∠AOC=∠BOD∠A=∠A,∠ADE=∠C,∠AED=∠B,
相似三角形的对应边的比,叫做两个相似三角形的相似比
(或相似系数)相似三角形?ABC与?A′B′C′
的相似比是2/3相似三角形?A′B′C′与?ABC
的相似比是3/2 全等三角形的相似比是多少? ∴∴例 如图:在?ABC中,DE∥BC,D、E分别在AB、AC上,
你能得出哪些结论? 例1 如图:在?ABC中,DE∥BC,D、E分别在AB、AC上,
求证:
证明: 过点E作EF//AB交BC于F点。 ∵ DE//BC∴ ∠ADE=∠B,∠AED=∠C又∵ EF//AB∴ DE=BF∴∴∴ ?ADE∽?ABC?ADE∽?ABC又∵∠A=∠A定理:
平行于三角形一边的直线和其它两边(或两边的延长线)
相交,所构成的三角形与原三角形相似。DE//BC?ADE∽?ABC例2 如图,D为?ABC的边AB上的一点,过点D作DE//AC,
交BC于E。已知BE:EC=2:1,AC=6cm,求DE的长 解:∵DE//AC∴?DBE∽?ABC ∴又∵ ∴∴答:DE的长为4cm.练习. 如图, AC与BD交于O点, 且AB//CD, 已知
CO:CA=1:3, CD=5, 求AB的长.思考题? 如图, AB//CD, BD,AC交于点G, F为AB上
一点, DF交AC于E.
求AF与FB的比.小结:1.相似三角形的定义,表示方法,及比例系数.2.相似三角形的性质.3.相似三角形的判定方法.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
