(冀教版九年级上)数学: 32.2 平行四边形的性质定理和判定定理及其证明(课件)
文档属性
| 名称 | (冀教版九年级上)数学: 32.2 平行四边形的性质定理和判定定理及其证明(课件) |

|
|
| 格式 | rar | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-11-10 00:00:00 | ||
图片预览


文档简介
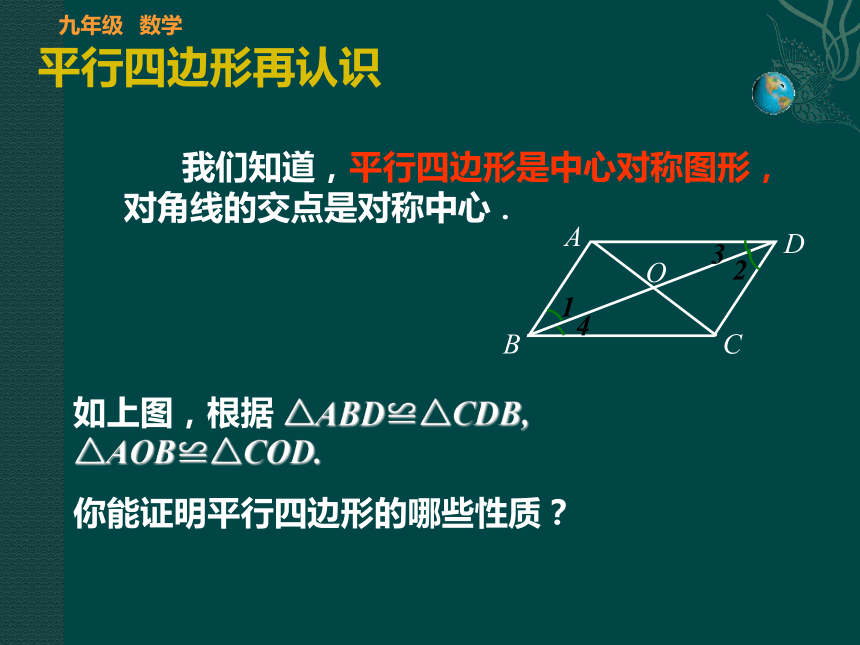
课件6张PPT。32.2 平行四边形的性质定理和判定定理及其证明九年级 数学平行四边形再认识 我们知道,平行四边形是中心对称图形,对角线的交点是对称中心.如上图,根据 △ABD≌△CDB, △AOB≌△COD.
你能证明平行四边形的哪些性质?
4123O平行四边形的两个性质:
定理1 平行四边形的对边相等
定理2平行四边形的对角相等
在△ABD和△CDB 中,
∵ AB∥CD, AD∥BC,
∴ ∠1=∠2, ∠3=∠4 .
又∵ BD=DB, ∴△ABD≌△CDB
∴AB=CD,AD=CB, ∴ ∠BAD=∠DCB.
同理,我们可以证明△ABC≌△CDA,得到∠ABC=∠CDA.九年级 数学一起探究动手做一做如图□ ABCD 的两条对角线AC、BD相交于点O(1) 图中有哪些三角形是全等的?有哪些线段是相等的?OA =OC OB=OD(2) 能设法验证你的结论吗?你可以用证明的方法,也可以用复制纸片并借助旋转的方法.其中九年级 数学证明: ∵在□ABCD中, AD∥BC
∴∠1=∠2, 又AO=CO,AD=CB.
在△AOE和△COF 中,
∵ ∠1=∠2, AO=CO, ∠AOE=∠COF,
∴ △AOE≌△COF. ∴OE=OF,AE=CF.
∴DE=AD – AE=CB – CF=BF.
例题赏析 如图,在□ABCD中,O为对角线AC、BD的交点, 直线EF过点O,交AD于点E,交BC与点F.
求证:OE=OF,AE=CF,DE=BF . 九年级 数学 已知:如图,在□ ABCD中,E,F分
别是BC,AD上的点,且BE=DF.
求证:AE=CF. 练习九年级 数学
你能证明平行四边形的哪些性质?
4123O平行四边形的两个性质:
定理1 平行四边形的对边相等
定理2平行四边形的对角相等
在△ABD和△CDB 中,
∵ AB∥CD, AD∥BC,
∴ ∠1=∠2, ∠3=∠4 .
又∵ BD=DB, ∴△ABD≌△CDB
∴AB=CD,AD=CB, ∴ ∠BAD=∠DCB.
同理,我们可以证明△ABC≌△CDA,得到∠ABC=∠CDA.九年级 数学一起探究动手做一做如图□ ABCD 的两条对角线AC、BD相交于点O(1) 图中有哪些三角形是全等的?有哪些线段是相等的?OA =OC OB=OD(2) 能设法验证你的结论吗?你可以用证明的方法,也可以用复制纸片并借助旋转的方法.其中九年级 数学证明: ∵在□ABCD中, AD∥BC
∴∠1=∠2, 又AO=CO,AD=CB.
在△AOE和△COF 中,
∵ ∠1=∠2, AO=CO, ∠AOE=∠COF,
∴ △AOE≌△COF. ∴OE=OF,AE=CF.
∴DE=AD – AE=CB – CF=BF.
例题赏析 如图,在□ABCD中,O为对角线AC、BD的交点, 直线EF过点O,交AD于点E,交BC与点F.
求证:OE=OF,AE=CF,DE=BF . 九年级 数学 已知:如图,在□ ABCD中,E,F分
别是BC,AD上的点,且BE=DF.
求证:AE=CF. 练习九年级 数学
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
