(冀教版九年级上)数学: 32.3 矩形、菱形的性质定理和判定定理及其证明(课件)
文档属性
| 名称 | (冀教版九年级上)数学: 32.3 矩形、菱形的性质定理和判定定理及其证明(课件) |  | |
| 格式 | rar | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-11-10 13:25:00 | ||
图片预览



文档简介
课件9张PPT。32、3矩形、菱形的性质定理和判定定理及其证明矩形的性质 通过第二十二章的学习,我们发现矩形是一种特殊的平行四边形,它最大的特点就是四个角都是直角,对角线相等。已知:如图,四边形ABCD是矩形, ∠A=90°.
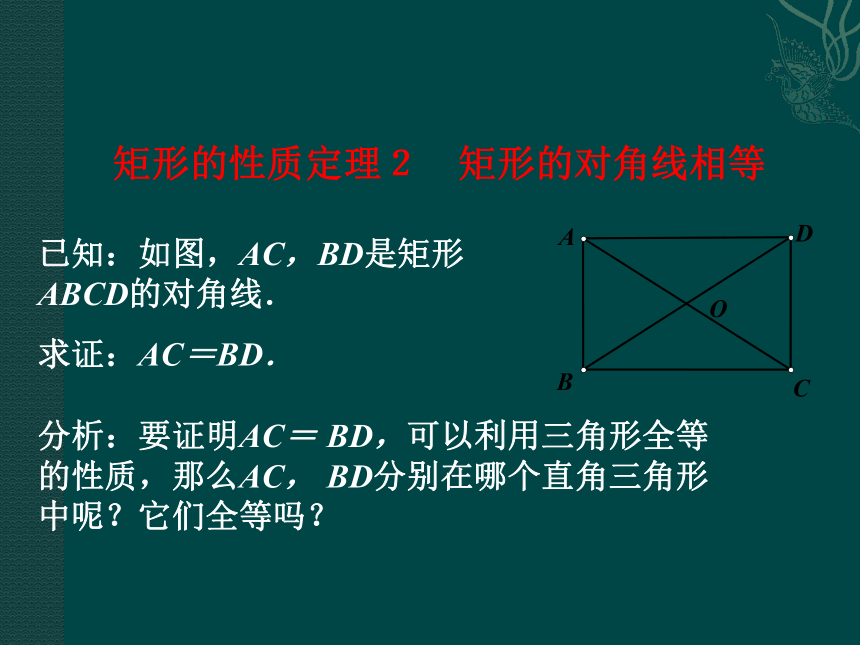
求证: ∠B=∠C =∠D =90°.矩形的性质定理1 矩形的四个角都是直角 矩形的性质定理2 矩形的对角线相等已知:如图,AC,BD是矩形ABCD的对角线.
求证:AC=BD.分析:要证明AC= BD,可以利用三角形全等的性质,那么AC, BD分别在哪个直角三角形中呢?它们全等吗?观察与思考已知:如图,在矩形ABCD中,
对角线AC与BD相交于点O.
1.OA=OB吗?为什么?
2.OB与AC有什么数量关系?由此,我们可以得到:
推论 直角三角形斜边上的中线等于斜边的一半.结论:对角线相等的平行四边形是矩形.探索:AB=DC,BD=CA,AD=DA∴△BAD≌△CDA(SSS)∴∠BAD=∠CDA∵AB∥CD∴∠BAD +∠CDA=180° ∴∠BAD=90° ∴四边形ABCD是矩形(有一个内角是直角的平行四边形是矩形)对角线相等的平行四边形是矩形吗?猜想加证明判定定理:有三个角是直角的四边形是矩形.已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.分析:利用同旁内角互补,两直线平行来证明四边形是平行四边形,可使问题得证.证明:∵ ∠A=∠B=∠C=90°,∴∠A+∠B=180°,∠B+∠C=180°.∴AD∥BC,AB∥CD.求证:四边形ABCD是矩形.∴四边形ABCD是平行四边形.∴四边形ABCD是矩形.练习自我诊断 1、能够判断一个四边形是矩形的条件是( )
A 对角线相等 B 对角线垂直
C对角线互相平分且相等 D对角线垂直且相等
2、矩形的一组邻边长分别是3cm和4cm,则它的对角线长是 cm
3、如图,直线EF∥MN,PQ交EF、MN于A、C两点,AB、CB、CD、AD分别是∠ EAC、 ∠ MCA、 ∠ ACN、 ∠ CAF的角平分线,则四边形ABCD是( )
A 菱形 B 平行四边形
C 矩形 D 不能确定 1、如图,矩形ABCD的对角线AC、BD相交于O,∠BOC=2 ∠ AOB,若AC=6cm,试求AB的长.
2、如图,O是菱形ABCD对角线的交点,作DE∥AC,CE∥BD,DE、CE交于点E,四边形CEDO是矩形吗?说出你的理由.随堂练已知:如图,四边形ABCD是平行四边形,P是CD上的一点,且AP和BP分别分别平分∠DAB和∠CBA,QP∥AD,交AB于点Q.
(1).求证:AP⊥PB;
(2).如果AD=5cm,AP=8cm,那么AB的长是多少? △APB的面积是多少?随堂练
求证: ∠B=∠C =∠D =90°.矩形的性质定理1 矩形的四个角都是直角 矩形的性质定理2 矩形的对角线相等已知:如图,AC,BD是矩形ABCD的对角线.
求证:AC=BD.分析:要证明AC= BD,可以利用三角形全等的性质,那么AC, BD分别在哪个直角三角形中呢?它们全等吗?观察与思考已知:如图,在矩形ABCD中,
对角线AC与BD相交于点O.
1.OA=OB吗?为什么?
2.OB与AC有什么数量关系?由此,我们可以得到:
推论 直角三角形斜边上的中线等于斜边的一半.结论:对角线相等的平行四边形是矩形.探索:AB=DC,BD=CA,AD=DA∴△BAD≌△CDA(SSS)∴∠BAD=∠CDA∵AB∥CD∴∠BAD +∠CDA=180° ∴∠BAD=90° ∴四边形ABCD是矩形(有一个内角是直角的平行四边形是矩形)对角线相等的平行四边形是矩形吗?猜想加证明判定定理:有三个角是直角的四边形是矩形.已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.分析:利用同旁内角互补,两直线平行来证明四边形是平行四边形,可使问题得证.证明:∵ ∠A=∠B=∠C=90°,∴∠A+∠B=180°,∠B+∠C=180°.∴AD∥BC,AB∥CD.求证:四边形ABCD是矩形.∴四边形ABCD是平行四边形.∴四边形ABCD是矩形.练习自我诊断 1、能够判断一个四边形是矩形的条件是( )
A 对角线相等 B 对角线垂直
C对角线互相平分且相等 D对角线垂直且相等
2、矩形的一组邻边长分别是3cm和4cm,则它的对角线长是 cm
3、如图,直线EF∥MN,PQ交EF、MN于A、C两点,AB、CB、CD、AD分别是∠ EAC、 ∠ MCA、 ∠ ACN、 ∠ CAF的角平分线,则四边形ABCD是( )
A 菱形 B 平行四边形
C 矩形 D 不能确定 1、如图,矩形ABCD的对角线AC、BD相交于O,∠BOC=2 ∠ AOB,若AC=6cm,试求AB的长.
2、如图,O是菱形ABCD对角线的交点,作DE∥AC,CE∥BD,DE、CE交于点E,四边形CEDO是矩形吗?说出你的理由.随堂练已知:如图,四边形ABCD是平行四边形,P是CD上的一点,且AP和BP分别分别平分∠DAB和∠CBA,QP∥AD,交AB于点Q.
(1).求证:AP⊥PB;
(2).如果AD=5cm,AP=8cm,那么AB的长是多少? △APB的面积是多少?随堂练
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
