(冀教版九年级上)数学: 32.4 等腰梯形的性质定理和判定定理及其证明(课件)
文档属性
| 名称 | (冀教版九年级上)数学: 32.4 等腰梯形的性质定理和判定定理及其证明(课件) |  | |
| 格式 | rar | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-11-10 13:25:00 | ||
图片预览






文档简介
课件18张PPT。32.4等腰梯形的
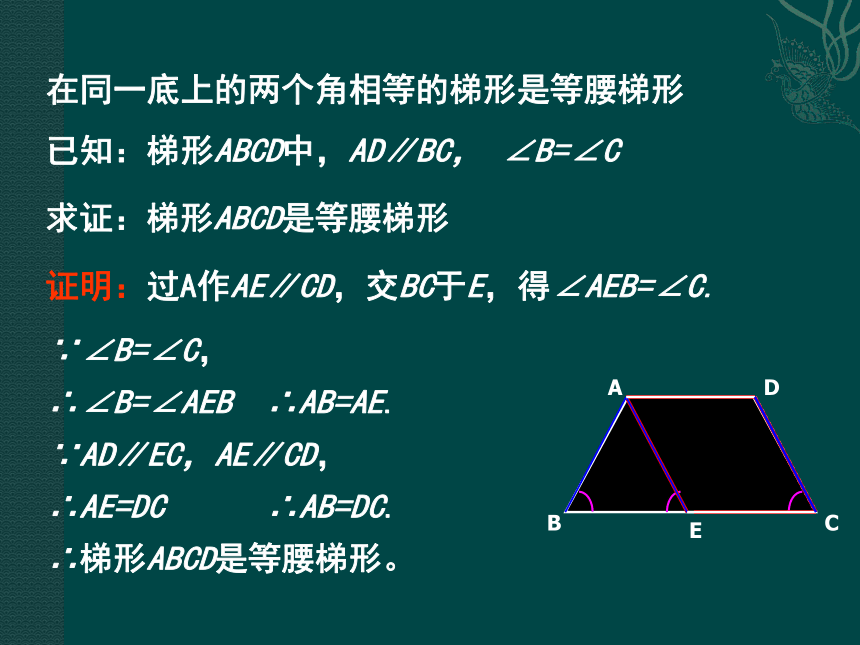
性质定理和判定定理及其证明知识回顾:1、已知四边形ABCD中AB∥CD,AD≠BC,则四边形ABCD是( )形,AB、CD叫( ),AD、BC叫做( )AB与CD间的距离叫做( )。梯梯形的底梯形的腰梯形的高2、在梯形ABCD中, AD∥BC,AB⊥BC于点B,则梯形ABCD叫做( )梯形。直角3、在梯形ABCD中, AB∥CD,AD=BD,则梯形ABCD是( )梯形。等腰 题设逆命题:在同一底上的两个角相等的梯形是等腰梯形。 等腰梯形在同一底上的两个角相等。结 论等腰梯形性质定理: 已知:梯形ABCD中,AD∥BC, ∠B=∠C求证:梯形ABCD是等腰梯形证明:过A作AE∥CD,交BC于E,得∠AEB=∠C.在同一底上的两个角相等的梯形是等腰梯形∵∠B=∠C,
∴∠B=∠AEB ∴AB=AE.
∵AD∥EC,AE∥CD,
∴AE=DC ∴AB=DC.
∴梯形ABCD是等腰梯形。
E 等腰梯形的判定定理: 在同一底上的两个角相
等的梯形是等腰梯形。等腰梯形的两条对角线相等。题 设 逆命题:两条对角线相等的梯形是等腰梯形
结 论等腰梯形性质: 梯 形 —— 梯形的判定例2 求证:两条对角线相等的梯形是等腰梯形已知:在梯形ABCD中,AD∥BC,AC=BD求证:AB=DC分析:EΔ ABC ≌Δ DCB AC= BD,BC=BC12∠ACB=∠DBC用已知AC=BD来构造等腰三角形∠1=∠2=∠X知识拓展:用下面方法证明等腰梯形的判定定理⑴如图,分别延长梯形ABCD的腰BA、CD设它们相交于点E.通过证明Δ EAD 和Δ EBC是等腰三角形,来证明定理AEDCB12已知:在梯形ABCD中,AD∥BC,∠B=∠C求证:AB=CD证明:∵∠B=∠C又∵ AD∥BC∴∠1=∠2∴EB=EC ∴∠1=∠B, ∠2=∠C∴EA=ED∴EB-EA=EC-ED即AB=CDE12已知:在梯形ABCD中,AD∥BC,AC=BD求证:AB=DC证明:过点D作DE∥AC,交BC的延长线于E,得□ ACED,所以DE=AC∵AC=BD,∴DE=BD.∴∠1=∠E,∵∠1=∠2,∴Δ ABC ≌Δ DCB∵∠2=∠E,∴AB=DC又∵AC=BD,BC=CB,⑵如图,作梯形ABCD的高AE、DF.通过证明RtΔABE ≌Δ DCF来证明定理。AFEDCB已知:在梯形ABCD中,AD∥BC,∠B=∠C求证:AB=CD证明:∵ AD∥BC AE⊥BC,DF⊥BC∴AE=DF又∵∠B=∠C∴ RtΔABE ≌ΔDCF∴ AB=CD常用的添加辅助的方法 由等腰梯形的性质定理和判定定理的证明及例2,你能总结一下证明有关等腰梯形的常用方法吗? 证明有关等腰梯形的问题,往往根据问题的需要,恰当地添加辅助线,把它转化为有关等腰三角形或平行四边形的问题。 移动一腰,即从梯形的一个顶点作一腰的平行线,把梯形分成一个平行四边形和一个三角形。 移动一条对角线,即过底的一端作对角线的平等线。可以借助所得到的平行四边形来研究梯形。 从一底的两端作另一底的垂线,把梯形分成一个矩形和两个直角三角形。如果是等腰梯形,所得到的两个直角三角形是全等的。布置作业:课后习题 延长梯形的两交于一点,得到两个三角形。如果是等腰梯形,则得到分别以梯形两底为底的等腰三角形。
性质定理和判定定理及其证明知识回顾:1、已知四边形ABCD中AB∥CD,AD≠BC,则四边形ABCD是( )形,AB、CD叫( ),AD、BC叫做( )AB与CD间的距离叫做( )。梯梯形的底梯形的腰梯形的高2、在梯形ABCD中, AD∥BC,AB⊥BC于点B,则梯形ABCD叫做( )梯形。直角3、在梯形ABCD中, AB∥CD,AD=BD,则梯形ABCD是( )梯形。等腰 题设逆命题:在同一底上的两个角相等的梯形是等腰梯形。 等腰梯形在同一底上的两个角相等。结 论等腰梯形性质定理: 已知:梯形ABCD中,AD∥BC, ∠B=∠C求证:梯形ABCD是等腰梯形证明:过A作AE∥CD,交BC于E,得∠AEB=∠C.在同一底上的两个角相等的梯形是等腰梯形∵∠B=∠C,
∴∠B=∠AEB ∴AB=AE.
∵AD∥EC,AE∥CD,
∴AE=DC ∴AB=DC.
∴梯形ABCD是等腰梯形。
E 等腰梯形的判定定理: 在同一底上的两个角相
等的梯形是等腰梯形。等腰梯形的两条对角线相等。题 设 逆命题:两条对角线相等的梯形是等腰梯形
结 论等腰梯形性质: 梯 形 —— 梯形的判定例2 求证:两条对角线相等的梯形是等腰梯形已知:在梯形ABCD中,AD∥BC,AC=BD求证:AB=DC分析:EΔ ABC ≌Δ DCB AC= BD,BC=BC12∠ACB=∠DBC用已知AC=BD来构造等腰三角形∠1=∠2=∠X知识拓展:用下面方法证明等腰梯形的判定定理⑴如图,分别延长梯形ABCD的腰BA、CD设它们相交于点E.通过证明Δ EAD 和Δ EBC是等腰三角形,来证明定理AEDCB12已知:在梯形ABCD中,AD∥BC,∠B=∠C求证:AB=CD证明:∵∠B=∠C又∵ AD∥BC∴∠1=∠2∴EB=EC ∴∠1=∠B, ∠2=∠C∴EA=ED∴EB-EA=EC-ED即AB=CDE12已知:在梯形ABCD中,AD∥BC,AC=BD求证:AB=DC证明:过点D作DE∥AC,交BC的延长线于E,得□ ACED,所以DE=AC∵AC=BD,∴DE=BD.∴∠1=∠E,∵∠1=∠2,∴Δ ABC ≌Δ DCB∵∠2=∠E,∴AB=DC又∵AC=BD,BC=CB,⑵如图,作梯形ABCD的高AE、DF.通过证明RtΔABE ≌Δ DCF来证明定理。AFEDCB已知:在梯形ABCD中,AD∥BC,∠B=∠C求证:AB=CD证明:∵ AD∥BC AE⊥BC,DF⊥BC∴AE=DF又∵∠B=∠C∴ RtΔABE ≌ΔDCF∴ AB=CD常用的添加辅助的方法 由等腰梯形的性质定理和判定定理的证明及例2,你能总结一下证明有关等腰梯形的常用方法吗? 证明有关等腰梯形的问题,往往根据问题的需要,恰当地添加辅助线,把它转化为有关等腰三角形或平行四边形的问题。 移动一腰,即从梯形的一个顶点作一腰的平行线,把梯形分成一个平行四边形和一个三角形。 移动一条对角线,即过底的一端作对角线的平等线。可以借助所得到的平行四边形来研究梯形。 从一底的两端作另一底的垂线,把梯形分成一个矩形和两个直角三角形。如果是等腰梯形,所得到的两个直角三角形是全等的。布置作业:课后习题 延长梯形的两交于一点,得到两个三角形。如果是等腰梯形,则得到分别以梯形两底为底的等腰三角形。
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
