几种不同类型的函数模型
图片预览





文档简介
课件18张PPT。几类不同增长的函数模型学习目标1.了解指数函数、对数函数、线性函数 (一次函数) 的增长差异.
2.理解对数增长、直线上升、指数爆炸。
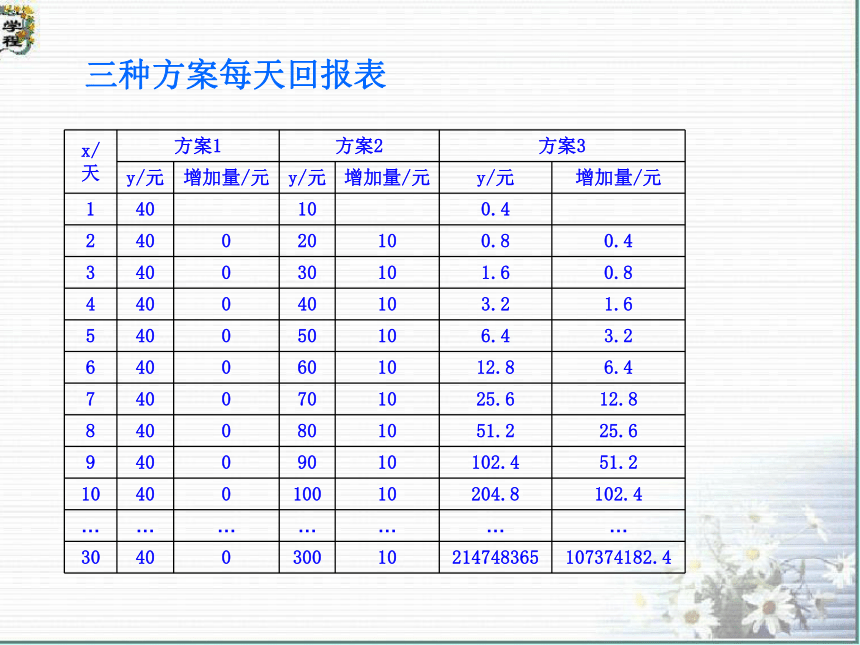
3.了解函数的建模过程。问题情景假如某公司每天向你投资1万元,共投资30天。公司要求你给他的回报是:第一天给公司1分钱,第二天给公司2分钱,以后每天给的钱都是前一天的2倍,共30天,你认为这样的交易对你有利吗?投资天数、回报金额40404040401010+10
=10×210+10+10
=10×310+10+10+10
=10×410+10+10+10+10
=10×50.40.4×20.4×2×2
=0.4×220.4×2×2×2
=0.4×230.4×2×2×2×2
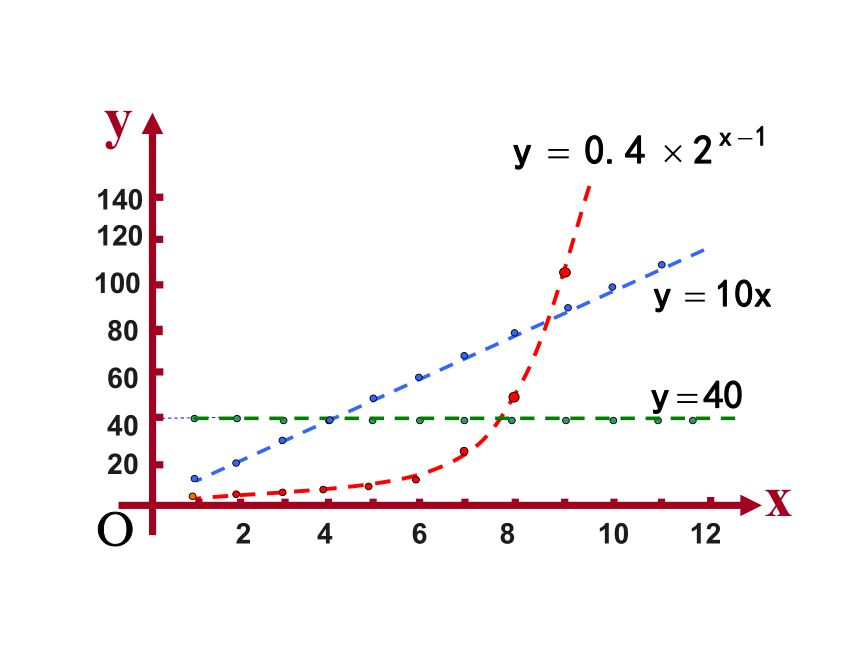
=0.4×24y=40 (x∈N*)y=10x (x∈N*)y=0.4×2x-1 (x∈N*)三种方案每天回报表oxy2040608010012014042681012例1累计回报表投资1~6天,应选择方案一;投资7天,应选择方案一或方案二;投资8~10天,应选择方案二;投资11天(含11天)以上,应选择方案三。情景问题解答假如某公司每天给你投资1万元,共投资30天。公司要求你给他的回报是:第一天给公司1分钱,第二天给公司2分钱,以后每天给的钱都是前一天的2倍,共30天,你认为这样的交易对你有利吗?你30天内给公司的回报为:0.01+0.01×2+0.01×22+…+0.01×229
=10737418.23
≈1074(万元)30万元解答如下:公司30天内为你的总投资为:实际应用问题分析、联想、抽象、转化构建数学模型解答数学问题审 题数学化寻找解题思路还原(设)(列)(解)(答)★ 解答例1的过程实际上就是建立函数模型的过程,
建立函数模型的程序大概如下:一次函数,对数型函数,指数函数。①例2涉及了哪几类函数模型?②你能用数学语言描述符合公司奖励方案的条件吗?例2 某公司为了实现1000万元利润的目标,准备制定
一个激励销售人员的奖励方案:在销售利润达到10万
元时,按销售利润进行奖励,且奖金y (单位:万元)
随销售利润x(单位:万元)的增加而增加,但奖金
总数不超过5万元,同时奖金不超过利润的25%。
现有三个奖励模型:y=0.25x,y=log7x+1,y=1.002x,
其中哪个模型能符合公司的要求?①销售利润达到10万元时,按销售利润进行奖励,且
部门销售利润一般不会超过公司总的利润1000万元,
所以销售利润x可用不等式表示为____________.③依据这个模型进行奖励时,奖金不超过利润的25%,
所以奖金y可用不等式表示为______________.②依据这个模型进行奖励时,奖金总数不超过5万元,
所以奖金y可用不等式表示为__________.10≤x≤10000≤y≤50≤y≤25%x▲ 通过观察图象,你认为哪个模型符合公司的奖励方案?①对于模型y=0.25x,它在区间[10,1000]上递增,
当x>20时,y>5,因此该模型不符合要求;②对于模型y=1.002x,它在区间[10,1000]上递增,
观察图象并结合计算可知,当x>806时,y>5,因此
该模型不符合要求;③对于模型y=log7x+1,它在区间[10,1000]上递增,
观察图象并结合计算可知,当x=1000时,
y=log71000+1≈4.55<5,所以它符合奖金总数不超过
5万元的要求; ★按模型y=log7x+1奖励时,奖金是否不超过利润的25%呢?解:当x∈[10,1000]时,要使y≤0.25x成立,
令f(x)= log7x+1-0.25x,当x∈[10,1000]时,
是否有f(x) ≤0恒成立? 即当x∈[10,1000]时,f(x)= log7x+1-0.25x的
图象是否在x轴下方?
作f(x)= log7x+1-0.25x的图象如下:只需log7x+1≤0.25x成立,即log7x+1-0.25x ≤0。 根据图象观察,f(x)=log7x+1-0.25x的图象在区间[10,1000]内的确在x轴的下方.这说明,按模型y=log7x+1奖励,奖金不会超过利润的25%.课堂小结实际应用问题审 题(设)分析、联想、抽象、转化构建数学模型数学化(列)寻找解题思路(解)解答数学问题还原(答)★课本98页练习2课外作业:
2.理解对数增长、直线上升、指数爆炸。
3.了解函数的建模过程。问题情景假如某公司每天向你投资1万元,共投资30天。公司要求你给他的回报是:第一天给公司1分钱,第二天给公司2分钱,以后每天给的钱都是前一天的2倍,共30天,你认为这样的交易对你有利吗?投资天数、回报金额40404040401010+10
=10×210+10+10
=10×310+10+10+10
=10×410+10+10+10+10
=10×50.40.4×20.4×2×2
=0.4×220.4×2×2×2
=0.4×230.4×2×2×2×2
=0.4×24y=40 (x∈N*)y=10x (x∈N*)y=0.4×2x-1 (x∈N*)三种方案每天回报表oxy2040608010012014042681012例1累计回报表投资1~6天,应选择方案一;投资7天,应选择方案一或方案二;投资8~10天,应选择方案二;投资11天(含11天)以上,应选择方案三。情景问题解答假如某公司每天给你投资1万元,共投资30天。公司要求你给他的回报是:第一天给公司1分钱,第二天给公司2分钱,以后每天给的钱都是前一天的2倍,共30天,你认为这样的交易对你有利吗?你30天内给公司的回报为:0.01+0.01×2+0.01×22+…+0.01×229
=10737418.23
≈1074(万元)30万元解答如下:公司30天内为你的总投资为:实际应用问题分析、联想、抽象、转化构建数学模型解答数学问题审 题数学化寻找解题思路还原(设)(列)(解)(答)★ 解答例1的过程实际上就是建立函数模型的过程,
建立函数模型的程序大概如下:一次函数,对数型函数,指数函数。①例2涉及了哪几类函数模型?②你能用数学语言描述符合公司奖励方案的条件吗?例2 某公司为了实现1000万元利润的目标,准备制定
一个激励销售人员的奖励方案:在销售利润达到10万
元时,按销售利润进行奖励,且奖金y (单位:万元)
随销售利润x(单位:万元)的增加而增加,但奖金
总数不超过5万元,同时奖金不超过利润的25%。
现有三个奖励模型:y=0.25x,y=log7x+1,y=1.002x,
其中哪个模型能符合公司的要求?①销售利润达到10万元时,按销售利润进行奖励,且
部门销售利润一般不会超过公司总的利润1000万元,
所以销售利润x可用不等式表示为____________.③依据这个模型进行奖励时,奖金不超过利润的25%,
所以奖金y可用不等式表示为______________.②依据这个模型进行奖励时,奖金总数不超过5万元,
所以奖金y可用不等式表示为__________.10≤x≤10000≤y≤50≤y≤25%x▲ 通过观察图象,你认为哪个模型符合公司的奖励方案?①对于模型y=0.25x,它在区间[10,1000]上递增,
当x>20时,y>5,因此该模型不符合要求;②对于模型y=1.002x,它在区间[10,1000]上递增,
观察图象并结合计算可知,当x>806时,y>5,因此
该模型不符合要求;③对于模型y=log7x+1,它在区间[10,1000]上递增,
观察图象并结合计算可知,当x=1000时,
y=log71000+1≈4.55<5,所以它符合奖金总数不超过
5万元的要求; ★按模型y=log7x+1奖励时,奖金是否不超过利润的25%呢?解:当x∈[10,1000]时,要使y≤0.25x成立,
令f(x)= log7x+1-0.25x,当x∈[10,1000]时,
是否有f(x) ≤0恒成立? 即当x∈[10,1000]时,f(x)= log7x+1-0.25x的
图象是否在x轴下方?
作f(x)= log7x+1-0.25x的图象如下:只需log7x+1≤0.25x成立,即log7x+1-0.25x ≤0。 根据图象观察,f(x)=log7x+1-0.25x的图象在区间[10,1000]内的确在x轴的下方.这说明,按模型y=log7x+1奖励,奖金不会超过利润的25%.课堂小结实际应用问题审 题(设)分析、联想、抽象、转化构建数学模型数学化(列)寻找解题思路(解)解答数学问题还原(答)★课本98页练习2课外作业:
