1.3实数

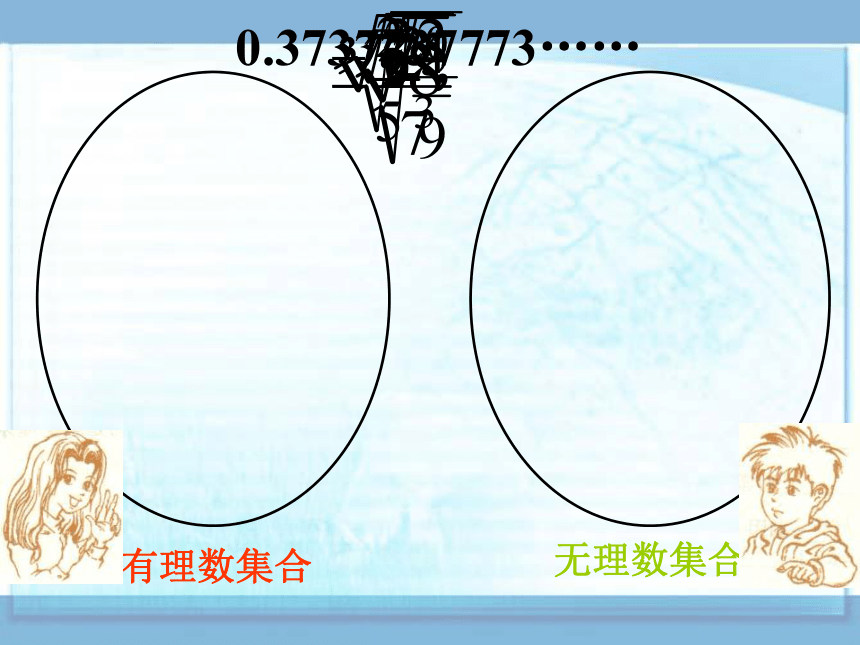
课件18张PPT。1.3 实 数0.3737737773……把下列各数分别填入相应的集合内：有理数集合无理数集合0.3737737773……0 有理数和无理数统称为实数(real number) 所有实数组成的集合叫作实数集无理数
(无限不循环小数)实数自然数分数非负数(有理数)负数(有理数)有理数
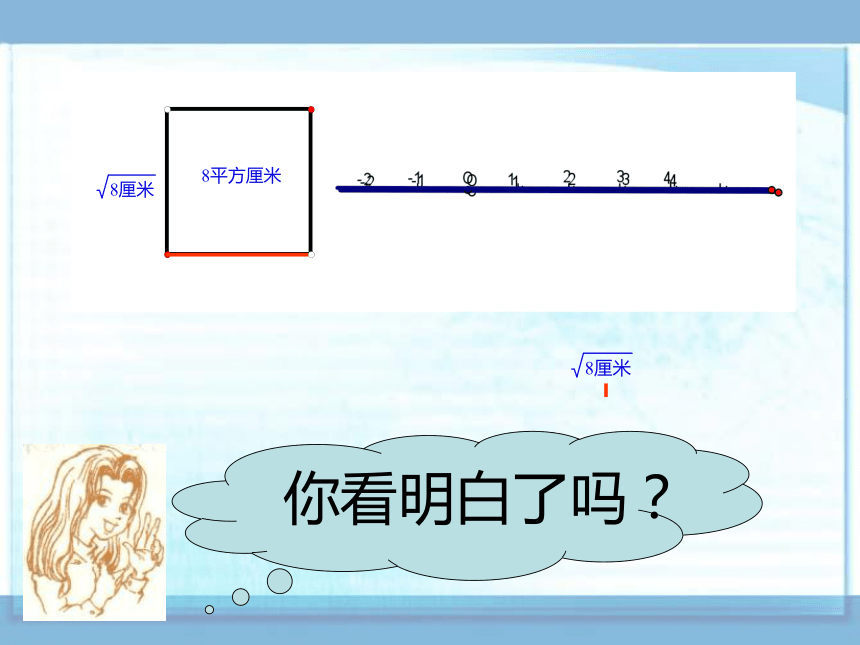
(有限小数或无限循环小数)正整数零我们学习数的经历: 同学们已经知道，每一个有理数都可以用数轴上唯一的一个点来表示.试问：每一个无理数是不是也可以用数轴上唯一的一个点来表示呢？实数与数轴:同学们要善于开发自己创新能力.你看明白了吗？这可以说明：每一个实数都可以用数轴上唯一的一个点来表示.我们还可以说明：数轴上每一个点都表示唯一的一个实数.上面两个结论结合起来可以简洁地说成：实数和数轴上的点一一对应实数分为正实数、零、负实数 如果在数轴上表示，正实数、零、负实数应该在数轴的原点的哪侧呢？正实数负实数零 与有理数的情形类似，如果两个实数只有符号不同，那么其中的一个数叫作另一个的相反数，也说它们互为相反数. 在数轴上，表示一个数的点与原点的距离叫作这个实数的绝对值.知识回顾：
1、有理数的运算法则有哪些？2、有理数的运算律有哪些？ 实数和有理数一样也可以进行加、减、乘、除、乘方运算，而且有理数的运算法则与运算律对实数仍然适用.例如：乘法交换律乘法结合律合并同类项法则练习：求下列各数的相反数、倒数和绝对值：22-77结合课本，熟悉并且掌握有效数字，近似值等名词的含义.
掌握有效数字的取位原则和方法. 和 统称为实数.
- 绝对值是 ,相反数是 ,倒数是 .
数轴上的点与 具有 对应关系.
化简: = ; = ; = ; = .
下列说法（1）带根号的数是无理数；（2）无限小数都是无理数；（3）无理数都是无限小数；（4）在实数范围内，一个数不是有理数，则一定是无理数，不是正数，则一定是负数。其中错误的有 个。
把下列各数填在相应的集合里：
， ，- ，-65， ， ，- ， ，1.3232232223…
有理数集合:( )
无理数集合:( )
正数集合:( )
负数集合:( )基础训练:1、下列说法中错误的一个是（ ）
A、如果a、b 互为相反数，那么a+1和b-1仍是相反数；
B、不论x是什么实数，x -2x+ 的值 总是大于0；
C、如果 是一个无理数，那么a是非完全平方数。
2、1.7- 的相反数是 ,1.7- 的绝对值等于 .
3、设a、b是有理数，且满足a+ b=（1- ），求a 的值。
能力训练： 《有理数和无理数之战》 　　 在一个早晨，同学小毅一觉醒来，发现窗户外的山坡上在打仗.仔细一看，一边打着“有理数”的大旗子，一边打着“无理数”的大旗子.　　有理数和无理数为什么要打仗？哦，原来是为了名字.　　听听无理数司令π怎么说：“我们无理数和有理数同样是数，为什么他们‘有理’，我们‘无理’？我们究竟哪点儿无理？”　　对呀！无理怎么会存在嘛！小毅心里也在琢磨. “因为人们最开始发现的是有理数，见到我们无理数时还不理解，所以取了‘无理数’这么难听的名字.可是现在，人们已经充分认识我们了，就该给我们摘掉‘无理’的帽子才对！” 小结：“无理数”和“有理数”仅是名称而已，据说是清朝末年从日本引进时，翻译的讹误，因此不能从词义上理解，它们根本的区别，就是凡是有理数，都可以化成两个整数之比（可看成一个分数），而无理数，无论如何也不能化成两个整数之比（不能化为分数）.