4.2正切1

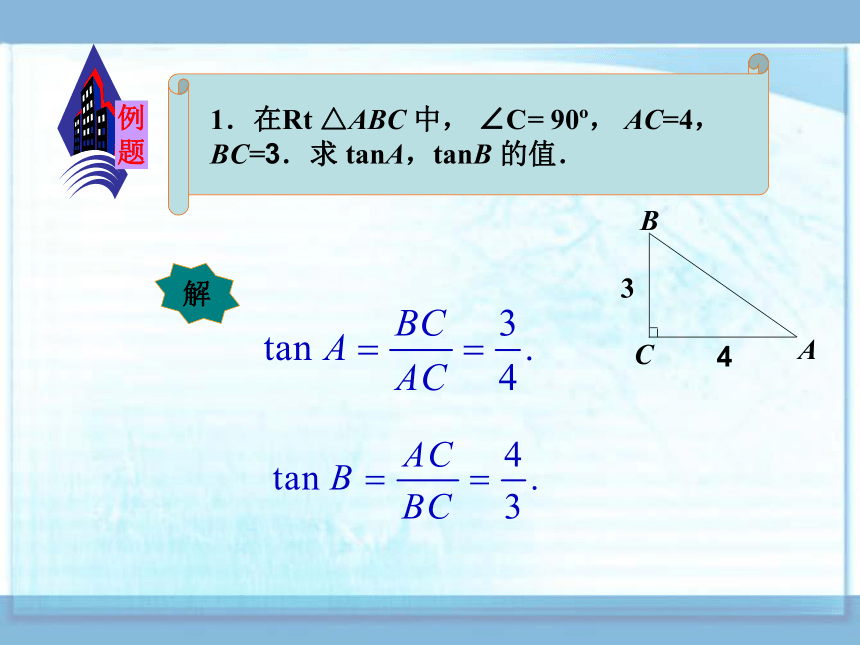
课件9张PPT。4.2　正切（1）观察在离铁塔130m的A处，用仪器测得塔顶的仰角为25o，仪器的高为1.4m，你能求出铁塔的高BD吗？AE=1.4m，AC=130m ，只要求出△ABC的边长BC，塔高等于BC加上AE即可.类似地可以证明：在有一个锐角等于α的所有直角三角形中，角α的对边与斜边的比值为一个常数．在Rt △ABC 中， ∠A=25o， AC=130m， ∠A的对边为 BＣ．邻边为AC，因而铁塔的高在直角三角形中，锐角α的对边与邻边的比叫作角α的正切，记作　tanα．tanα现在求铁塔的高．例 题例 题在Rt △ABC 中， ∠C= 90o， ∠A= 30o， 于是从而因此由于∠B= 60o因此说一说　30o　45o　60o　的正弦、余弦、正切值．做一做1．用计算器求锐角的正切值（精确到0.0001）：　2．已知正切值，用计算器求相应的锐角 （精确到1′）．（１）tan21o 15′≈（２）tan89o 27′≈（３）tan5o 49′≈0.3889104.17090.1019（1）tanα＝1.2868，　则α ≈（2）tanα =108.5729，则α ≈52o 9′89o 28′练 习1．在Rt △ABC 中， ∠C= 90o， AC=7，BC=5．求 tanA ，tanB的值．2．在Rt △ABC 中， ∠C= 90o，AC=2，AB=3．求 tanA ，tanB 的值． 　　答案：答案：3．求下列各式的值：（1）（2）（ 　 4 　）（　　　　）小结本节主要讲述：　　在直角三角形中，利用正切公式求直角边的长及一些特殊角的正切值；以及利用正切公式解决实际问题．