4.3解直角三角形及其应用2

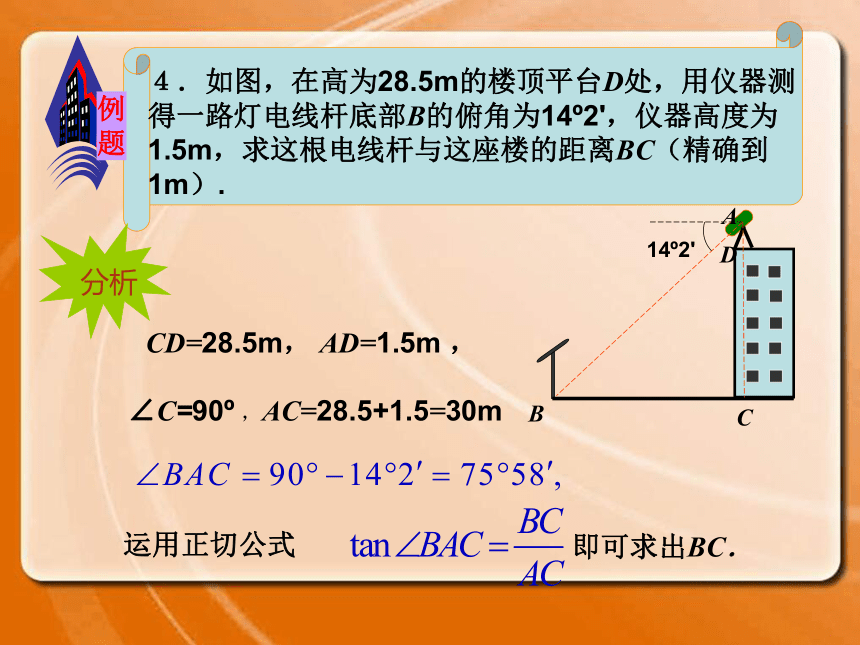
课件8张PPT。4.3　解直角三角形及其应用（2）例 题３．如图，一艘游船在离开码头A后，以和河岸成20o角的方向行驶了500m到达B处，求B处与河岸的距离（精确到1m）．BC⊥CA ，∠A=20oAB=500mBC是∠A的对边，AB是斜边，根据正弦公式，就可求出BC．从点B向河岸作垂线，垂足为C，在 Rt△ABC 中，∠C= 90o， ∠A =20o，AB=500m,由于BC是∠A的对边，AB是斜边CB答：B处与河岸的距离约为171m．例 题CD=28.5m， AD=1.5m ，∠C=90o ，AC=28.5+1.5=30m运用正切公式即可求出BC．在 Rt△ABC 中，∠C= 90o， ∠BAC =75o58'，AC=30m,由于BC是∠BAC的对边，AC是邻边，答：这根电线杆与这座楼的距离约为120 m．由题意，△ABC是直角三角形， 其中∠C =90o，∠A= 71o34'，∠A所对的边BC=2400m，求 AC=？ 一艘帆船航行到 B处时，灯塔A在船的北偏东71o34'的方向，帆船从B处继续向正东方向航行2400m到达C处，此时灯塔A在船的正北方向．求C处和灯塔A的距离（精确到1m）.练 习即可．在 Rt△ABC 中，∠C= 90o， ∠A =71o34'，BC=2400m,由于BC是∠A的对边，AC是邻边，答：C处与灯塔A的距离约为120 m．利用直角三角形中边与角的关系，解决实际问题，难点是分清角的对边．邻边，正确理解锐角的正弦．余弦．正切的概念．１．在 Rt△ABC 中，∠C= 90o， ∠A =28o32‘，C=7.92cm,求∠B（精确到1’），a，b（精确到0.01cm）．２．在 Rt△ABC 中，∠C= 90o， ∠B = 28o32' ，a=　12.36cm,求∠A（精确到1’），c，b（精确到0.01cm）．做一做小结