新课标A版必修1函数的单调性

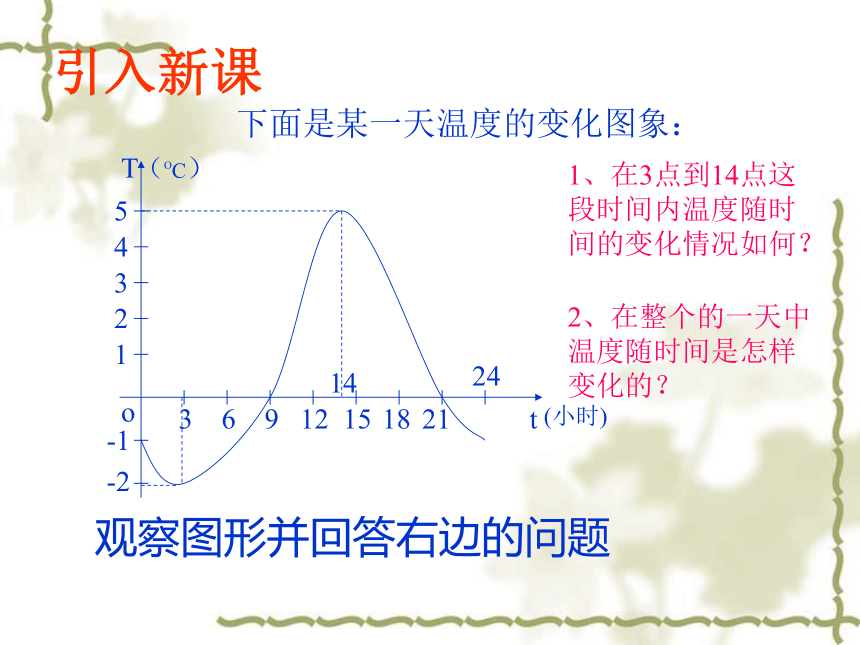
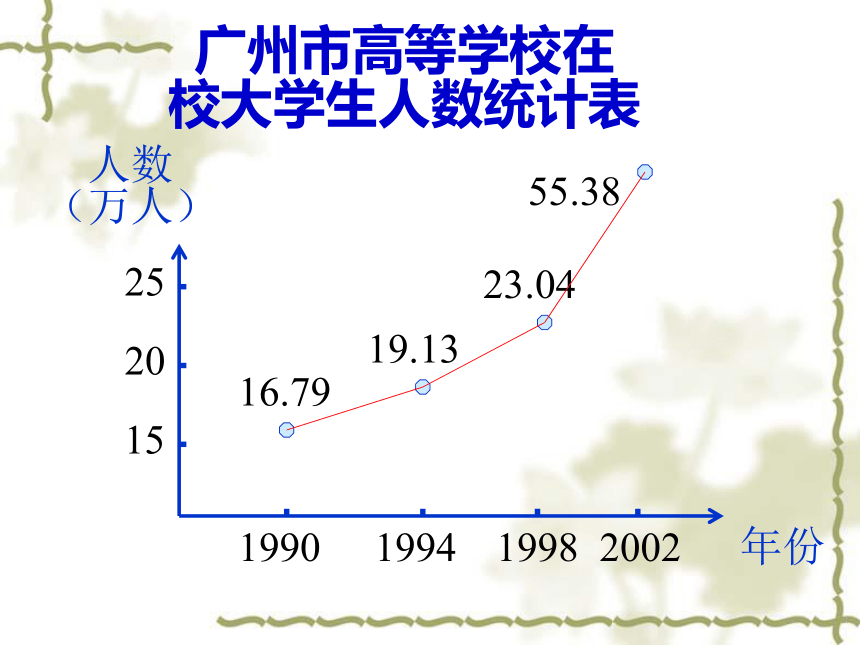
课件26张PPT。函数的基本性质——函数的单调性观察图形并回答右边的问题下面是某一天温度的变化图象：1、在3点到14点这段时间内温度随时间的变化情况如何？2、在整个的一天中温度随时间是怎样变化的？引入新课 广州市高等学校在
校大学生人数统计表年份 人数
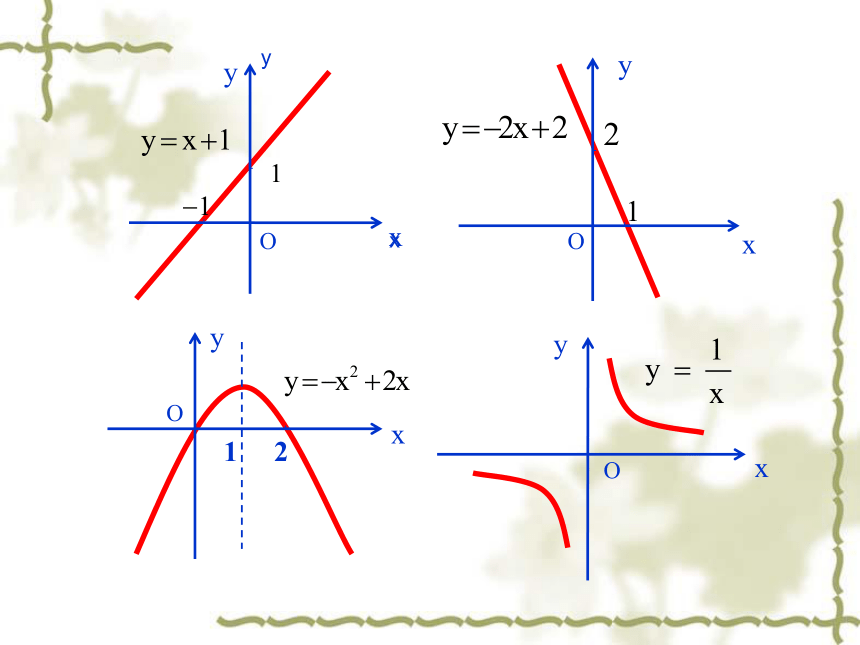
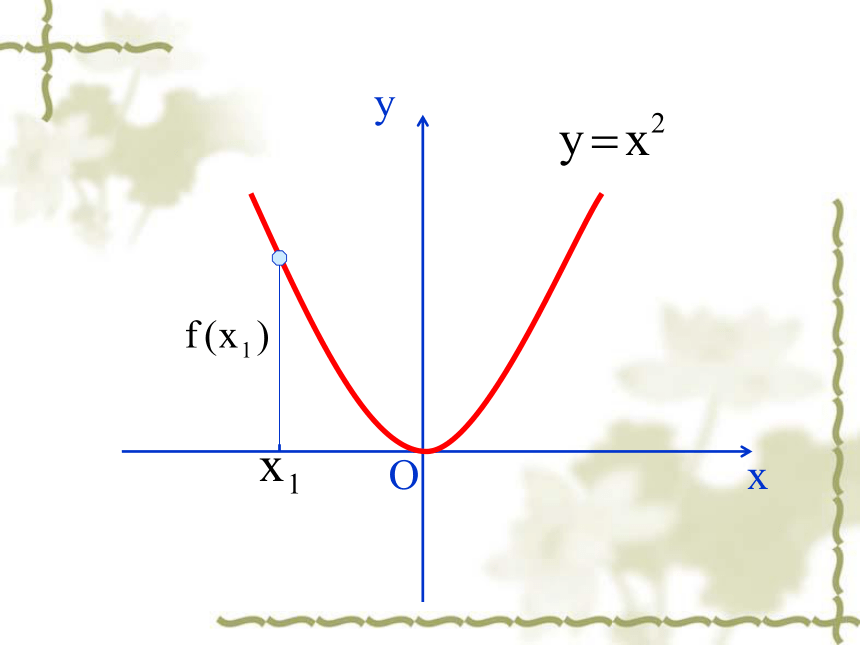
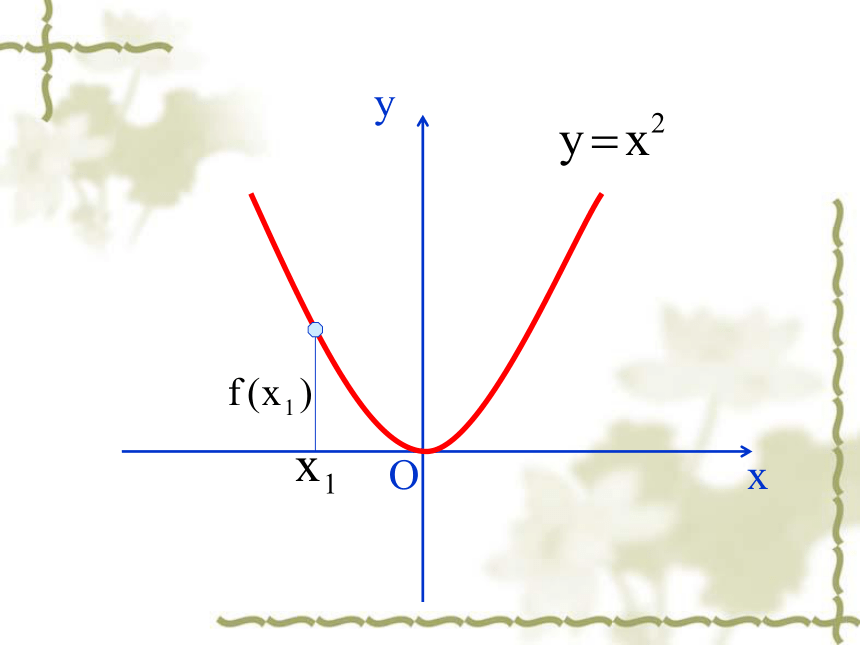
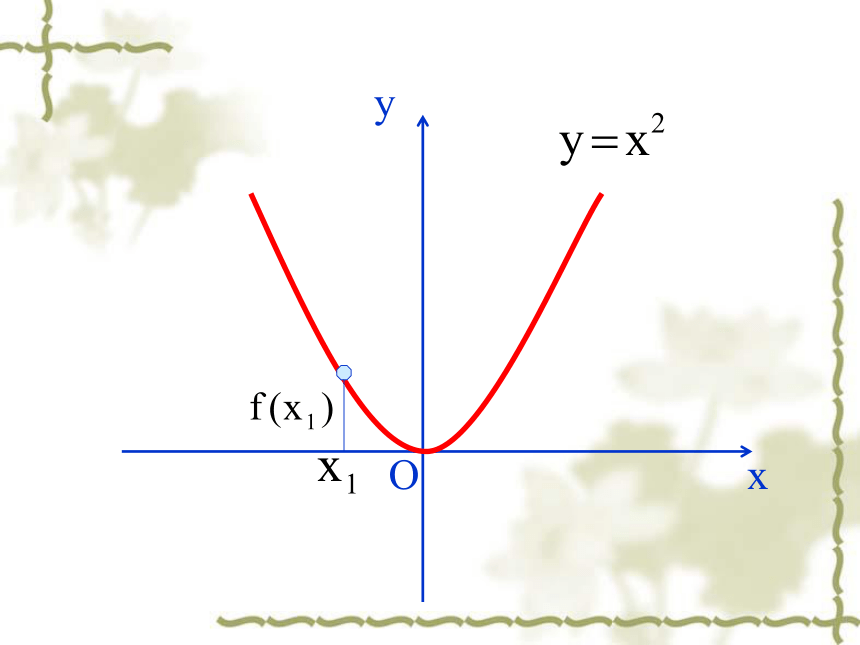
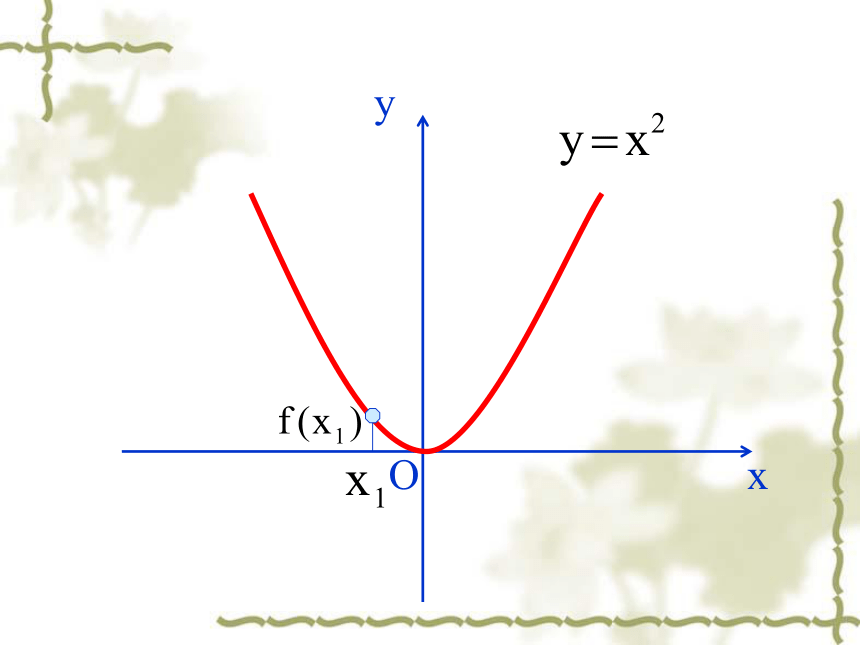
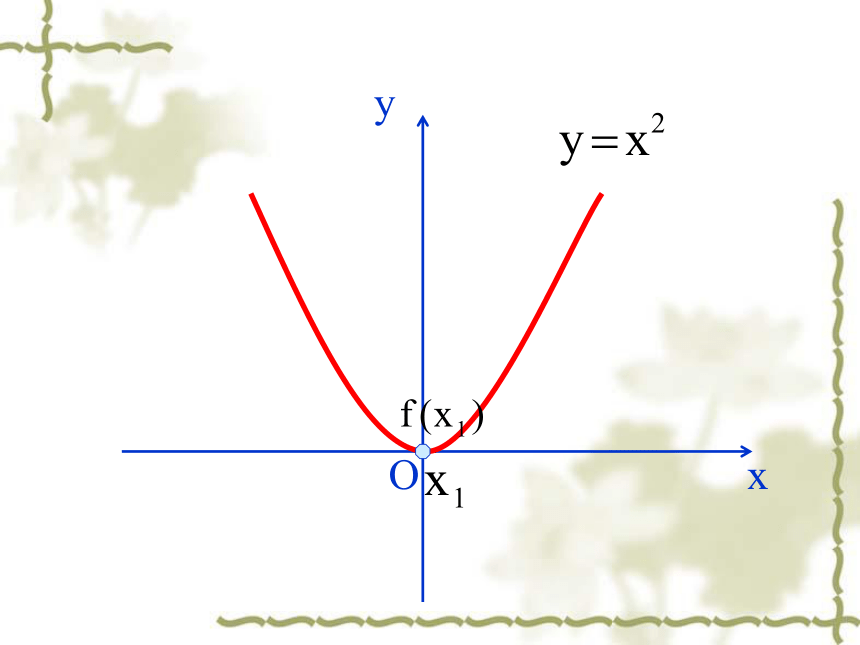
（万人）xOxyOxyOxyOxyOxyOxyOxyOxyOxy 函数f (x)在给定区间上为增函数。如何用x与 f(x)来描述上升的图象？如何用x与 f(x)来描述下降的图象？ 函数f (x)在给定区间上为减函数。 函数的单调性定义:一般地，设函数f(x)的定义域为I 如果对于属于定义域内某个区间上的任意两个自变量的值都有减函数注1 某个区间 2 任意…都有返回这一区间叫函数的单调区间图像特征：在单调区间上增函数的图像是上升的。在单调区间上减函数的图像是下降的。若函数 在某个区间上是增函数或减函数，那么就说函数 在这个区间具有单调性。有对吗？例如 在∴ 得 在 上是增函数， 例1. 如图是定义在闭区间 上的函数 的图像，根据图像说出 的 单调区间，以及在每一单调区间上， 是 增函数还是减函数。 解：函数 单调区间有 ， ， ， ； 其中 在区间 ， 上是减函数；其中 在区间 ， 上是增函数。xy如图,已知函数y=g(x)的图象,根据图象(包括端点)说出函数的单调区间,以及在每一个单调区间上,函数是增函数还是减函数.例2.证明函数 在 上是增函数。于是 即所以 在
上是增函数.证明步骤：论证步骤1）作差2）变形3）判断大小3. 根据定义得到结论。⑴ 配方 ⑵因式分解⑶ 通分1. 设 是某一区间上的任意两个量,且 例3 证明函数
在 R 上是 增函数 . 【讨论】：
1、判断函数f(x)=1/x在(－∞，0)上是增函数还是减函数？如何证明你的结论？
【想一想】：能否说函数f(x)=1/x在(－∞，+∞)
上是减函数？
答：不能. 因为x=0不属于f(x)=1/x的定义域.
减函数 2、判断函数f(x)=1/x在(0，+∞)上
是增函数还是减函数？如何证明你的结论？
减函数[例4]证明函数 在(0,+∞)上是减函数. 证明:设任意x1,x2∈(0,+∞),且x10 又x10 ∴f（x1）-f（x2）>0 即f（x1）>f（x2） ∴ 在(0,+∞)上是减函数. yxo不满足减函数的定义不是减函数.课堂小结：（1）函数单调性的 ； （2）研究函数单调性的常用方法:作业方法一：分析函数值大小的变化;方法二：分析函数的图象;方法三：利用函数单调性的定义.
定义