(北京课改版九年级上)数学:19.5 相似三角形的判定(课件)
文档属性
| 名称 | (北京课改版九年级上)数学:19.5 相似三角形的判定(课件) |

|
|
| 格式 | rar | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 京教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-11-12 00:00:00 | ||
图片预览











文档简介
课件36张PPT。 相似三角形的判定(一)判定两个三角形相似的方法: 平行 相似复 习(1)定义(2)相似三角形判定的预备定理判定三角形全等有哪些方法?类比三角形全等的判定方法,相似三角形的判定方法有哪些?全等三角形
的判定方法 相似三角形
的判定方法全等三角形
的判定方法
定义
边角边公理
角边角公理
角角边定理
边边边公理
斜边、直角
边公理 相似三角形
的判定方法定义
定理
如图,在△ABC和△A′B ′C ′中,
∠A=∠A′ ,∠B=∠B′ .
△ABC与△A′B′C′ 是否相似?.
已知:如图,在△ABC和△A′B′C ′
中,∠A=∠A′ ,∠B=∠B′ .
求证:△ABC∽△A′B′C′.
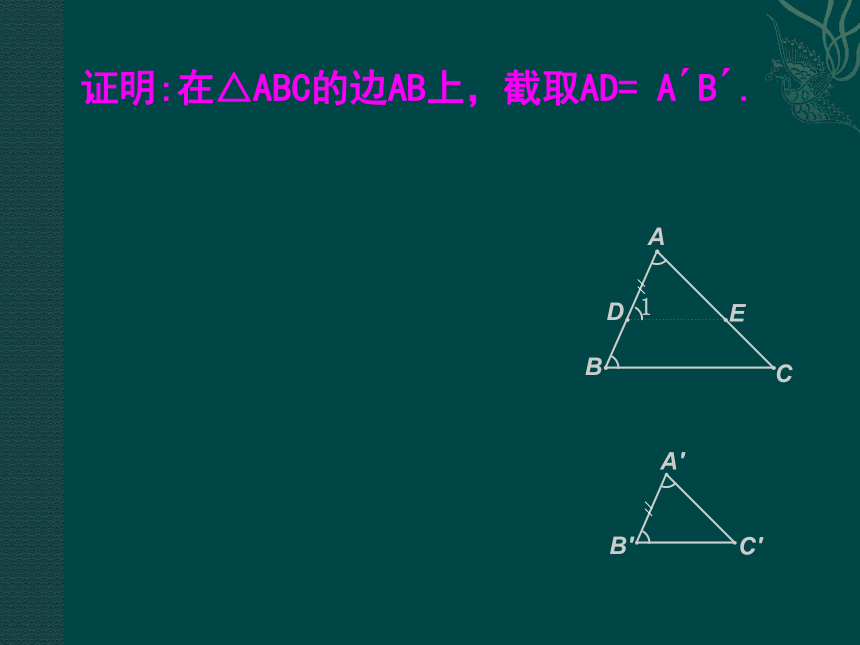
证明:在△ABC的边AB上,截取AD= A′B′.证明:在△ABC的边AB上,截取AD= A′B′.
过点D作DE∥BC,交AC于点E,
则有△ADE∽△ABC.
证明:在△ABC的边AB上,截取AD= A′B′.
过点D作DE∥BC,交AC于点E,
则有△ADE∽△ABC.
∵∠1=∠B,∠B=∠B′,
证明:在△ABC的边AB上,截取AD= A′B′.
过点D作DE∥BC,交AC于点E,
则有△ADE∽△ABC.
∵∠1=∠B,∠B=∠B′,
∴∠1=∠B′ .
证明:在△ABC的边AB上,截取AD= A′B′.
过点D作DE∥BC,交AC于点E,
则有△ADE∽△ABC.
∵∠1=∠B,∠B=∠B′,
∴∠1=∠B′ .
又∠A=∠A′,AD=A′B′,
证明:在△ABC的边AB上,截取AD= A′B′.
过点D作DE∥BC,交AC于点E,
则有△ADE∽△ABC.
∵∠1=∠B,∠B=∠B′,
∴∠1=∠B′ .
又∠A=∠A′,AD=A′B′,
∴△ADE≌△A′B′C′.证明:在△ABC的边AB上,截取AD= A′B′.
过点D作DE∥BC,交AC于点E,
则有△ADE∽△ABC.
∵∠1=∠B,∠B=∠B′,
∴∠1=∠B′ .
又∠A=∠A′,AD=A′B′,
∴△ADE≌△A′B′C′.
∴△ABC∽△A′B′C′.
如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
两角对应相等,两三角形相似.
判 定 定 理 1 用推理的形式来表达:
在△ABC 和△A′B′C′中,
∵∠A=∠A′,∠B=∠B′,
∴△ABC ∽△A′B′C′.
(两角对应相等,两三角形相似)例1 已知:△ABC和△DEF中,∠A=40°,
∠B=80°,∠E=80°,∠F=60°.
求证:△ABC∽△DEF.
例1 已知:△ABC和△DEF中,∠A=40°,
∠B=80°,∠E=80°,∠F=60°.
求证:△ABC∽△DEF.
40 °例1 已知:△ABC和△DEF中,∠A=40°,
∠B=80°,∠E=80°,∠F=60°.
求证:△ABC∽△DEF.
40 °80 °例1 已知:△ABC和△DEF中,∠A=40°,
∠B=80°,∠E=80°,∠F=60°.
求证:△ABC∽△DEF.
80 °40 °80 °例1 已知:△ABC和△DEF中,∠A=40°,
∠B=80°,∠E=80°,∠F=60°.
求证:△ABC∽△DEF.
80 °60 °40 °80 °例1 已知:△ABC和△DEF中,∠A=40°,
∠B=80°,∠E=80°,∠F=60°.
求证:△ABC∽△DEF.
60°∴△ABC∽△DEF(两角对应相等,两三角形相似).证明:∵在△ABC中,∠A=40°,∠B=80°,∴∠C=60°.
∵在△DEF中,∠E=80°,∠F=60°,∴∠B =∠E,∠C =∠F.判断正误,并说明理由:任意等边三角形是相似三角形;
有一角对应相等的两等腰三角形是相似三角形;
顶角对应相等的两等腰三角形是相似三角形;
任意直角三角形都相似;
有一锐角对应相等的两直角三角形相似。 在Rt△ABC中,CD是斜边上的高,角形,并说明理由.Rt△ABC∽Rt△ACD∽Rt△CBD.证明:∵在△ABC中,∠ACB=90°,
CD⊥AB于D,ABCD证明:∵在△ABC中,∠ACB=90°,
CD⊥AB于D,
∴∠CDB=∠ACB=90°.ABCD证明:∵在△ABC中,∠ACB=90°,
CD⊥AB于D,
∴∠CDB=∠ACB=90°.
∵∠B=∠B,
ABCD证明:∵在△ABC中,∠ACB=90°,
CD⊥AB于D,
∴∠CDB=∠ACB=90°,
∵∠B=∠B,
∴△ABC∽△CBD(两角对应相等,两
三角形相似).ABCD证明:∵在△ABC中,∠ACB=90°,
CD⊥AB于D,
∴∠CDB=∠ACB=90°,
∵∠B=∠B,
∴△ABC∽△CBD(两角对应相等,两
三角形相似).
同理△ABC∽△ACD.
ABCD证明:∵在△ABC中,∠ACB=90°,
CD⊥AB于D.
∴∠CDB=∠ACB=90°,
∵∠B=∠B,
∴△ABC∽△CBD(两角对应相等,两
三角形相似).
同理△ABC∽△ACD.
∴△ABC∽△CBD∽△ACD.
ABCD画一画 已知:∠A=60°,∠B=75°,请你画一个△DEF与△ABC相似.
DEDEM60°DEMN60°75°DEMNF60°75°小 结(1)判定三角形相似的判定方法:定义、预备定理、定理1(2)基本图形:(3)学习方法:类比旧知识学习新知识
的判定方法 相似三角形
的判定方法全等三角形
的判定方法
定义
边角边公理
角边角公理
角角边定理
边边边公理
斜边、直角
边公理 相似三角形
的判定方法定义
定理
如图,在△ABC和△A′B ′C ′中,
∠A=∠A′ ,∠B=∠B′ .
△ABC与△A′B′C′ 是否相似?.
已知:如图,在△ABC和△A′B′C ′
中,∠A=∠A′ ,∠B=∠B′ .
求证:△ABC∽△A′B′C′.
证明:在△ABC的边AB上,截取AD= A′B′.证明:在△ABC的边AB上,截取AD= A′B′.
过点D作DE∥BC,交AC于点E,
则有△ADE∽△ABC.
证明:在△ABC的边AB上,截取AD= A′B′.
过点D作DE∥BC,交AC于点E,
则有△ADE∽△ABC.
∵∠1=∠B,∠B=∠B′,
证明:在△ABC的边AB上,截取AD= A′B′.
过点D作DE∥BC,交AC于点E,
则有△ADE∽△ABC.
∵∠1=∠B,∠B=∠B′,
∴∠1=∠B′ .
证明:在△ABC的边AB上,截取AD= A′B′.
过点D作DE∥BC,交AC于点E,
则有△ADE∽△ABC.
∵∠1=∠B,∠B=∠B′,
∴∠1=∠B′ .
又∠A=∠A′,AD=A′B′,
证明:在△ABC的边AB上,截取AD= A′B′.
过点D作DE∥BC,交AC于点E,
则有△ADE∽△ABC.
∵∠1=∠B,∠B=∠B′,
∴∠1=∠B′ .
又∠A=∠A′,AD=A′B′,
∴△ADE≌△A′B′C′.证明:在△ABC的边AB上,截取AD= A′B′.
过点D作DE∥BC,交AC于点E,
则有△ADE∽△ABC.
∵∠1=∠B,∠B=∠B′,
∴∠1=∠B′ .
又∠A=∠A′,AD=A′B′,
∴△ADE≌△A′B′C′.
∴△ABC∽△A′B′C′.
如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
两角对应相等,两三角形相似.
判 定 定 理 1 用推理的形式来表达:
在△ABC 和△A′B′C′中,
∵∠A=∠A′,∠B=∠B′,
∴△ABC ∽△A′B′C′.
(两角对应相等,两三角形相似)例1 已知:△ABC和△DEF中,∠A=40°,
∠B=80°,∠E=80°,∠F=60°.
求证:△ABC∽△DEF.
例1 已知:△ABC和△DEF中,∠A=40°,
∠B=80°,∠E=80°,∠F=60°.
求证:△ABC∽△DEF.
40 °例1 已知:△ABC和△DEF中,∠A=40°,
∠B=80°,∠E=80°,∠F=60°.
求证:△ABC∽△DEF.
40 °80 °例1 已知:△ABC和△DEF中,∠A=40°,
∠B=80°,∠E=80°,∠F=60°.
求证:△ABC∽△DEF.
80 °40 °80 °例1 已知:△ABC和△DEF中,∠A=40°,
∠B=80°,∠E=80°,∠F=60°.
求证:△ABC∽△DEF.
80 °60 °40 °80 °例1 已知:△ABC和△DEF中,∠A=40°,
∠B=80°,∠E=80°,∠F=60°.
求证:△ABC∽△DEF.
60°∴△ABC∽△DEF(两角对应相等,两三角形相似).证明:∵在△ABC中,∠A=40°,∠B=80°,∴∠C=60°.
∵在△DEF中,∠E=80°,∠F=60°,∴∠B =∠E,∠C =∠F.判断正误,并说明理由:任意等边三角形是相似三角形;
有一角对应相等的两等腰三角形是相似三角形;
顶角对应相等的两等腰三角形是相似三角形;
任意直角三角形都相似;
有一锐角对应相等的两直角三角形相似。 在Rt△ABC中,CD是斜边上的高,角形,并说明理由.Rt△ABC∽Rt△ACD∽Rt△CBD.证明:∵在△ABC中,∠ACB=90°,
CD⊥AB于D,ABCD证明:∵在△ABC中,∠ACB=90°,
CD⊥AB于D,
∴∠CDB=∠ACB=90°.ABCD证明:∵在△ABC中,∠ACB=90°,
CD⊥AB于D,
∴∠CDB=∠ACB=90°.
∵∠B=∠B,
ABCD证明:∵在△ABC中,∠ACB=90°,
CD⊥AB于D,
∴∠CDB=∠ACB=90°,
∵∠B=∠B,
∴△ABC∽△CBD(两角对应相等,两
三角形相似).ABCD证明:∵在△ABC中,∠ACB=90°,
CD⊥AB于D,
∴∠CDB=∠ACB=90°,
∵∠B=∠B,
∴△ABC∽△CBD(两角对应相等,两
三角形相似).
同理△ABC∽△ACD.
ABCD证明:∵在△ABC中,∠ACB=90°,
CD⊥AB于D.
∴∠CDB=∠ACB=90°,
∵∠B=∠B,
∴△ABC∽△CBD(两角对应相等,两
三角形相似).
同理△ABC∽△ACD.
∴△ABC∽△CBD∽△ACD.
ABCD画一画 已知:∠A=60°,∠B=75°,请你画一个△DEF与△ABC相似.
DEDEM60°DEMN60°75°DEMNF60°75°小 结(1)判定三角形相似的判定方法:定义、预备定理、定理1(2)基本图形:(3)学习方法:类比旧知识学习新知识
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
