(北京课改版九年级上)数学:19.7 相似三角形的应用举例 课件
文档属性
| 名称 | (北京课改版九年级上)数学:19.7 相似三角形的应用举例 课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 京教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-11-12 00:00:00 | ||
图片预览


文档简介
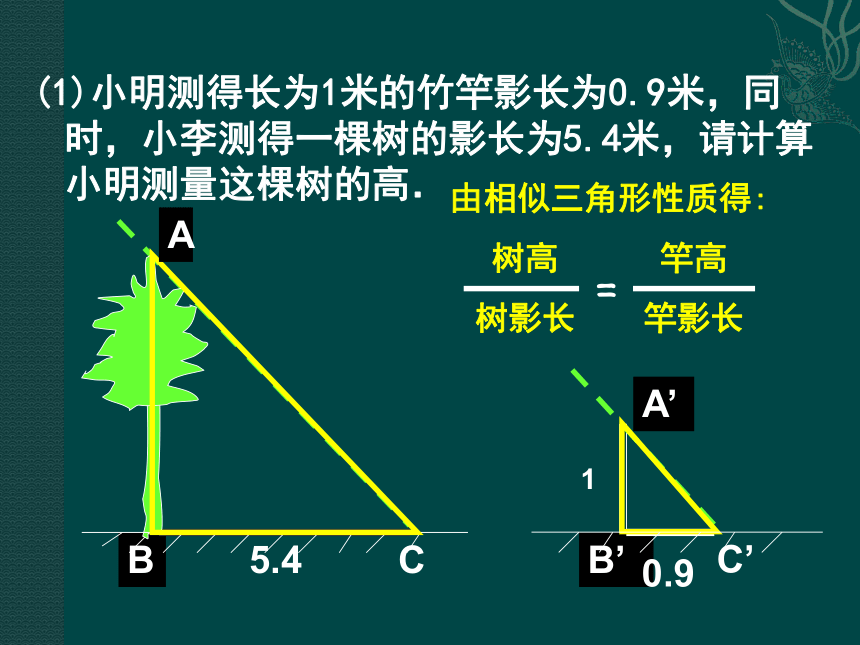
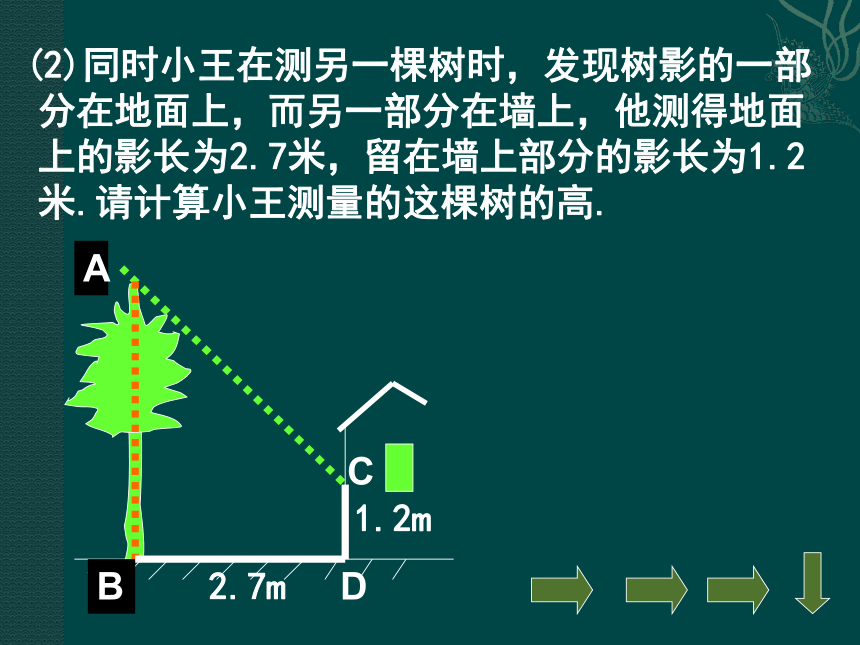
课件16张PPT。 相似三角形的应用(一)议一议:教学楼前边有一排树,学习了相似三角形后,数学兴趣小组的同学们想利用树影测量树高. 你知道他们是怎样测量的吗?BB’(1)小明测得长为1米的竹竿影长为0.9米,同时,小李测得一棵树的影长为5.4米,请计算小明测量这棵树的高. 5.4ACA’C’ (2)同时小王在测另一棵树时,发现树影的一部分在地面上,而另一部分在墙上,他测得地面上的影长为2.7米,留在墙上部分的影长为1.2米.请计算小王测量的这棵树的高.2.7m1.2mBACD (2)同时小王在测另一棵树时,发现树影的一部分在地面上,而另一部分在墙上,他测得地面上的影长为2.7米,留在墙上部分的影长为1.2米.请计算小王测量的这棵树的高.
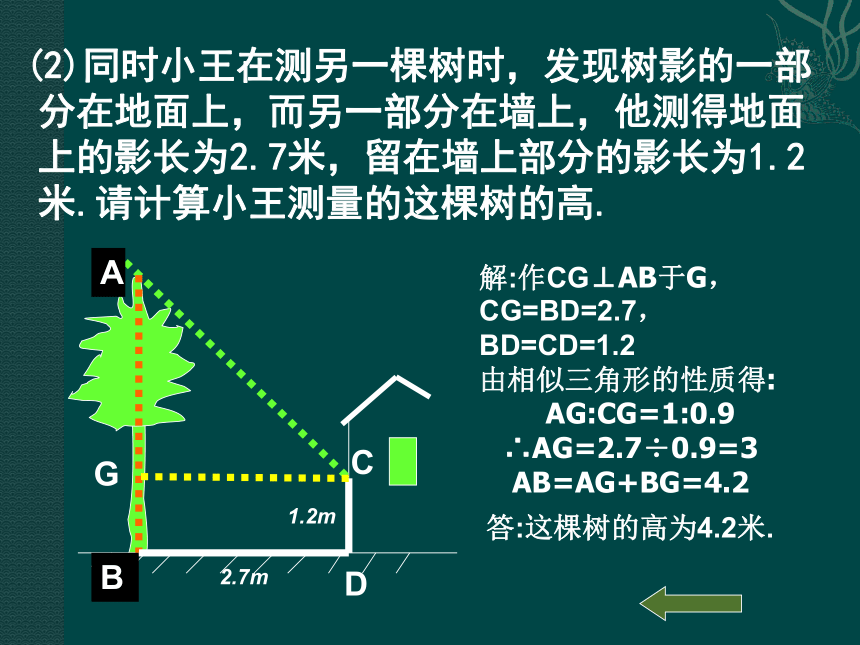
2.7m1.2mBAC解:作CG⊥AB于G, CG=BD=2.7,BD=CD=1.2 答:这棵树的高为4.2米.
DG由相似三角形的性质得: AG:CG=1:0.9 ∴AG=2.7÷0.9=3 AB=AG+BG=4.2 由相似三角形的性质得: BE 1
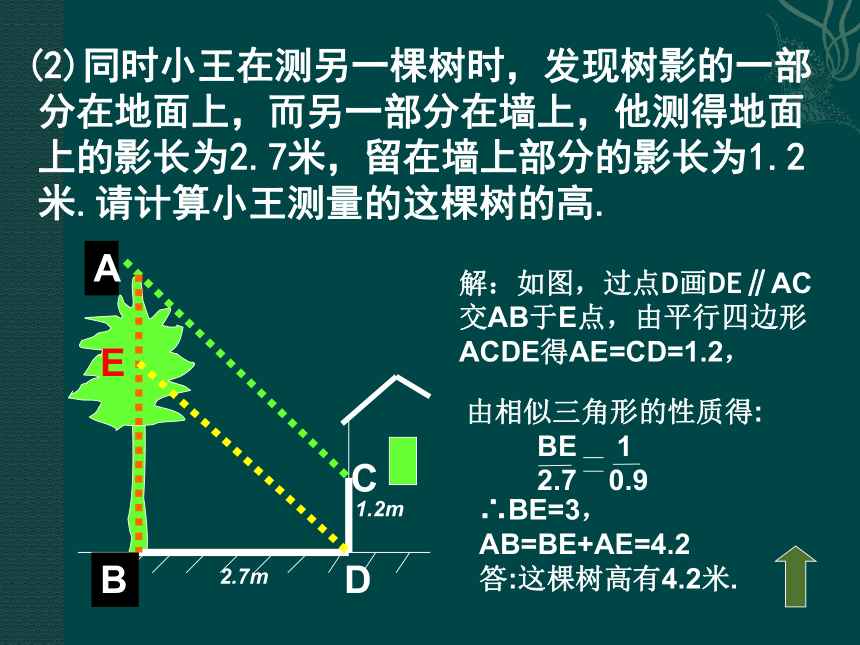
2.7 0.9 (2)同时小王在测另一棵树时,发现树影的一部分在地面上,而另一部分在墙上,他测得地面上的影长为2.7米,留在墙上部分的影长为1.2米.请计算小王测量的这棵树的高.2.7m1.2m解:如图,过点D画DE∥AC交AB于E点,由平行四边形ACDE得AE=CD=1.2,BADCE∴BE=3,AB=BE+AE=4.2 答:这棵树高有4.2米. (2)同时小王在测另一棵树时,发现树影的一部分在地面上,而另一部分在墙上,他测得地面上的影长为2.7米,留在墙上部分的影长为1.2米.请计算小王测量的这棵树的高.
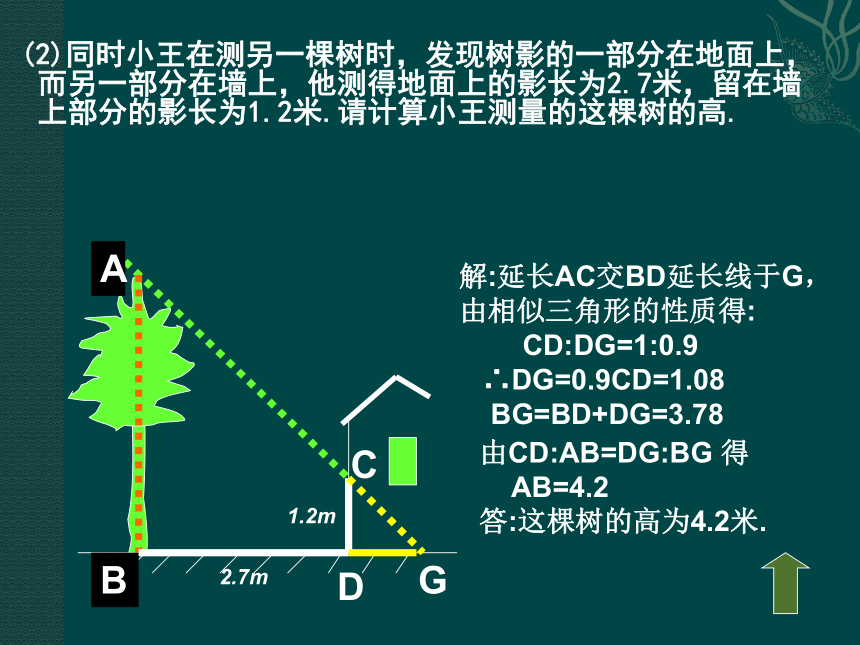
2.7m1.2mBAC解:延长AC交BD延长线于G, 由相似三角形的性质得: CD:DG=1:0.9 ∴DG=0.9CD=1.08 BG=BD+DG=3.78 由CD:AB=DG:BG 得 AB=4.2 答:这棵树的高为4.2米.
DG10mBACD4m30° (3)小明测得长为1米的竹竿影长为2米,同时,小李测量一棵树时发现树影的一部分在地面上,另一部分在斜坡的坡面上,测得在地面影长为10米,在斜坡上影长为4米,斜坡的倾斜角为30°,请计算这棵树的高. 10mBAC解:画CG⊥AB于G点,画CE ⊥BD于E,则
CE= CD=2, DE=2
∴BG=CE=2, BE=BD+DE=10+2 答:这棵树的高为(7+ )米.DG由相似三角形的性质得: AG:GC=1:2 ∴AG=5+ AB=BG+AG=7+4mE30° (3)小明测得长为1米的竹竿影长为2米,同时,小李测量一棵树时发现树影的一部分在地面上,另一部分在斜坡的坡面上,测得在地面影长为10米,在斜坡上影长为4米,斜坡的倾斜角为30°,请计算这棵树的高. (3)小明测得长为1米的竹竿影长为2米,同时,小李测量一棵树时发现树影的一部分在地面上,另一部分在斜坡的坡面上,测得在地面影长为10米,在斜坡上影长为4米,斜坡的倾斜角为30°,请计算这棵树的高. 10mBACDG4mE30° (3)小明测得长为1米的竹竿影长为2米,同时,小李测量一棵树时发现树影的一部分在地面上,另一部分在斜坡的坡面上,测得在地面影长为10米,在斜坡上影长为4米,斜坡的倾斜角为30°,请计算这棵树的高. 10mBACD4mEF30° (3)小明测得长为1米的竹竿影长为2米,同时,小李测量一棵树时发现树影的一部分在地面上,另一部分在斜坡的坡面上,测得在地面影长为10米,在斜坡上影长为4米,斜坡的倾斜角为30°,请计算这棵树的高. 10mBACDG4mEF30°胡夫金字塔是埃及现存规模最大的金字塔,被喻为“世界古代七大奇观之一”。塔的4个斜面正对东南西北四个方向,塔基呈正方形,每边长约230多米。据考证,为建成大金字塔,共动用了10万人花了20年时间.原高146.59米,但由于经过几千年的风吹雨打,顶端被风化吹蚀.所以高度有所降低 。 小小旅行家:走近金字塔小小考古家:古希腊数学家、天文学家泰勒斯游历古埃及时,只利用一根木棍和一把尺子就测量并计算出了金字塔的高度,你明白泰勒斯测量金字塔高度的道理了吗?木杆皮尺 小 结实际问题数学问题数学问题的解检验1.2. 数学思想方法: 化归思想3.通过构造三角形,利用相似三角形的
性质是求线段长度的常用方法.
4.相似三角形的应用主要有如下两个方面
(1)测高(不能直接使用皮尺或刻度尺量的)
(2)测距(不能直接测量的两点间的距离)测高的方法
测量不能到达顶部的物体的高度,通常用“在
同一时刻物高与影长的比例”的原理解决. 测距的方法
测量不能到达两点间的距离,常构造相似三角
形求解.
2.7m1.2mBAC解:作CG⊥AB于G, CG=BD=2.7,BD=CD=1.2 答:这棵树的高为4.2米.
DG由相似三角形的性质得: AG:CG=1:0.9 ∴AG=2.7÷0.9=3 AB=AG+BG=4.2 由相似三角形的性质得: BE 1
2.7 0.9 (2)同时小王在测另一棵树时,发现树影的一部分在地面上,而另一部分在墙上,他测得地面上的影长为2.7米,留在墙上部分的影长为1.2米.请计算小王测量的这棵树的高.2.7m1.2m解:如图,过点D画DE∥AC交AB于E点,由平行四边形ACDE得AE=CD=1.2,BADCE∴BE=3,AB=BE+AE=4.2 答:这棵树高有4.2米. (2)同时小王在测另一棵树时,发现树影的一部分在地面上,而另一部分在墙上,他测得地面上的影长为2.7米,留在墙上部分的影长为1.2米.请计算小王测量的这棵树的高.
2.7m1.2mBAC解:延长AC交BD延长线于G, 由相似三角形的性质得: CD:DG=1:0.9 ∴DG=0.9CD=1.08 BG=BD+DG=3.78 由CD:AB=DG:BG 得 AB=4.2 答:这棵树的高为4.2米.
DG10mBACD4m30° (3)小明测得长为1米的竹竿影长为2米,同时,小李测量一棵树时发现树影的一部分在地面上,另一部分在斜坡的坡面上,测得在地面影长为10米,在斜坡上影长为4米,斜坡的倾斜角为30°,请计算这棵树的高. 10mBAC解:画CG⊥AB于G点,画CE ⊥BD于E,则
CE= CD=2, DE=2
∴BG=CE=2, BE=BD+DE=10+2 答:这棵树的高为(7+ )米.DG由相似三角形的性质得: AG:GC=1:2 ∴AG=5+ AB=BG+AG=7+4mE30° (3)小明测得长为1米的竹竿影长为2米,同时,小李测量一棵树时发现树影的一部分在地面上,另一部分在斜坡的坡面上,测得在地面影长为10米,在斜坡上影长为4米,斜坡的倾斜角为30°,请计算这棵树的高. (3)小明测得长为1米的竹竿影长为2米,同时,小李测量一棵树时发现树影的一部分在地面上,另一部分在斜坡的坡面上,测得在地面影长为10米,在斜坡上影长为4米,斜坡的倾斜角为30°,请计算这棵树的高. 10mBACDG4mE30° (3)小明测得长为1米的竹竿影长为2米,同时,小李测量一棵树时发现树影的一部分在地面上,另一部分在斜坡的坡面上,测得在地面影长为10米,在斜坡上影长为4米,斜坡的倾斜角为30°,请计算这棵树的高. 10mBACD4mEF30° (3)小明测得长为1米的竹竿影长为2米,同时,小李测量一棵树时发现树影的一部分在地面上,另一部分在斜坡的坡面上,测得在地面影长为10米,在斜坡上影长为4米,斜坡的倾斜角为30°,请计算这棵树的高. 10mBACDG4mEF30°胡夫金字塔是埃及现存规模最大的金字塔,被喻为“世界古代七大奇观之一”。塔的4个斜面正对东南西北四个方向,塔基呈正方形,每边长约230多米。据考证,为建成大金字塔,共动用了10万人花了20年时间.原高146.59米,但由于经过几千年的风吹雨打,顶端被风化吹蚀.所以高度有所降低 。 小小旅行家:走近金字塔小小考古家:古希腊数学家、天文学家泰勒斯游历古埃及时,只利用一根木棍和一把尺子就测量并计算出了金字塔的高度,你明白泰勒斯测量金字塔高度的道理了吗?木杆皮尺 小 结实际问题数学问题数学问题的解检验1.2. 数学思想方法: 化归思想3.通过构造三角形,利用相似三角形的
性质是求线段长度的常用方法.
4.相似三角形的应用主要有如下两个方面
(1)测高(不能直接使用皮尺或刻度尺量的)
(2)测距(不能直接测量的两点间的距离)测高的方法
测量不能到达顶部的物体的高度,通常用“在
同一时刻物高与影长的比例”的原理解决. 测距的方法
测量不能到达两点间的距离,常构造相似三角
形求解.
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
