4.1圆的对称性(第3课时)圆心角,弧,弦,弦心距之间的关系
文档属性
| 名称 | 4.1圆的对称性(第3课时)圆心角,弧,弦,弦心距之间的关系 |

|
|
| 格式 | rar | ||
| 文件大小 | 469.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-11-14 00:00:00 | ||
图片预览



文档简介
课件15张PPT。 2. 圆的对称性(3)
圆心角,弧,弦,弦心距之间的关系九年级数学(上)第四章: 对圆的进一步认识学习目标了解圆的中心对称的性质。
探索并证明圆心角与其所对弧的关系定理,并能运用它们解决有关的实际问题。圆的对称性及特性圆是轴对称图形,圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.驶向胜利的彼岸圆也是中心对称图形,它的对称中心就是圆心.用旋转的方法可以得到:一个圆绕着它的圆心旋转任意一个角度,都能与原来的图形重合.这是圆特有的一个性质:圆的旋转不变性圆心角圆心角 顶点在圆心的角(如∠AOB).
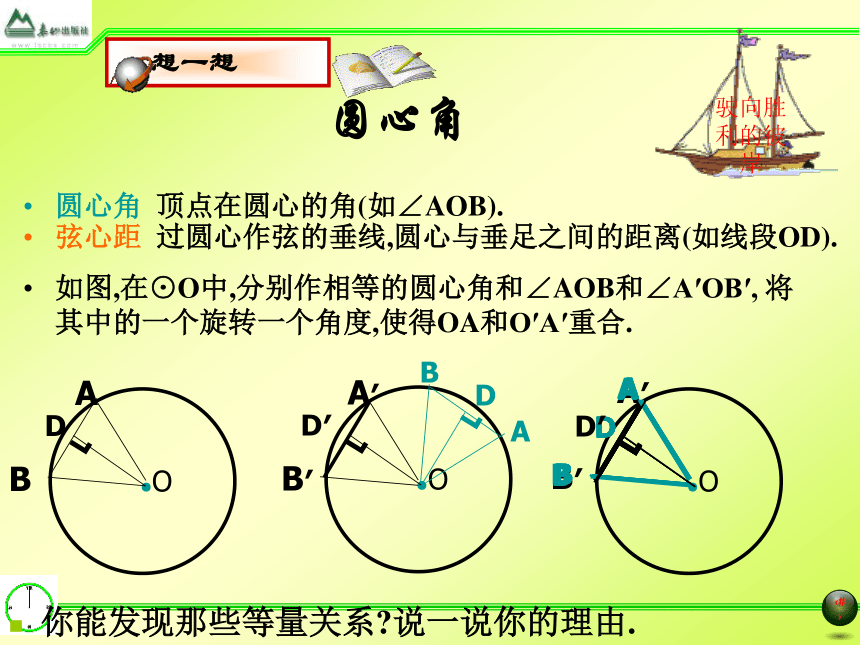
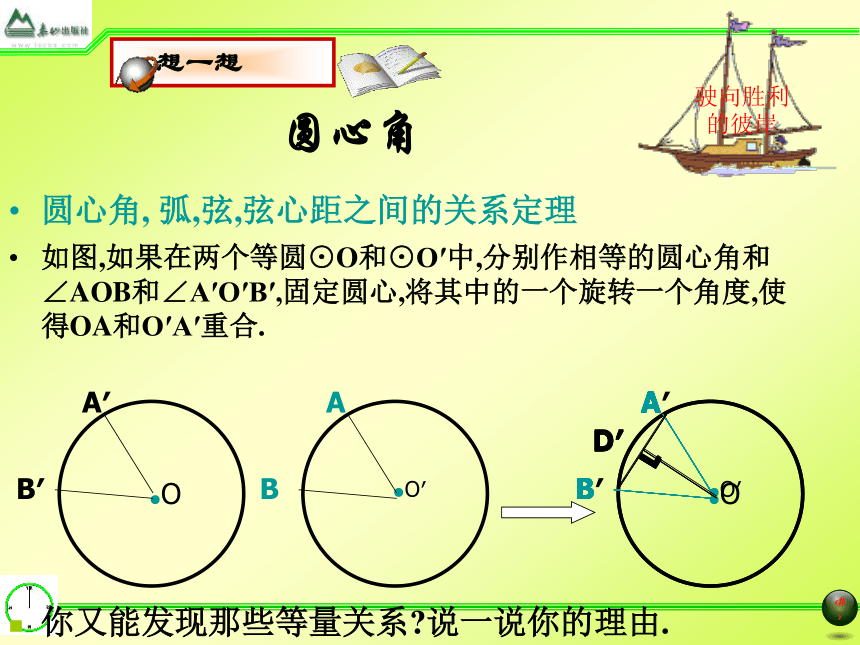
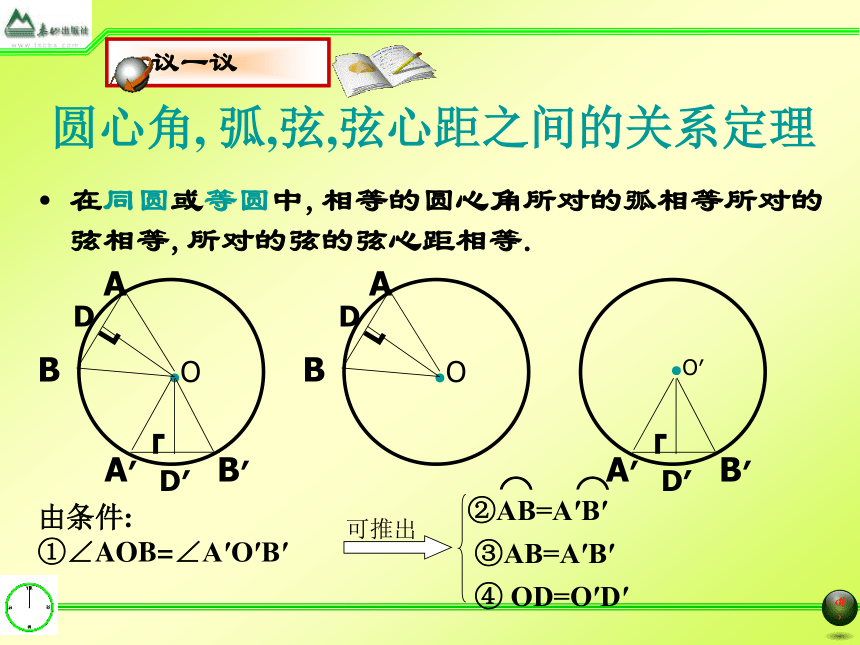
弦心距 过圆心作弦的垂线,圆心与垂足之间的距离(如线段OD).如图,在⊙O中,分别作相等的圆心角和∠AOB和∠A′OB′, 将其中的一个旋转一个角度,使得OA和O′A′重合.驶向胜利的彼岸 你能发现那些等量关系?说一说你的理由.圆心角圆心角, 弧,弦,弦心距之间的关系定理如图,如果在两个等圆⊙O和⊙O′中,分别作相等的圆心角和∠AOB和∠A′O′B′,固定圆心,将其中的一个旋转一个角度,使得OA和O′A′重合.驶向胜利的彼岸 你又能发现那些等量关系?说一说你的理由.圆心角, 弧,弦,弦心距之间的关系定理在同圆或等圆中,相等的圆心角所对的弧相等所对的弦相等,所对的弦的弦心距相等.由条件:
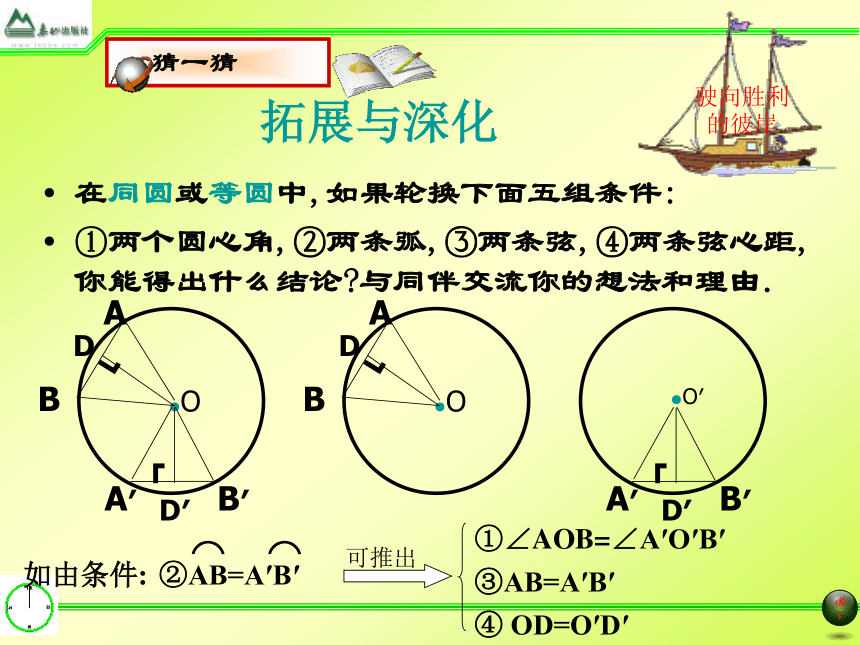
①∠AOB=∠A′O′B′③AB=A′B′④ OD=O′D′驶向胜利的彼岸拓展与深化在同圆或等圆中,如果轮换下面五组条件:
①两个圆心角,②两条弧,③两条弦,④两条弦心距,你能得出什么结论?与同伴交流你的想法和理由.如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′推论在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′推论如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′注意:在同圆或等圆中相等的弦所对的两条劣弧(优弧)相等,相等的劣弧(优弧)所对的圆心角相等。化心动为行动1.已知A,B是⊙O上的两点,∠AOB=1200,C是 的中点,试确定四边形OACB的形状,并说明理由.驶向胜利的彼岸2.利用一个圆及若干条弦分别设计出符合下列条件的图案:
(1)是轴对称图形但不是中心对称图形;
(2)即是轴对称图形又是中心对称图形.
3.日常生活中的许多图案或现象都与圆的对称性有关,试举几例.化心动为行动 课本第112页 练习
第1、2题驶向胜利的彼岸总 结: 亲爱的同学们,学习了这节课,你有何收获?你能用精炼的语言表达出来吗?总结一下?挑战自我习题4.1 5-7题祝你成功!驶向胜利的彼岸结束寄语你做成功一件事,千万不要等待着享受荣誉,应该再做那些需要做的事.再见
圆心角,弧,弦,弦心距之间的关系九年级数学(上)第四章: 对圆的进一步认识学习目标了解圆的中心对称的性质。
探索并证明圆心角与其所对弧的关系定理,并能运用它们解决有关的实际问题。圆的对称性及特性圆是轴对称图形,圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.驶向胜利的彼岸圆也是中心对称图形,它的对称中心就是圆心.用旋转的方法可以得到:一个圆绕着它的圆心旋转任意一个角度,都能与原来的图形重合.这是圆特有的一个性质:圆的旋转不变性圆心角圆心角 顶点在圆心的角(如∠AOB).
弦心距 过圆心作弦的垂线,圆心与垂足之间的距离(如线段OD).如图,在⊙O中,分别作相等的圆心角和∠AOB和∠A′OB′, 将其中的一个旋转一个角度,使得OA和O′A′重合.驶向胜利的彼岸 你能发现那些等量关系?说一说你的理由.圆心角圆心角, 弧,弦,弦心距之间的关系定理如图,如果在两个等圆⊙O和⊙O′中,分别作相等的圆心角和∠AOB和∠A′O′B′,固定圆心,将其中的一个旋转一个角度,使得OA和O′A′重合.驶向胜利的彼岸 你又能发现那些等量关系?说一说你的理由.圆心角, 弧,弦,弦心距之间的关系定理在同圆或等圆中,相等的圆心角所对的弧相等所对的弦相等,所对的弦的弦心距相等.由条件:
①∠AOB=∠A′O′B′③AB=A′B′④ OD=O′D′驶向胜利的彼岸拓展与深化在同圆或等圆中,如果轮换下面五组条件:
①两个圆心角,②两条弧,③两条弦,④两条弦心距,你能得出什么结论?与同伴交流你的想法和理由.如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′推论在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′推论如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′注意:在同圆或等圆中相等的弦所对的两条劣弧(优弧)相等,相等的劣弧(优弧)所对的圆心角相等。化心动为行动1.已知A,B是⊙O上的两点,∠AOB=1200,C是 的中点,试确定四边形OACB的形状,并说明理由.驶向胜利的彼岸2.利用一个圆及若干条弦分别设计出符合下列条件的图案:
(1)是轴对称图形但不是中心对称图形;
(2)即是轴对称图形又是中心对称图形.
3.日常生活中的许多图案或现象都与圆的对称性有关,试举几例.化心动为行动 课本第112页 练习
第1、2题驶向胜利的彼岸总 结: 亲爱的同学们,学习了这节课,你有何收获?你能用精炼的语言表达出来吗?总结一下?挑战自我习题4.1 5-7题祝你成功!驶向胜利的彼岸结束寄语你做成功一件事,千万不要等待着享受荣誉,应该再做那些需要做的事.再见
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
