新课标A版必修4.1.3 诱导公式
文档属性
| 名称 | 新课标A版必修4.1.3 诱导公式 |  | |
| 格式 | rar | ||
| 文件大小 | 65.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-11-12 18:42:00 | ||
图片预览

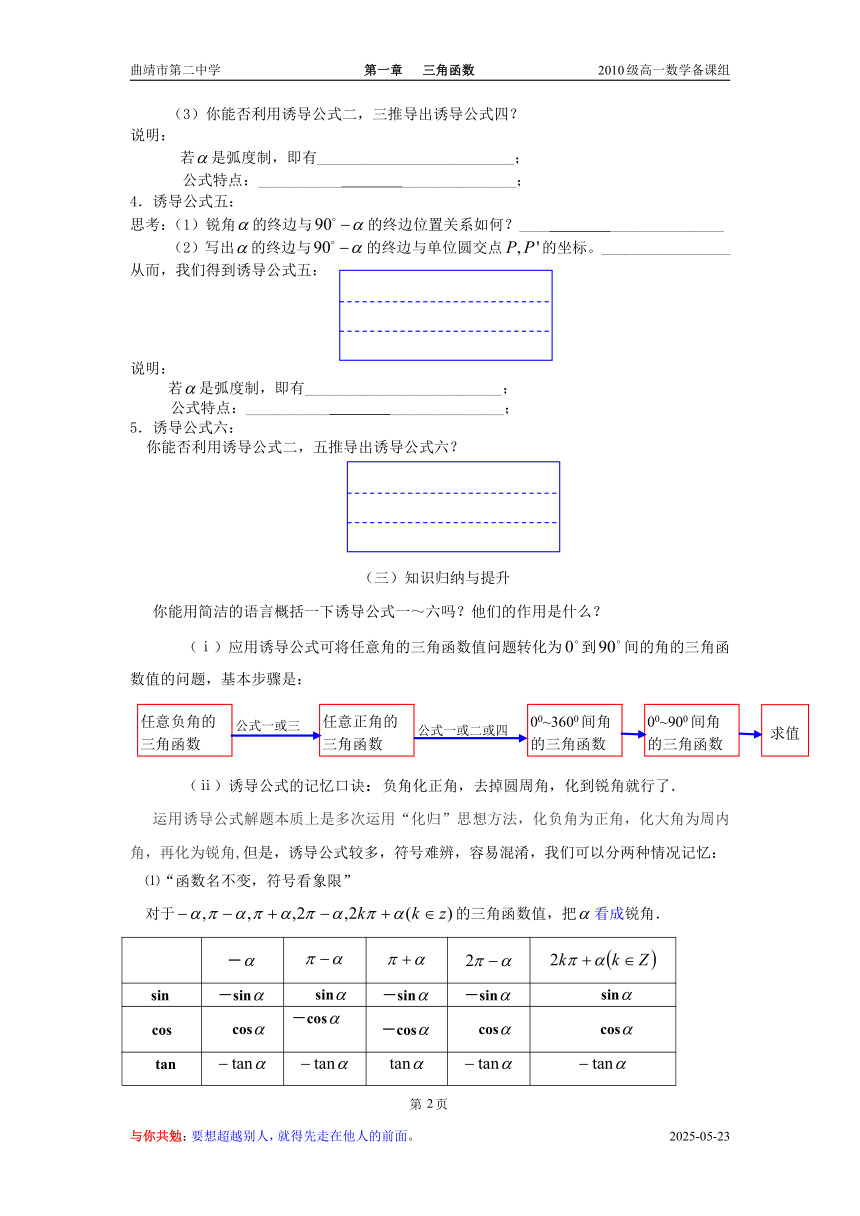
文档简介
曲靖市第二中学 第一章 三角函数 2010级高一数学备课组
1.3 诱导公式
一、导学目标
(1)能推导诱导公式一、二、三、四、五、六.
(2)掌握诱导公式并运用之进行三角函数式的求值、化简以及简单三角恒等式的证明.
二、尝试练习
(一)知识回顾
1.,,是如何定义的?
2.三角函数在各个象限的取值符号如何?___________ ______________ _
___________ ______________ _________ ______________ 3.诱导公式(一) 终边相同的角的同一三角函数的值相等,即
(二)新课导学
1.诱导公式二:
思考:(1)锐角的终边与的终边位置关系如何?____ _______________
(2) 写出的终边与的终边与单位圆交点的坐标。________________
从而,我们得到诱导公式二:
说明:
若是弧度制,即有__________________________;
公式特点:___________ _______________;
2.诱导公式三:
思考: (1)的终边与的终边位置关系如何?____________ _____
(2) 角与的终边位置关系如何?_____________ _______
从而,我们得到诱导公式三:
3.诱导公式四:
思考:(1)锐角的终边与的终边位置关系如何?____ _______________
(2)写出的终边与的终边与单位圆交点的坐标。_________________从而,我们得到诱导公式四:
(3)你能否利用诱导公式二,三推导出诱导公式四?
说明:
若是弧度制,即有__________________________;
公式特点:___________ _______________;
4.诱导公式五:
思考:(1)锐角的终边与的终边位置关系如何?____ _______________
(2)写出的终边与的终边与单位圆交点的坐标。_________________从而,我们得到诱导公式五:
说明:
若是弧度制,即有__________________________;
公式特点:___________ _______________;
5.诱导公式六:
你能否利用诱导公式二,五推导出诱导公式六?
(三)知识归纳与提升
你能用简洁的语言概括一下诱导公式一~六吗?他们的作用是什么?
(ⅰ)应用诱导公式可将任意角的三角函数值问题转化为到间的角的三角函数值的问题,基本步骤是:
(ⅱ)诱导公式的记忆口诀:负角化正角,去掉圆周角,化到锐角就行了.
运用诱导公式解题本质上是多次运用“化归”思想方法,化负角为正角,化大角为周内角,再化为锐角,但是,诱导公式较多,符号难辨,容易混淆,我们可以分两种情况记忆:[来
⑴“函数名不变,符号看象限”
对于的三角函数值,把看成锐角.
-
sin21 -sin sin -sin -sin sin
cos cos -cos21世纪教育网 -cos cos cos
tan
⑵“函数名改变,符号看象限”
对于的三角函数值,把看成锐角.
sin
cos
⑶ 以上两种情况可归结为“”的三角函数值,口诀为
(四)我也能行
1.(1998全国—理1) sin600 的值是 ( )
A. B.- C. D.-
2.(07全国2 —理1)sin2100 = ( )
A. B.- C. D .-
3.(07湖北—文1)tan690°的值为 ( )
A.- B. C. D.
4.已知,那么的值为 ( )
A ( http: / / wxc. ) B ( http: / / wxc. ) C ( http: / / wxc. ) D ( http: / / wxc. )
三、精点精评
例1.求下列三角函数值:(1); (2).
例2.(1)已知,且是第四象限角,求的值.
(2)已知:,求的值.
例3. 求证.
四、直击高考
1. (2010全国Ⅰ—文1)
A. B.- C. D.
2. (2010全国Ⅰ—理2)记,那么
A. B.- C. D.-
3. (2005湖南)tan600°的值是 ( )
A. B. C. D.
4. 已知,且是第四象限角,那么的值是 ( )
A ( http: / / wxc. ) B ( http: / / wxc. ) C ( http: / / wxc. ) D ( http: / / wxc. )
5. (2010全国Ⅱ—文13)已知是第二象限的角,,则=___________.
6. 已知,求的值.
我的留言
公式一或二或四
任意负角的
三角函数
任意正角的
三角函数
00~3600间角
的三角函数
00~900间角
的三角函数
求值
公式一或三
PAGE
4
第 页
与你共勉:要想超越别人,就得先走在他人的前面。 2010-11-12
1.3 诱导公式
一、导学目标
(1)能推导诱导公式一、二、三、四、五、六.
(2)掌握诱导公式并运用之进行三角函数式的求值、化简以及简单三角恒等式的证明.
二、尝试练习
(一)知识回顾
1.,,是如何定义的?
2.三角函数在各个象限的取值符号如何?___________ ______________ _
___________ ______________ _________ ______________ 3.诱导公式(一) 终边相同的角的同一三角函数的值相等,即
(二)新课导学
1.诱导公式二:
思考:(1)锐角的终边与的终边位置关系如何?____ _______________
(2) 写出的终边与的终边与单位圆交点的坐标。________________
从而,我们得到诱导公式二:
说明:
若是弧度制,即有__________________________;
公式特点:___________ _______________;
2.诱导公式三:
思考: (1)的终边与的终边位置关系如何?____________ _____
(2) 角与的终边位置关系如何?_____________ _______
从而,我们得到诱导公式三:
3.诱导公式四:
思考:(1)锐角的终边与的终边位置关系如何?____ _______________
(2)写出的终边与的终边与单位圆交点的坐标。_________________从而,我们得到诱导公式四:
(3)你能否利用诱导公式二,三推导出诱导公式四?
说明:
若是弧度制,即有__________________________;
公式特点:___________ _______________;
4.诱导公式五:
思考:(1)锐角的终边与的终边位置关系如何?____ _______________
(2)写出的终边与的终边与单位圆交点的坐标。_________________从而,我们得到诱导公式五:
说明:
若是弧度制,即有__________________________;
公式特点:___________ _______________;
5.诱导公式六:
你能否利用诱导公式二,五推导出诱导公式六?
(三)知识归纳与提升
你能用简洁的语言概括一下诱导公式一~六吗?他们的作用是什么?
(ⅰ)应用诱导公式可将任意角的三角函数值问题转化为到间的角的三角函数值的问题,基本步骤是:
(ⅱ)诱导公式的记忆口诀:负角化正角,去掉圆周角,化到锐角就行了.
运用诱导公式解题本质上是多次运用“化归”思想方法,化负角为正角,化大角为周内角,再化为锐角,但是,诱导公式较多,符号难辨,容易混淆,我们可以分两种情况记忆:[来
⑴“函数名不变,符号看象限”
对于的三角函数值,把看成锐角.
-
sin21 -sin sin -sin -sin sin
cos cos -cos21世纪教育网 -cos cos cos
tan
⑵“函数名改变,符号看象限”
对于的三角函数值,把看成锐角.
sin
cos
⑶ 以上两种情况可归结为“”的三角函数值,口诀为
(四)我也能行
1.(1998全国—理1) sin600 的值是 ( )
A. B.- C. D.-
2.(07全国2 —理1)sin2100 = ( )
A. B.- C. D .-
3.(07湖北—文1)tan690°的值为 ( )
A.- B. C. D.
4.已知,那么的值为 ( )
A ( http: / / wxc. ) B ( http: / / wxc. ) C ( http: / / wxc. ) D ( http: / / wxc. )
三、精点精评
例1.求下列三角函数值:(1); (2).
例2.(1)已知,且是第四象限角,求的值.
(2)已知:,求的值.
例3. 求证.
四、直击高考
1. (2010全国Ⅰ—文1)
A. B.- C. D.
2. (2010全国Ⅰ—理2)记,那么
A. B.- C. D.-
3. (2005湖南)tan600°的值是 ( )
A. B. C. D.
4. 已知,且是第四象限角,那么的值是 ( )
A ( http: / / wxc. ) B ( http: / / wxc. ) C ( http: / / wxc. ) D ( http: / / wxc. )
5. (2010全国Ⅱ—文13)已知是第二象限的角,,则=___________.
6. 已知,求的值.
我的留言
公式一或二或四
任意负角的
三角函数
任意正角的
三角函数
00~3600间角
的三角函数
00~900间角
的三角函数
求值
公式一或三
PAGE
4
第 页
与你共勉:要想超越别人,就得先走在他人的前面。 2010-11-12
