直角三角形全等的判定

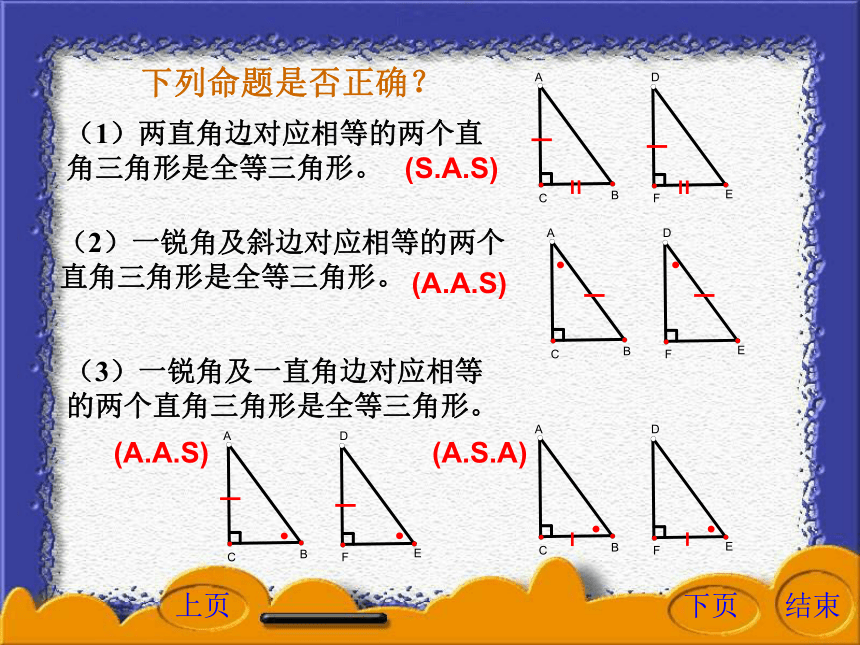
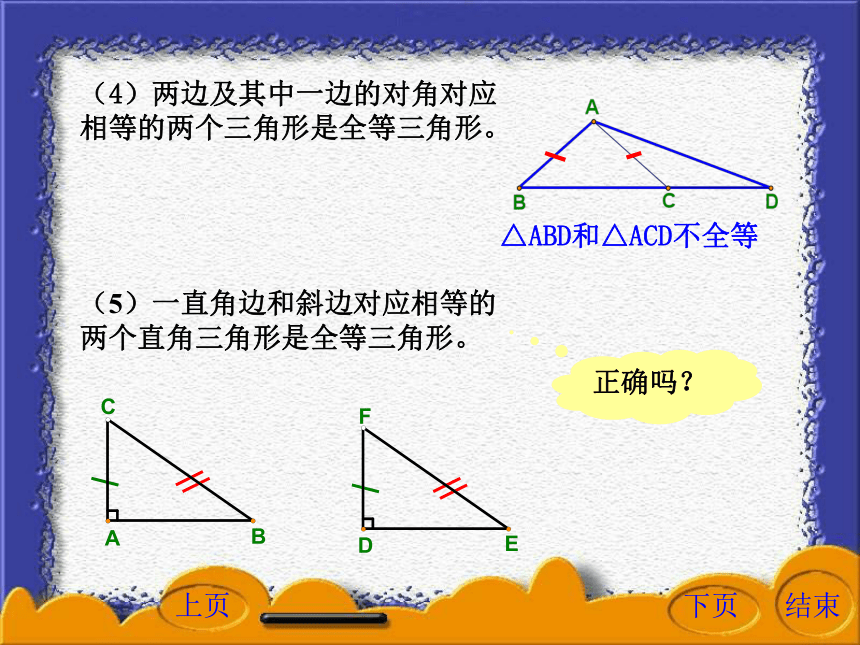
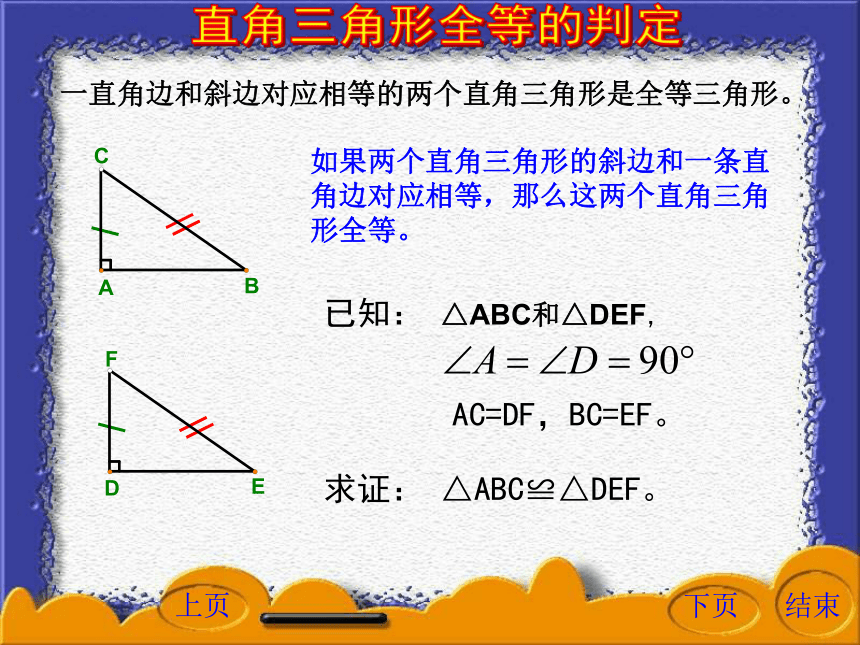
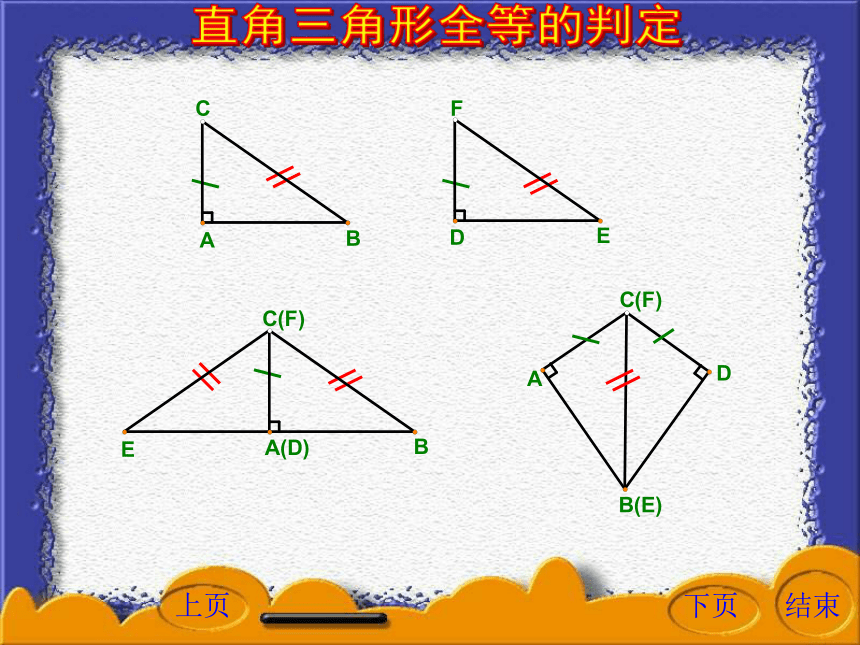
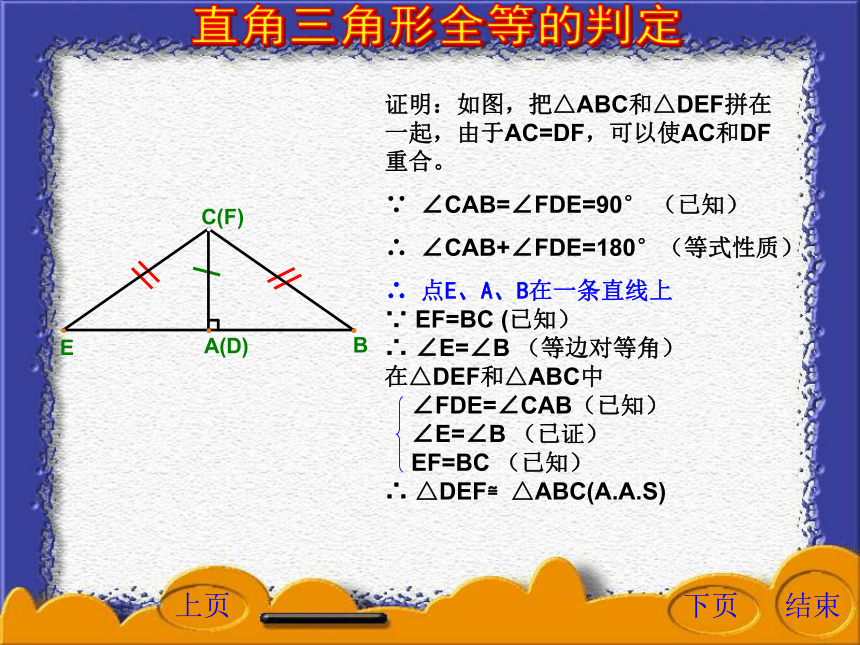
课件16张PPT。下列命题是否正确？（2）一锐角及斜边对应相等的两个直角三角形是全等三角形。（1）两直角边对应相等的两个直角三角形是全等三角形。（3）一锐角及一直角边对应相等的两个直角三角形是全等三角形。(S.A.S)(A.S.A)(A.A.S)(A.A.S)（5）一直角边和斜边对应相等的两个直角三角形是全等三角形。正确吗？（4）两边及其中一边的对角对应相等的两个三角形是全等三角形。△ABD和△ACD不全等直角三角形全等的判定一直角边和斜边对应相等的两个直角三角形是全等三角形。已知： △ABC和△DEF,求证： △ABC≌△DEF。AC=DF，BC=EF。如果两个直角三角形的斜边和一条直角边对应相等，那么这两个直角三角形全等。直角三角形全等的判定直角三角形全等的判定证明：如图，把△ABC和△DEF拼在一起，由于AC=DF，可以使AC和DF重合。
∵ ∠CAB=∠FDE=90° （已知）
∴ ∠CAB+∠FDE=180°（等式性质）
∴ 点E、A、B在一条直线上
∵ EF=BC (已知）
∴ ∠E=∠B （等边对等角）
在△DEF和△ABC中
∠FDE=∠CAB（已知）
∠E=∠B （已证）
EF=BC （已知）
∴ △DEF≌△ABC(A.A.S)
直角三角形全等的判定证明：如图，把△ABC和△DEF拼在一起，由于BC=EF，可以使BC和EF重合。连接AD.
∵ AC=DF (已知）
∴ ∠1=∠2 （等边对等角）
∵ ∠CAB=∠FDE=90° （已知）
∴ ∠CAB －∠1 =∠FDE －∠２（等式性质）
即 ∠3 = ∠4
∴ AB=DE (等角对等边）
在△ABC和△DEF中
AC=DF （已知）
∠CAB=∠FDE （已知）
AB=DE （已证）
∴ △ABC≌△DEF(S.A.S)1234直角三角形全等的判定直角三角形全等的判定定理：如果两个直角三角形的斜边和一条直角边对应相等，那么这两个直角三角形全等。简记为 H.L在Rt△ABC与Rt△DEF中，AC=DF( )
BC=EF( )∴ Rt△ABC≌Rt△DEF(H.L) 直角三角形全等的判定例题 如图，已知：∠C=∠D=90°，BC=BD。
求证：△ABC≌△ABD在Rt△ABC与Rt△ABD中，BC=BD( 已知 )
AB=AB( 公共边 )∴ Rt△ABC≌Rt△ABD(H.L) 证明：∵ ∠C=∠D=90° （已知）
∴ △ABC和△ABD都是直角三角形直角三角形全等的判定直角三角形全等的判定定理： 如果两个直角三角形的斜边和一条直角边对应相等，那么这两个直角三角形全等。简记为H.L。练习： 如图，已知：∠C=∠D=90°，要得到△ABC≌△BAD，需添加一个条件。请写出添加的条件，并说明两个三角形全等的判定方法。添加____________，判定方法是_____。添加____________，判定方法是_____。添加____________，判定方法是_____。添加____________，判定方法是_____。BC=ADH.LH.LAC=BD∠CBA=∠DAB∠CAB=∠DBAA.A.SA.A.S直角三角形全等的判定直角三角形全等的判定定理： 如果两个直角三角形的斜边和一条直角边对应相等，那么这两个直角三角形全等。简记为H.L。(S.A.S)(A.S.A)(A.A.S)(H.L)直角三角形全等的判定例题： 已知：如图，△ABC中，DE⊥AB，DF⊥AC， ∠1=∠2，BD=CD。
求证：EB=FC12直角三角形全等的判定你能说出图中共有几对全等三角形吗？你能证明△ABC是等腰三角形吗？直角三角形全等的判定定理： 如果两个直角三角形的斜边和一条直角边对应相等，那么这两个直角三角形全等。简记为H.L。变式2 已知：如图，△ABC中，DE⊥AB，DF⊥AC， ∠1=∠2， EB=FC 。
求证： BD=CD12变式1 已知：如图，△ABC中，DE⊥AB，DF⊥AC， BD=CD ， EB=FC 。
求证： ∠1=∠212直角三角形全等的判定直角三角形全等的判定定理： 如果两个直角三角形的斜边和一条直角边对应相等，那么这两个直角三角形全等。简记为H.L。小结
学习了……
体会了……
直角三角形全等的判定作业：
必做题：课本第114页练习19.7/3
选做题：如何用一块三角板作出已知角的平分线？直角三角形全等的判定