相似三角形
图片预览




文档简介
课件15张PPT。三角形的中位线方城县博望 二初中 张冬教学目标知识与技能:理解三角形中位线定义与性质,会应用三角形中位线解决实际问题.
过程与方法:经历探究三角形中位线定义、性质的过程,感受三角形中位线定理的应用思想。
情感、态度与价值观:培养良好的探究意识和合作交流的习惯,体会数学推理的应用价值.
1.如图,A、B两点被池塘隔开,现在要测量出A、B两点间的距离 ,但又无法直接去测量,怎么办?这时,在A、B外选一点C,连结AC和BC,并分别找出AC和BC的中点D、E,如果能测量出DE的长度,也就能知道AB的距离了。这是什么道理呢?今天这堂课我们就要来探究其中的学问。 ABCDE
1、问题牵引:已知:如图,在 中,DE‖BC求证:
知识回顾点拔:应用相似三角形判定方法,解决问题。
引导学生完成。
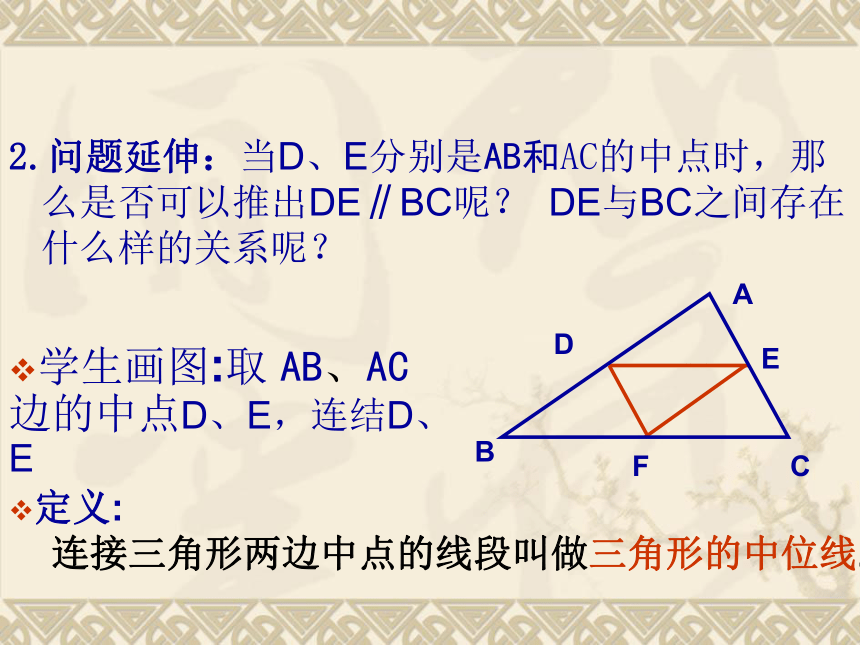
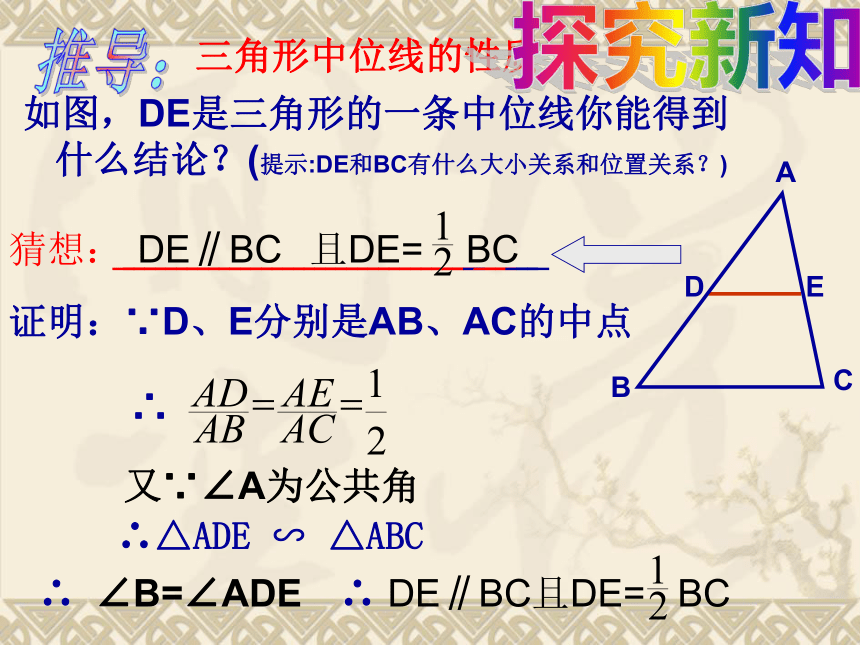
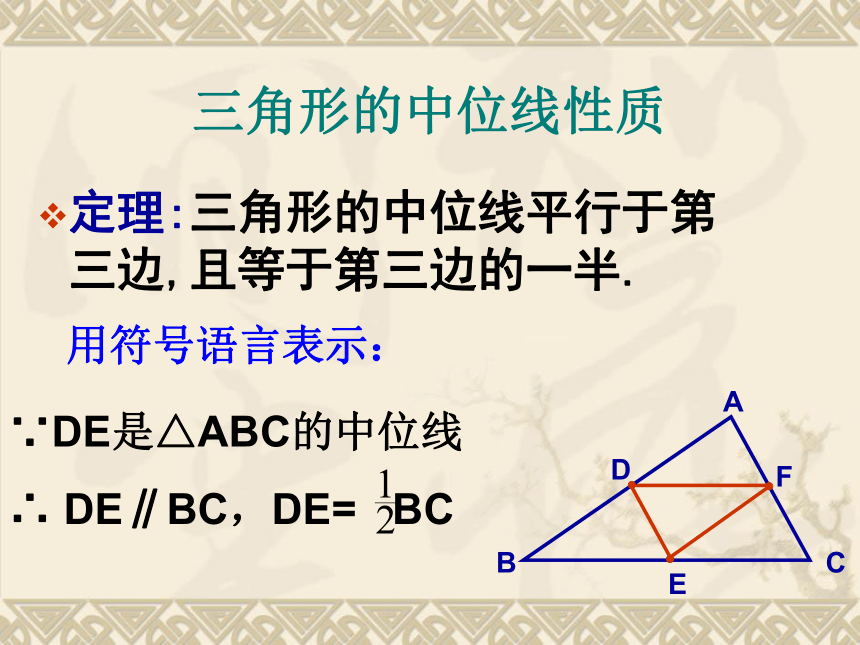
2.问题延伸:当D、E分别是AB和AC的中点时,那么是否可以推出DE∥BC呢? DE与BC之间存在什么样的关系呢?学生画图:取 AB、AC边的中点D、E,连结D、EABCDEF定义: 连接三角形两边中点的线段叫做三角形的中位线.三角形中位线的性质如图,DE是三角形的一条中位线你能得到什么结论?(提示:DE和BC有什么大小关系和位置关系?)猜想:? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?DE∥BC 且DE= BC推导:证明:∵D、E分别是AB、AC的中点∴又∵∠A为公共角∴△ADE ∽ △ABC ∴ ∠B=∠ADE∴ DE∥BC且DE= BC探究新知三角形的中位线性质定理:三角形的中位线平行于第三边,且等于第三边的一半.用符号语言表示:∵DE是△ABC的中位线
∴ DE∥BC,DE= BC例1、求证三角形的一条中位线与第三边的中线互相平分ABCDFE已知:如图所示,在△ABC中AD=DB,AF=FC,BE=EC 求证:AE、DF互相平分 证明:连结DE、EF∵ D、E、F分别为AB、BC、AC上中点∴DE、EF为△ABC的中位线DE ∥ AF、AD ∥EF四边形ADEF是平行四边形 ∴AE、DF互相平分范例学习,加强理解点拔:根据中线定义知道点E是BC的中点,因此连结DE、EF,再利用三角形的中位线得出四边形ADEF是平行四边形,从而得出结论。
如图所示, △ABC中,D、E分别是边BC、AB的中点,AD、CE相交于G,求证:BDGACE例2:点拔:点D、E分别是BC、AB的中点,应用中位线,
首先要构建中位线,这种辅助线就是自己引出,连结ED。学生自己完成推理过程。
∴
如图,任意作一个四边形,并将其四边的中点依次连接起来,得到一个新的四边形,这个新四边形的形状有什么特征?FG∥BD且FG= BD 四边形EFGH是平行四边形∴ EH∥FG且EH= FG∴四边形EHGF是平形四边形解:∵ EH∥BD且EH= BD
连结BD知识拓展⑴顺次连接任意四边形、平行四边形四边中点所得的四边形是平行四边形顺次连接平行四边形 、矩形的四边中点所得的四边形是什么形状?为什么? 如果将“矩形”改成“菱形”呢?正方形呢?⑵顺次连接矩形的四边中点所得的四边形是菱形⑶顺次连接菱形的四边中点所得的四边形是矩形结论: (4)顺次连接正方形形的四边中点所得的四边形是正方形。议一议1。如图(1)ΔABC中,
AB=6㎝, AC=8㎝,BC=10㎝,
D﹑E﹑F分别是ABACBC的中点
则ΔDEF的周长是____ ,
面积是____。 2.如图(2)ΔABC中,DE是
中位线,AF是中线,则DE与
AF的关系是____3.若顺次连接四边形四边中
点所得的四边形是菱形,则
原四边形( )
(A)一定是矩形 (B)一定是菱形
(C)对角线一定互相垂直 (D)对角线一定相等
FACBDEF(2)互相平分6cm212cmD课堂练习,加强运用小结三角形中位线定义:连接三角形两边中点的线段叫做三角形的中位线.
三角形中位线性质:三角形的中位线平行于第三边,且等于第三边的一半.能应用三角形中位线的性质解决有关计算或说理等问题。
作业 课 本 练习第1题、习题3、4题;
过程与方法:经历探究三角形中位线定义、性质的过程,感受三角形中位线定理的应用思想。
情感、态度与价值观:培养良好的探究意识和合作交流的习惯,体会数学推理的应用价值.
1.如图,A、B两点被池塘隔开,现在要测量出A、B两点间的距离 ,但又无法直接去测量,怎么办?这时,在A、B外选一点C,连结AC和BC,并分别找出AC和BC的中点D、E,如果能测量出DE的长度,也就能知道AB的距离了。这是什么道理呢?今天这堂课我们就要来探究其中的学问。 ABCDE
1、问题牵引:已知:如图,在 中,DE‖BC求证:
知识回顾点拔:应用相似三角形判定方法,解决问题。
引导学生完成。
2.问题延伸:当D、E分别是AB和AC的中点时,那么是否可以推出DE∥BC呢? DE与BC之间存在什么样的关系呢?学生画图:取 AB、AC边的中点D、E,连结D、EABCDEF定义: 连接三角形两边中点的线段叫做三角形的中位线.三角形中位线的性质如图,DE是三角形的一条中位线你能得到什么结论?(提示:DE和BC有什么大小关系和位置关系?)猜想:? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?DE∥BC 且DE= BC推导:证明:∵D、E分别是AB、AC的中点∴又∵∠A为公共角∴△ADE ∽ △ABC ∴ ∠B=∠ADE∴ DE∥BC且DE= BC探究新知三角形的中位线性质定理:三角形的中位线平行于第三边,且等于第三边的一半.用符号语言表示:∵DE是△ABC的中位线
∴ DE∥BC,DE= BC例1、求证三角形的一条中位线与第三边的中线互相平分ABCDFE已知:如图所示,在△ABC中AD=DB,AF=FC,BE=EC 求证:AE、DF互相平分 证明:连结DE、EF∵ D、E、F分别为AB、BC、AC上中点∴DE、EF为△ABC的中位线DE ∥ AF、AD ∥EF四边形ADEF是平行四边形 ∴AE、DF互相平分范例学习,加强理解点拔:根据中线定义知道点E是BC的中点,因此连结DE、EF,再利用三角形的中位线得出四边形ADEF是平行四边形,从而得出结论。
如图所示, △ABC中,D、E分别是边BC、AB的中点,AD、CE相交于G,求证:BDGACE例2:点拔:点D、E分别是BC、AB的中点,应用中位线,
首先要构建中位线,这种辅助线就是自己引出,连结ED。学生自己完成推理过程。
∴
如图,任意作一个四边形,并将其四边的中点依次连接起来,得到一个新的四边形,这个新四边形的形状有什么特征?FG∥BD且FG= BD 四边形EFGH是平行四边形∴ EH∥FG且EH= FG∴四边形EHGF是平形四边形解:∵ EH∥BD且EH= BD
连结BD知识拓展⑴顺次连接任意四边形、平行四边形四边中点所得的四边形是平行四边形顺次连接平行四边形 、矩形的四边中点所得的四边形是什么形状?为什么? 如果将“矩形”改成“菱形”呢?正方形呢?⑵顺次连接矩形的四边中点所得的四边形是菱形⑶顺次连接菱形的四边中点所得的四边形是矩形结论: (4)顺次连接正方形形的四边中点所得的四边形是正方形。议一议1。如图(1)ΔABC中,
AB=6㎝, AC=8㎝,BC=10㎝,
D﹑E﹑F分别是ABACBC的中点
则ΔDEF的周长是____ ,
面积是____。 2.如图(2)ΔABC中,DE是
中位线,AF是中线,则DE与
AF的关系是____3.若顺次连接四边形四边中
点所得的四边形是菱形,则
原四边形( )
(A)一定是矩形 (B)一定是菱形
(C)对角线一定互相垂直 (D)对角线一定相等
FACBDEF(2)互相平分6cm212cmD课堂练习,加强运用小结三角形中位线定义:连接三角形两边中点的线段叫做三角形的中位线.
三角形中位线性质:三角形的中位线平行于第三边,且等于第三边的一半.能应用三角形中位线的性质解决有关计算或说理等问题。
作业 课 本 练习第1题、习题3、4题;
