初中数学 华师大版 八年级上册 勾股定理
文档属性
| 名称 | 初中数学 华师大版 八年级上册 勾股定理 |

|
|
| 格式 | rar | ||
| 文件大小 | 18.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-11-18 16:08:00 | ||
图片预览

文档简介
14.1勾股定理(1)
一、教学目的:
1、知识目标:
掌握勾股定理,了解利用拼图验证勾股定理的方法,会初步运用勾股定理进
行简单的计算和实际应用。
2、能力目标:
通过勾股定理的学习,使学生再次体会由特殊到一般,由具体到抽象的认识规律,培养学生推理、发现、分析动手及解决实际问题的能力。
3、情感目标:
通过勾股定理的教学,介绍我国古代人民在勾股定理研究方面的成就,激发学生的爱国热情。
二、教学重点
对勾股定理的理解和实际应用。
三、教学难点
在勾股定理的探索和验证过程中,进一步体会数形结合思想。
四、教具准备
多媒体课件
五、教学过程
导入新课
2002年在北京召开的国际数学大会上,到处可以看到这个简洁优美的图案(如图),这个远看像旋转的风车的图案是采用了1700多年前中国数学家赵爽用来证明勾股定理的弦图。
作为国际数学大会的会标,它为什么有如此大的魅力呢?它蕴含着怎样的奥妙呢?这节课就带领大家一起探索勾股定理。
推进新课
新知探求
1.观察归纳
(1)观察图1-1
正方形A中含有 个小方格,即A的面积是 个单位面积。
正方形B的面积是 个单位面积。
正方形C的面积是 个单位面积。
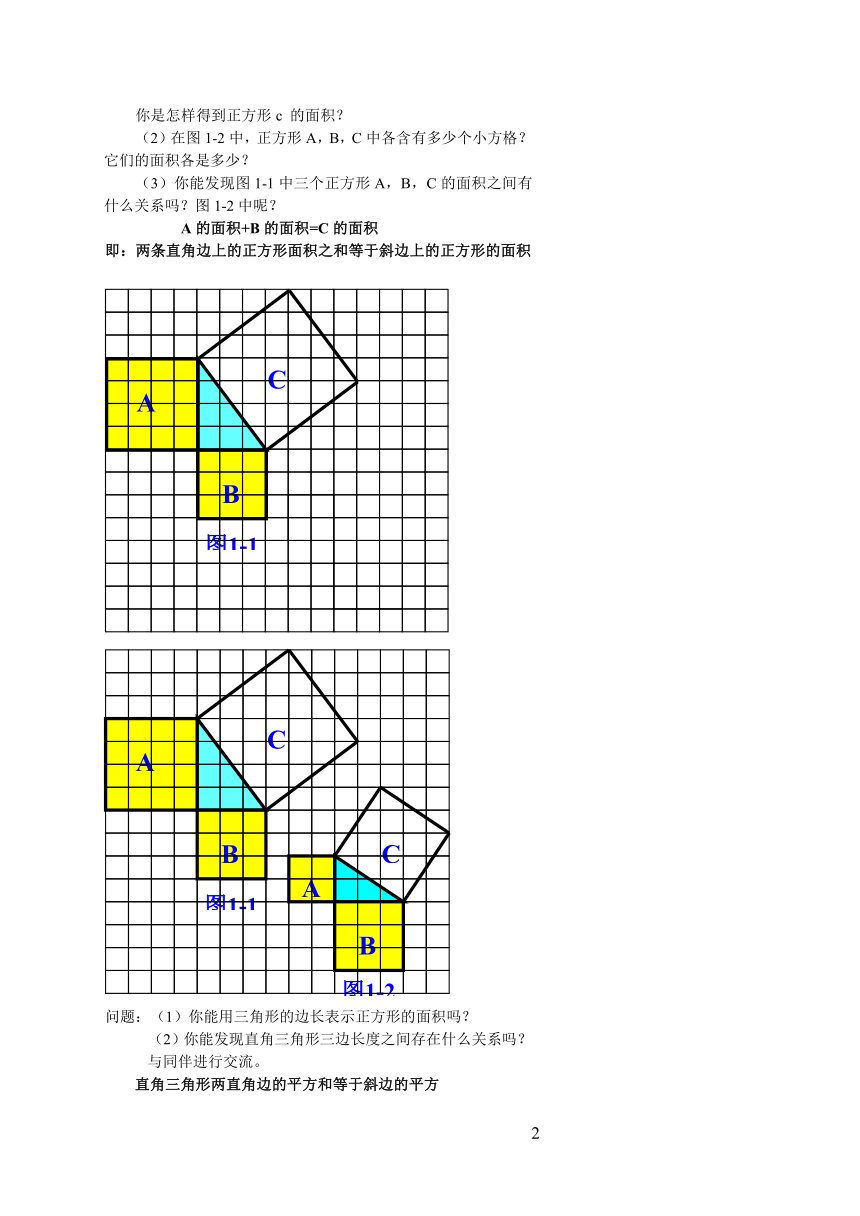
你是怎样得到正方形c 的面积?
(2)在图1-2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?
(3)你能发现图1-1中三个正方形A,B,C的面积之间有什么关系吗?图1-2中呢?
A的面积+B的面积=C的面积
即:两条直角边上的正方形面积之和等于斜边上的正方形的面积
问题:(1)你能用三角形的边长表示正方形的面积吗?
(2)你能发现直角三角形三边长度之间存在什么关系吗?与同伴进行交流。
直角三角形两直角边的平方和等于斜边的平方
2.实践验证
分别以5厘米、12厘米为直角边作出一个直角三角形,并测量斜边的长度。
(2)中的规律对这个三角形仍然成立吗?
3.总结
勾股定理(gou-gu theorem)
如果直角三角形两直角边分别为a、b,斜边为c,那么
a+b=c
即:直角三角形两直角边的平方和等于斜边的平方。
4.结论变形
直角三角形中,两直角边的平方和等于斜边的平方;
那么a+b=c 也就有:
应用示例
例1:如图:将长为5.41米的梯子AC斜靠在墙上,BC长为2.16米,求梯子上端A到墙的底边的垂直距离AB.(精确到0.01米)
图14.1.4
解 如图14.1.4,在Rt△ABC中,
BC=2.16米, AC=5.41米,
根据勾股定理可得
AB==≈4.96(米).
答: 梯子上端A到墙的底边的垂直距离 AB 约为4.96米.
例2:小明妈妈买了一部29英寸(74厘米)的电视机,小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗?
随堂练习
求出下列直角三角形中未知边的长度
小结
1、利用数格子的方法,探索了以直角三角形三边为边长的正方形面积的关系(即两个小正方形的面积之和等于大正方形的面积)
2、探索了直角三角形的三边关系,得到勾股定理:
即直角三角形两直角边的平方和等于斜边的平方
注意:应用勾股定理时应特别注意哪个角是直角。
作业
1. P55 第 2题
2.在直角三角形ABC中, ∠C=90°,
(1)已知: a=5, b=12, 求c;
(2)已知: b=6,c=10 , 求a;
3.准备四张形状相同大小一样的直角三角形硬纸片
A
B
C
图1-1
A
B
C
图1-1
A
B
C
图1-2
6
8
x
5
x
13
PAGE
1
一、教学目的:
1、知识目标:
掌握勾股定理,了解利用拼图验证勾股定理的方法,会初步运用勾股定理进
行简单的计算和实际应用。
2、能力目标:
通过勾股定理的学习,使学生再次体会由特殊到一般,由具体到抽象的认识规律,培养学生推理、发现、分析动手及解决实际问题的能力。
3、情感目标:
通过勾股定理的教学,介绍我国古代人民在勾股定理研究方面的成就,激发学生的爱国热情。
二、教学重点
对勾股定理的理解和实际应用。
三、教学难点
在勾股定理的探索和验证过程中,进一步体会数形结合思想。
四、教具准备
多媒体课件
五、教学过程
导入新课
2002年在北京召开的国际数学大会上,到处可以看到这个简洁优美的图案(如图),这个远看像旋转的风车的图案是采用了1700多年前中国数学家赵爽用来证明勾股定理的弦图。
作为国际数学大会的会标,它为什么有如此大的魅力呢?它蕴含着怎样的奥妙呢?这节课就带领大家一起探索勾股定理。
推进新课
新知探求
1.观察归纳
(1)观察图1-1
正方形A中含有 个小方格,即A的面积是 个单位面积。
正方形B的面积是 个单位面积。
正方形C的面积是 个单位面积。
你是怎样得到正方形c 的面积?
(2)在图1-2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?
(3)你能发现图1-1中三个正方形A,B,C的面积之间有什么关系吗?图1-2中呢?
A的面积+B的面积=C的面积
即:两条直角边上的正方形面积之和等于斜边上的正方形的面积
问题:(1)你能用三角形的边长表示正方形的面积吗?
(2)你能发现直角三角形三边长度之间存在什么关系吗?与同伴进行交流。
直角三角形两直角边的平方和等于斜边的平方
2.实践验证
分别以5厘米、12厘米为直角边作出一个直角三角形,并测量斜边的长度。
(2)中的规律对这个三角形仍然成立吗?
3.总结
勾股定理(gou-gu theorem)
如果直角三角形两直角边分别为a、b,斜边为c,那么
a+b=c
即:直角三角形两直角边的平方和等于斜边的平方。
4.结论变形
直角三角形中,两直角边的平方和等于斜边的平方;
那么a+b=c 也就有:
应用示例
例1:如图:将长为5.41米的梯子AC斜靠在墙上,BC长为2.16米,求梯子上端A到墙的底边的垂直距离AB.(精确到0.01米)
图14.1.4
解 如图14.1.4,在Rt△ABC中,
BC=2.16米, AC=5.41米,
根据勾股定理可得
AB==≈4.96(米).
答: 梯子上端A到墙的底边的垂直距离 AB 约为4.96米.
例2:小明妈妈买了一部29英寸(74厘米)的电视机,小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗?
随堂练习
求出下列直角三角形中未知边的长度
小结
1、利用数格子的方法,探索了以直角三角形三边为边长的正方形面积的关系(即两个小正方形的面积之和等于大正方形的面积)
2、探索了直角三角形的三边关系,得到勾股定理:
即直角三角形两直角边的平方和等于斜边的平方
注意:应用勾股定理时应特别注意哪个角是直角。
作业
1. P55 第 2题
2.在直角三角形ABC中, ∠C=90°,
(1)已知: a=5, b=12, 求c;
(2)已知: b=6,c=10 , 求a;
3.准备四张形状相同大小一样的直角三角形硬纸片
A
B
C
图1-1
A
B
C
图1-1
A
B
C
图1-2
6
8
x
5
x
13
PAGE
1
