离散型随机变量的分布列

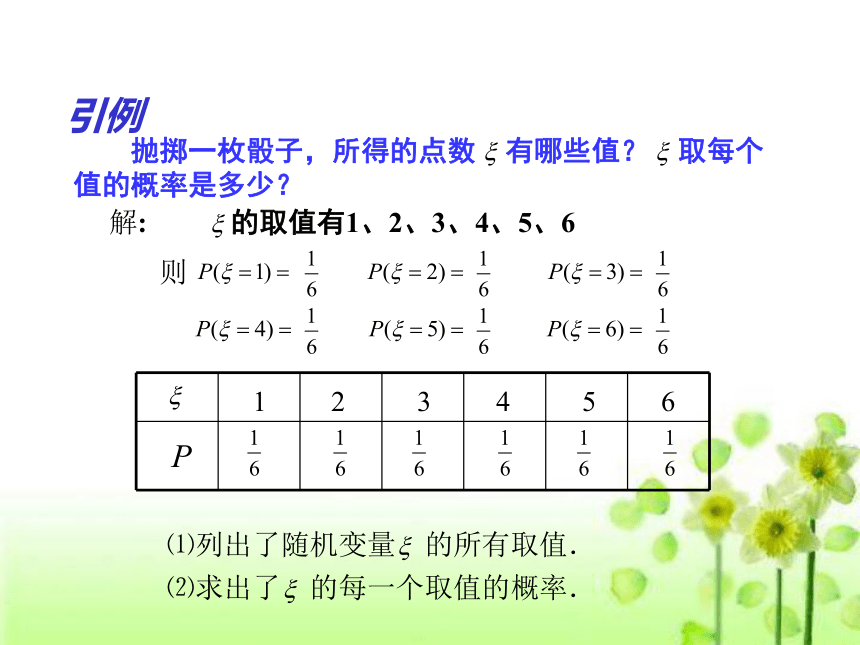
课件10张PPT。离散型随机变量的分布列（二）引例 　　抛掷一枚骰子，所得的点数　有哪些值？　取每个值的概率是多少？ 解:则⑵求出了　的每一个取值的概率．⑴列出了随机变量　的所有取值．　的取值有1、2、3、4、5、6二、离散型随机变量的分布列设随机变量　的所有可能的取值为则称表格的每一个取值　　　　　的概率为　　　　　，注:1、分布列的构成
2、分布列的性质返回　一袋中装有6个同样大小的小球，编号为1、2、3、4、5、6，现从中随机取出3个小球，以　表示取出球的最大号码，求　的分布列．例2：解:表示其中一个球号码等于“3”，另两个都比“3”小∴∴∴∴的所有取值为：3、4、5、6．表示其中一个球号码等于“4”，另两个都比“4”小表示其中一个球号码等于“5”，另两个都比“5”小表示其中一个球号码等于“3”，另两个都比“3”小返回例3：已知随机变量　的分布列如下：－2－13210分别求出随机变量⑴；⑵的分布列．解：且相应取值的概率没有变化返回例3：已知随机变量　的分布列如下：－2－13210分别求出随机变量⑴；⑵的分布列．解：返回课堂练习：1、某厂生产电子元件，其产品的次品率为5%，现从一批产品中任意地连续取出2件，求其中的次品数　的分布列．3、设随机变量　的分布列为则　的值为　　　　　．2、设随机变量　的分布列如下：4321则　的值为　　　　．课外作业：习题2．1　第5、6题