13章整式乘除的复习
图片预览






文档简介
课件17张PPT。 13章整式乘除的复习 民族实验中学1、幂的运算:(1)同底数的幂相乘,底数______,指数_________,
am · an=am+n(m,n为正整数)(2)幂的乘方,底数_____,指数_______(am)n=amn (m、n为正整数) (3)积的的乘方,等于________,(ab)n=an·bn(n为正整数) (4)同底数的幂相除,底数________,指数______
am÷an=am-n(a≠0, m,n为正整数,并且m>n) x2 · x7=_____;a2m ·a2n=________(y2)3=________;(b2)2n=________(3a2)2=________;(3p2q)3=_______复习应知应会同底数幂的除法:整式的运算(复习)1、幂的运算同底数幂的乘法:幂的乘方:积的乘方:2、整式的乘法:(1)单项式乘以单项式计算法则(2)单项式乘以多项式的计算法则m(a+b)=______(3)多项式乘以多项式计算法则(a+b)(m+n)=________ (4)乘法公式:
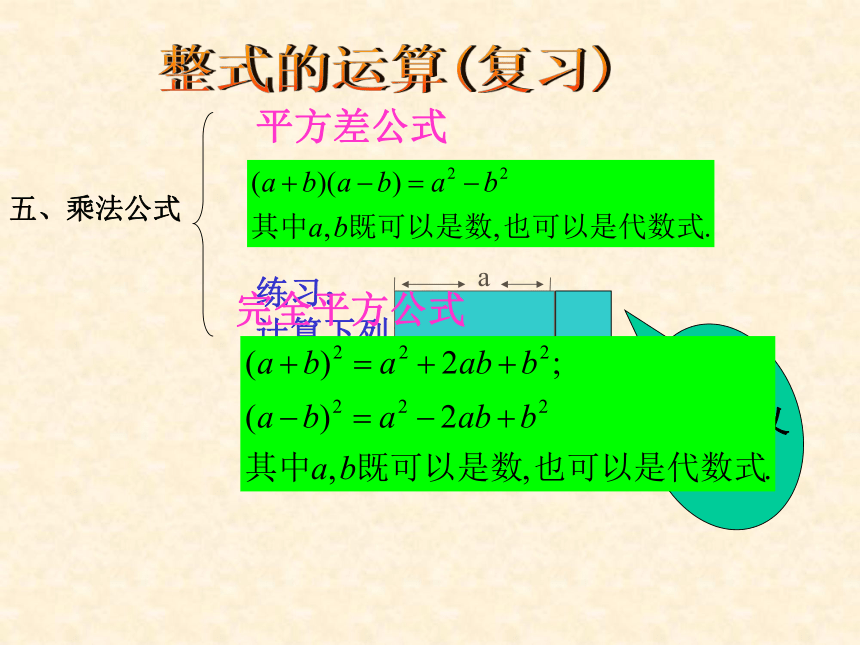
平方差公式:(a+b)(a-b)=________
完全平方公式:(a+b)2=_________;(a-b)2=________. (x+2)(y+3)=________(2x3y) · (3x2y3z)=________(-3a2)(2a3+a2 -1)=_______复习应知应会整式的运算(复习)四、整式的乘法单项式乘以单项式练习:(-3ab)·(-4b2)单项式乘以多项式练习:-6x(x-3y)多项式乘以多项式练习:(1) (2x+y)(x-y)
(2) (a+b+c)2整式的运算(复习)五、乘法公式平方差公式练习:
计算下列各式:
1、(5-6x)(5+6x)
2、(-m+n)(-m-n)完全平方公式图2练习:1、判断下列式子是否正确,
并说明理由。3、整式的除法:(1)单项式除以单项式计算法则(2)多项式除以多项式的计算法则(am+bm+cm) ÷m=___(-2x3)4y ÷x6=________复习应知应会(12a5b6c2-6b5c4) ÷(-2b2c)2 =_______4、因式分解:(1)因式分解的定义(2)因式分解的基本方法:(3)因式分解的步骤: ①_________;②_______________①_______;②_________;③__________;④____________复习应知应会探 索一一、幂的运算法则的正逆运用:1、m6·m6=ma ,则a=________2、(-x)9÷(-x)6÷(-x)÷x=_______ 3、若am=2,an=5,则am+n =__________ 4、已知n是正整数,且x2n=2,求(3x3n)2的值5、(0.5)2004×(-2)2005=________探 索二二、逆向思维、灵活运用乘法公式求值2、已知(x+y)2=1,(x-y)2=49,求x2+y2
与xy的值1、若x2-4y2=-15,x+2y=3,求x、y的值3、若多项式x2﹣5x+m分解因式的结
果为(x﹣3)(x+n),那么 m 、 n的值
分别是m_____,n=______
1、 计算:(a-1)(a4+1)(a2+1)(a+1)2、 计算:(2a-b)2(b+2a)2 二、创新思维探 索二3. 己知x+y=3 ,x2+y2=5 则xy 的值等于多少?4. 己知x-y=4 , xy=21 ,则 x2+y2 的值等于多少?
探索三三、转化思想与逆向思维1、 (x+1)(x2+mx+n) 的计算结果不含x2
和x项。反思拓展1、若x2n=5,求(3x3n)2﹣ 4(x2)2n的值。
2、已知4x=23x﹣1,求x的值。
3、已知a+b=5,ab=6,求a2+b2,a4+b4的值。
4、如果(x-3)是多项式(x2+4x+m)的一个
因式,求m的值。
5、若x2+y2-2x+6y+10=0,求x+y的值。感谢各位领导老师莅临指导
am · an=am+n(m,n为正整数)(2)幂的乘方,底数_____,指数_______(am)n=amn (m、n为正整数) (3)积的的乘方,等于________,(ab)n=an·bn(n为正整数) (4)同底数的幂相除,底数________,指数______
am÷an=am-n(a≠0, m,n为正整数,并且m>n) x2 · x7=_____;a2m ·a2n=________(y2)3=________;(b2)2n=________(3a2)2=________;(3p2q)3=_______复习应知应会同底数幂的除法:整式的运算(复习)1、幂的运算同底数幂的乘法:幂的乘方:积的乘方:2、整式的乘法:(1)单项式乘以单项式计算法则(2)单项式乘以多项式的计算法则m(a+b)=______(3)多项式乘以多项式计算法则(a+b)(m+n)=________ (4)乘法公式:
平方差公式:(a+b)(a-b)=________
完全平方公式:(a+b)2=_________;(a-b)2=________. (x+2)(y+3)=________(2x3y) · (3x2y3z)=________(-3a2)(2a3+a2 -1)=_______复习应知应会整式的运算(复习)四、整式的乘法单项式乘以单项式练习:(-3ab)·(-4b2)单项式乘以多项式练习:-6x(x-3y)多项式乘以多项式练习:(1) (2x+y)(x-y)
(2) (a+b+c)2整式的运算(复习)五、乘法公式平方差公式练习:
计算下列各式:
1、(5-6x)(5+6x)
2、(-m+n)(-m-n)完全平方公式图2练习:1、判断下列式子是否正确,
并说明理由。3、整式的除法:(1)单项式除以单项式计算法则(2)多项式除以多项式的计算法则(am+bm+cm) ÷m=___(-2x3)4y ÷x6=________复习应知应会(12a5b6c2-6b5c4) ÷(-2b2c)2 =_______4、因式分解:(1)因式分解的定义(2)因式分解的基本方法:(3)因式分解的步骤: ①_________;②_______________①_______;②_________;③__________;④____________复习应知应会探 索一一、幂的运算法则的正逆运用:1、m6·m6=ma ,则a=________2、(-x)9÷(-x)6÷(-x)÷x=_______ 3、若am=2,an=5,则am+n =__________ 4、已知n是正整数,且x2n=2,求(3x3n)2的值5、(0.5)2004×(-2)2005=________探 索二二、逆向思维、灵活运用乘法公式求值2、已知(x+y)2=1,(x-y)2=49,求x2+y2
与xy的值1、若x2-4y2=-15,x+2y=3,求x、y的值3、若多项式x2﹣5x+m分解因式的结
果为(x﹣3)(x+n),那么 m 、 n的值
分别是m_____,n=______
1、 计算:(a-1)(a4+1)(a2+1)(a+1)2、 计算:(2a-b)2(b+2a)2 二、创新思维探 索二3. 己知x+y=3 ,x2+y2=5 则xy 的值等于多少?4. 己知x-y=4 , xy=21 ,则 x2+y2 的值等于多少?
探索三三、转化思想与逆向思维1、 (x+1)(x2+mx+n) 的计算结果不含x2
和x项。反思拓展1、若x2n=5,求(3x3n)2﹣ 4(x2)2n的值。
2、已知4x=23x﹣1,求x的值。
3、已知a+b=5,ab=6,求a2+b2,a4+b4的值。
4、如果(x-3)是多项式(x2+4x+m)的一个
因式,求m的值。
5、若x2+y2-2x+6y+10=0,求x+y的值。感谢各位领导老师莅临指导
