探索三角形全等的条件（1）

课件33张PPT。
5.3 探索三角形全等的条件(1)问题引入:1.什么叫三角形？一个三角形有几条边？几个角？ 2.什么叫全等三角形？全等三角形有何性质？三条线段首尾顺次连接而成的图形;三条边,三个角.
能够完全重合的三角形.全等三角形的对应边相等，
对应角相等。
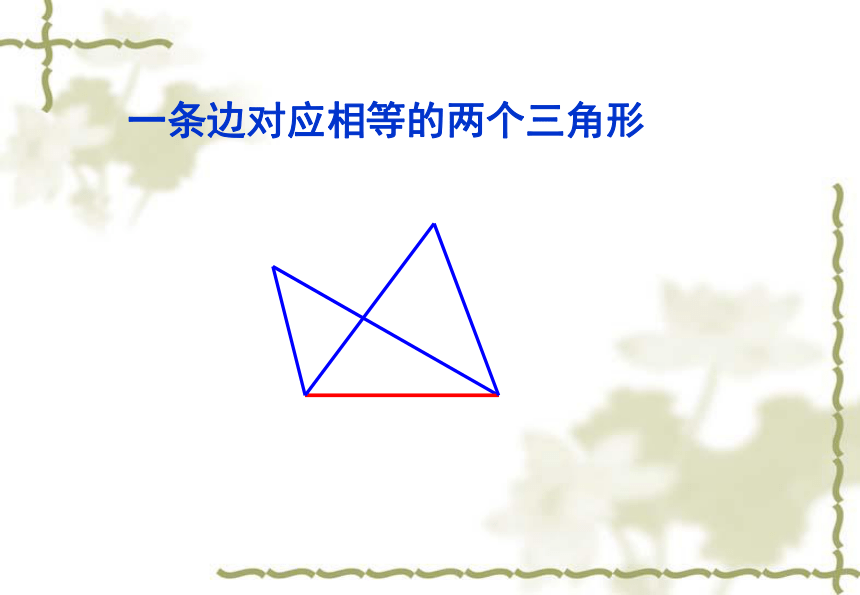
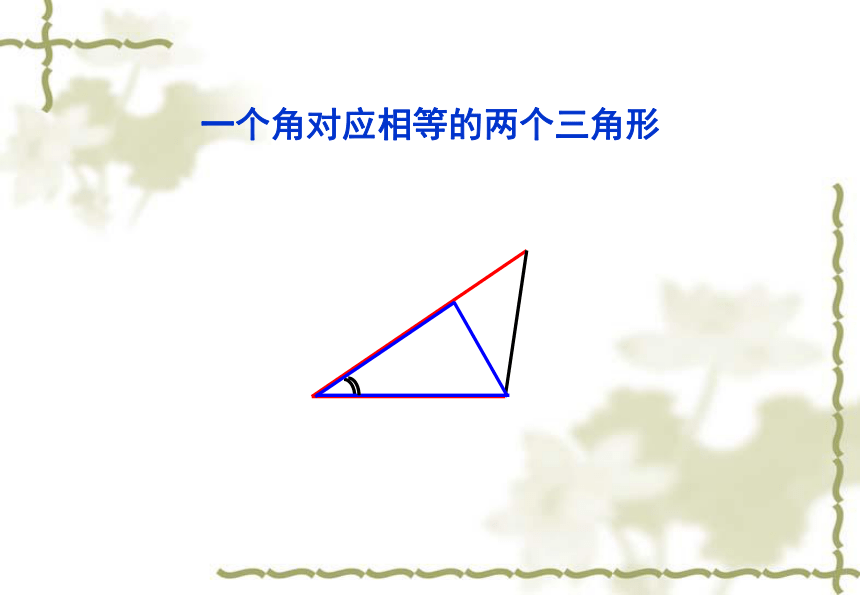
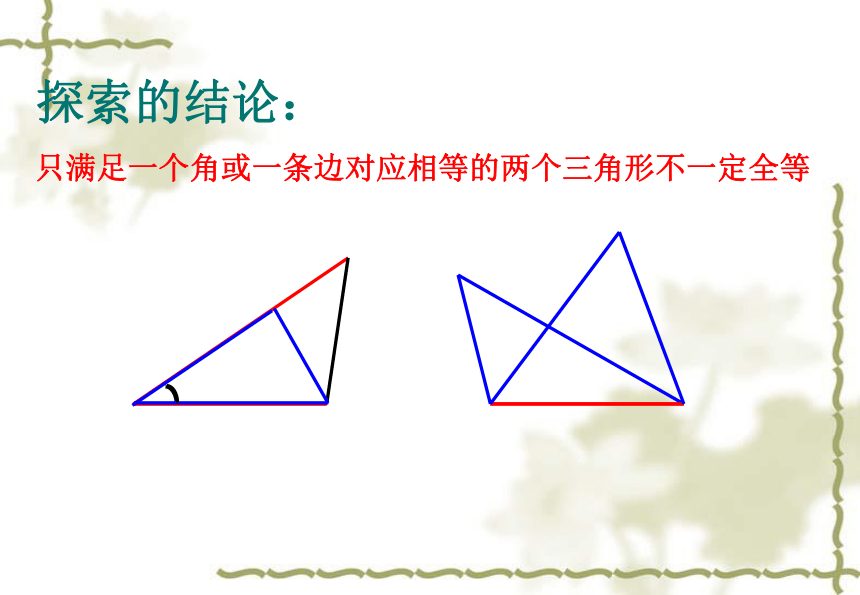
即两个全等三角形是完全一样的三角形。 想一想：要画一个三角形与小明画的三角形全等。需要几个与边或角的大小有关的条件？只知道一个条件（一角或一边）行吗？两个条件呢？三个条件呢？让我们一起来探索三角形全等的条件智者探宝 1：只给一个条件画三角形这一个条件可能为:一条边一个角一条边对应相等的两个三角形一个角对应相等的两个三角形探索的结论：只满足一个角或一条边对应相等的两个三角形不一定全等只给两个条件画三角形智者探宝 2 :(1)两条边
(2)两个角
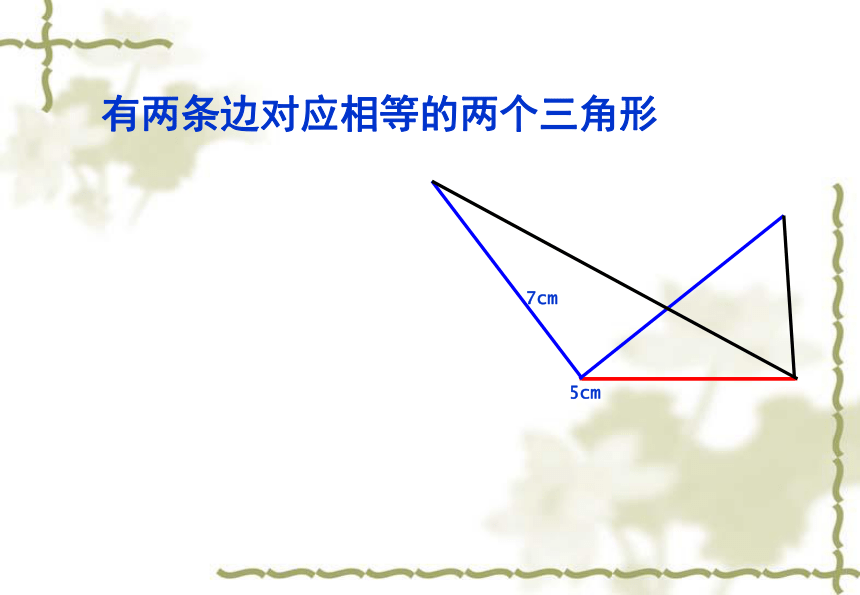
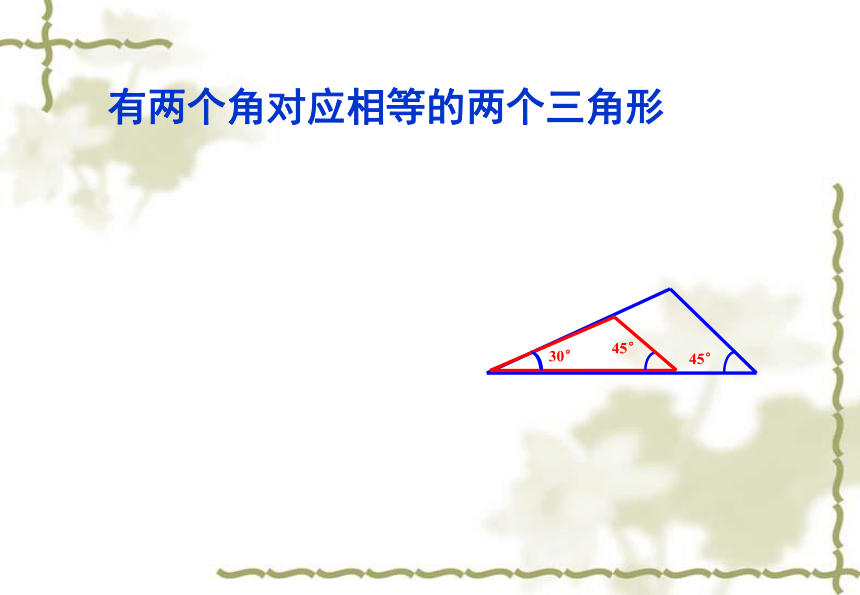
(3)一条边和一个角2.有两个角分别为30°,45°
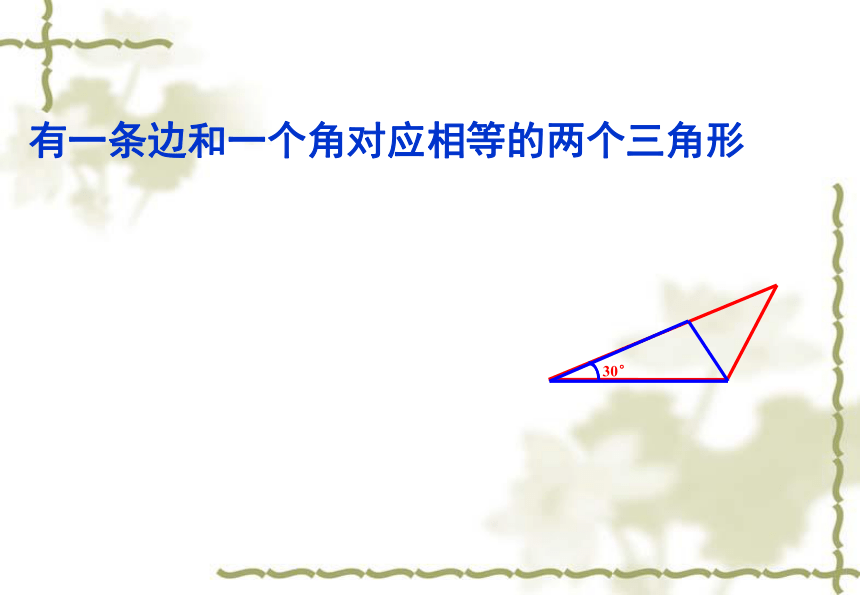
1.有两条边分别为5cm,7cm3.有一个角30°,一条边长为6cm有两条边对应相等的两个三角形有两个角对应相等的两个三角形有一条边和一个角对应相等的两个三角形探索的结论：只满足两条边或两个角或一条边和一个角对应相等的两个三角形不一定全等45°智者探宝 3： (1)三个角给出三个条件画三角形(2)三条边(3)两角一边(4)两边一角有三个角对应相等的两个三角形
请同学们以4cm、5cm、7cm为边画三角形合作探究 各显其能有三条边对应相等的两个三角形结论:三边对应相等的两个三角形全等简写为”边边边”或”SSS”因为AB=DE BC=EF CA=FD
所以△ABC≌ △DEF由此得出定理：三边对应相等的两个三角形全等，简写为“边边边”或“SSS”这个定理说明，只要三角形的三边的长度确定了，这个三角形的形状和大小就完全确定了，这也是三角形具有稳定性的原理。　由P158页介绍三角形稳定性的例子。下面的三角形中有哪几对全等三角形1、如图，AB=DC，AC=DB，△ABC和△DCB是否全等？试说明理由。 擂台争霸解：
AB=DC
AC=DB
BC=CB
△ABC≌△DCB在△ABC≌△DCB中，2、如图，AB=DF，AC=DE，BE=CF △ABC和△DEF是否全等？试说明理由。 擂台争霸变式练习3、如图，E、C是线段BF上的两点，AB=DF，AC=DE，要使△ABC和△DFE 根据“SSS”全等，还需要条件：
变式练习三组全等的三角形
△ABD≌ △ACD
△BDH≌ △CDH
△ABH≌ △ACH 四边形不具有稳定性，你有办法让它们稳定吗？ 挑战自我: 小明有一块“飞镖”，想知道∠B和∠C是否相等，但他没有量角器，只有一把刻度尺.
你能帮小明想个办法吗？智力检测:课后活动与探究:一个六边形钢架ABCDEF,由6条钢管连接而成（如图所示），为使这一钢架稳固，请你用三条钢管连接使它不能活动，你能找出几种方法？
练习：1、如图，AB＝AC，BD＝CD，BH＝CH，图中有几组全等的三角形？它们全等的条件是什么？HDCBA解：有三组。　　　　　　　　在△ABH和△ACH中 ∵AB=AC，BH=CH，AH=AH　∴△ABH≌△ACH（SSS）；在△ABD和△ACD中
∵AB=AC，BD=CD，AD=AD　∴△ABD≌△ACD（SSS）； 　在△DBH和△DCH中∵BD=CD，BH=CH，DH=DH∴△DBH≌△DCH（SSS）　练习2。如图，已知AB=CD，BC=DA。你能说明△ABC与△CDA全等吗？你能说明AB∥CD，AD∥BC吗？为什么？　DBAC解：在△ABC与△CDA中，
∵∴△ABC≌△CDA（SSS）
∴∠BAC=∠DCA,∠ACB=∠CAD(全等三角形对应角相等）　∴AB∥CD，AD∥BC（内错角相等，两直线平行）感悟与反思:通过本节课的探索学习，你有哪些收获？1: 两个三角形全等的条件：
“三边对应相等的两个三角形全等”。简称“边边边”或“SSS”。
2:三角形三边的长度确定,三角形的大小和形状就确定。
3：三角形具有稳定性