全等三角形的判定SAS
图片预览



文档简介
课件19张PPT。全等三角形的判定(一)——边角边雁江区丹山镇裕通中学 彭明刚ABCA'B'
C'
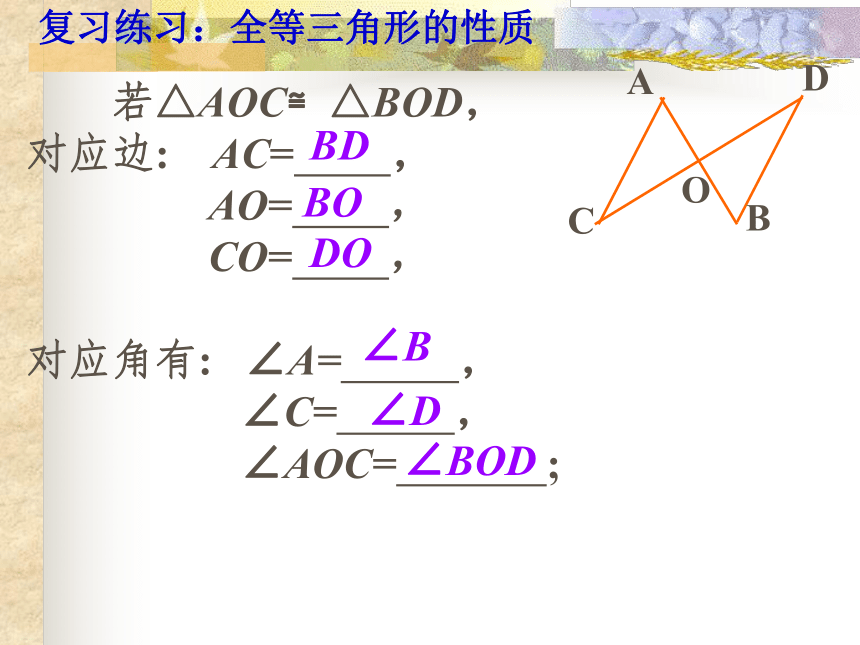
若△AOC≌△BOD,
对应边: AC= ,
AO= ,
CO= ,
对应角有: ∠A= ,
∠C= ,
∠AOC= ;
复习练习:全等三角形的性质BDBODO∠B∠D∠BOD引入新课思 考
如果两个三角形有三组对应相等的元素(边或角),那么会有哪几种可能的情况?这时,这两个三角形一定会全等吗?
?
上节课我们留给大家了这样一个思考题,你们思考好了吗? 有以下的四种情况:
两边一角、两角一边、
三角、三边.
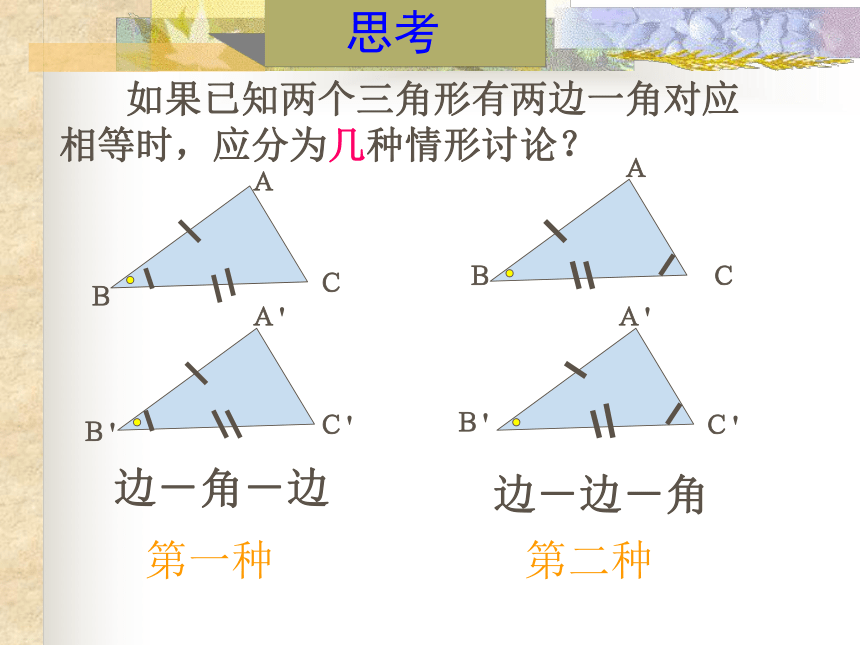
温馨提示要不重不漏哦 思考 如果已知两个三角形有两边一角对应相等时,应分为几种情形讨论?边-角-边边-边-角AAA'
A'BB'
BB'
CCC'
C'
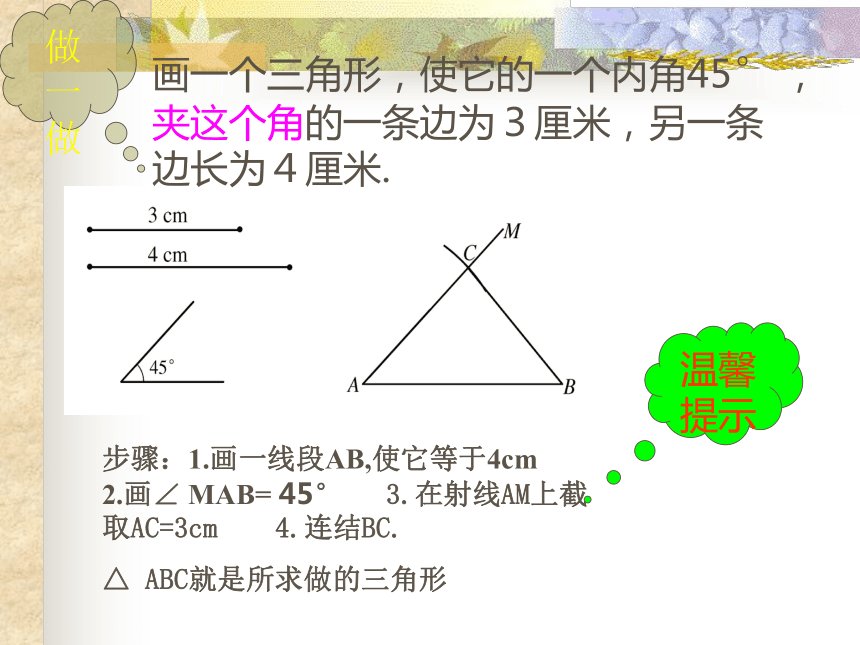
第一种第二种做一做画一个三角形,使它的一个内角45° ,夹这个角的一条边为3厘米,另一条边长为4厘米.
步骤:1.画一线段AB,使它等于4cm 2.画∠ MAB= 45° 3.在射线AM上截取AC=3cm 4.连结BC.
△ ABC就是所求做的三角形温馨提示
你画的三角形与同伴画的一定全等吗?实践检验全等同桌两个同学自行约定:各画一个三角形,使它们具有相同的两条线段和一个夹角,比较一下,可以得出什么结论?实践与探索在两个三角形中,如果有两条边及它们的夹角对应相等,那么这两个三角形全等(简记为S.A.S)
结论:
温馨提示:这是一个公理S.A.S的证明: 如图在△ABC和△A′B′C′中,已知AB=A′B′, ∠B=∠B′, BC=B′C′.
由于AB=A′B′,我们移动其中的△ABC,使点A与点A′、点B与点B′重合;因为∠B=∠B′,因此可以使∠B与∠B′的另一边BC与B′C′重叠在一起,而BC=B′C′,因此点C与点C′重合.于是△ABC与△A′B′C′重合,这就说明这两个三角形全等. 例1如图19.2.4,在△ABC中,AB=AC, AD平分∠BAC,求证: △ABD≌△ACD.
证明: ∵ AD平分∠BAC,
∴ ∠BAD=∠CAD.
在△ABD与△ACD中,
AB=AC,(已知)
∠BAD=∠CAD,(已证)
AD=AD,(公共边)
∴ △ABD≌△ACD(S.A.S.).
∵1: 如图,已知AB和CD相交与O, OA=OB, OC=OD.说明 △ OAD与
△ OBC全等的理由
∴△OAD≌△OBC (S.A.S) 解:在△OAD 和△OBC中巩固练习
巩固练习
2.?如图所示, 根据题目条件,判断下面的三角形是否全等.
(1) AC=DF, ∠C=∠F, BC=EF;
(2) BC=BD, ∠ABC=∠ABD.
答案:(1)全等(2)全等例2:小兰做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,将上述条件标注在图中,小明不用测量就能知道EH=FH吗?与同桌进行交流。解:在△EDH和△FDH中: ED=FD(已知)
∠EDH=∠FDH(已知)
DH=DH(公共边)∴△EDH≌△FDH(S.A.S)
∴EH=FH(全等三角形对应边相等)
巩固练习
3.点M是等腰梯形ABCD底边AB的中点,求证DM=CM,∠ADM=∠BCM.
证明:∵ 点M是等腰梯形ABCD底边AB的中点
∴ AD=BC (等腰梯形的两腰相等)
∠A=∠B(等腰梯形的两底角相等)
AM=BM (线段中点的定义)
在△ADM和△BCM中 AD=BC, (已证)
∠A=∠B, (已证)
AM=BM, (已证)
∴△AMD≌△BMC (S.A.S)∴ DM=CM(全等三角形的对应边相等)∠ADM=∠BCM (全等三角形的对应角相等)链接生活: 小明不小心打翻了墨水,将自己所画的三角形涂黑了,你能帮小明想想办法,画一个与原来完全一样的三角形吗?能B’∵ AB = A’B’ ∠B = ∠B’
BC =B’C’∴ △ ABC≌ △A’B’C’(S.A.S)ABCA’B’C’ 以3cm、4cm为三角形的两边,长度3cm的边所对的角为45° ,情况又怎样?动手画一画,你发现了什么?ABC3cm4cm45°3cm结论:两边及其一边所对的角相等,两个三角形不一定全等 做一做问题:那么边边角对应相等时情况又是怎样的呢?MB’ 步骤:1.画一线段AC,使它等于4cm 2.画∠ CAM= 45° 3.以C为圆心, 3cm长为半径画弧,交AM于点B 4.连结CB
△ ABC 就是所求做的三角形 显然: △ ABC与△ AB’C不全等和B’、CB’与△ AB’C1、今天我们学习了哪种方法判定两三角形全等?答:S.A.S 通过证明三角形全等可以证明两条线段等、两个角相等2、 “边边角”能不能判定两个三角形全等“?说一说今天你学到了什么答:不能作业P79习题19.2 第 2、4题
P96复习题 第4题谢谢!再见
C'
若△AOC≌△BOD,
对应边: AC= ,
AO= ,
CO= ,
对应角有: ∠A= ,
∠C= ,
∠AOC= ;
复习练习:全等三角形的性质BDBODO∠B∠D∠BOD引入新课思 考
如果两个三角形有三组对应相等的元素(边或角),那么会有哪几种可能的情况?这时,这两个三角形一定会全等吗?
?
上节课我们留给大家了这样一个思考题,你们思考好了吗? 有以下的四种情况:
两边一角、两角一边、
三角、三边.
温馨提示要不重不漏哦 思考 如果已知两个三角形有两边一角对应相等时,应分为几种情形讨论?边-角-边边-边-角AAA'
A'BB'
BB'
CCC'
C'
第一种第二种做一做画一个三角形,使它的一个内角45° ,夹这个角的一条边为3厘米,另一条边长为4厘米.
步骤:1.画一线段AB,使它等于4cm 2.画∠ MAB= 45° 3.在射线AM上截取AC=3cm 4.连结BC.
△ ABC就是所求做的三角形温馨提示
你画的三角形与同伴画的一定全等吗?实践检验全等同桌两个同学自行约定:各画一个三角形,使它们具有相同的两条线段和一个夹角,比较一下,可以得出什么结论?实践与探索在两个三角形中,如果有两条边及它们的夹角对应相等,那么这两个三角形全等(简记为S.A.S)
结论:
温馨提示:这是一个公理S.A.S的证明: 如图在△ABC和△A′B′C′中,已知AB=A′B′, ∠B=∠B′, BC=B′C′.
由于AB=A′B′,我们移动其中的△ABC,使点A与点A′、点B与点B′重合;因为∠B=∠B′,因此可以使∠B与∠B′的另一边BC与B′C′重叠在一起,而BC=B′C′,因此点C与点C′重合.于是△ABC与△A′B′C′重合,这就说明这两个三角形全等. 例1如图19.2.4,在△ABC中,AB=AC, AD平分∠BAC,求证: △ABD≌△ACD.
证明: ∵ AD平分∠BAC,
∴ ∠BAD=∠CAD.
在△ABD与△ACD中,
AB=AC,(已知)
∠BAD=∠CAD,(已证)
AD=AD,(公共边)
∴ △ABD≌△ACD(S.A.S.).
∵1: 如图,已知AB和CD相交与O, OA=OB, OC=OD.说明 △ OAD与
△ OBC全等的理由
∴△OAD≌△OBC (S.A.S) 解:在△OAD 和△OBC中巩固练习
巩固练习
2.?如图所示, 根据题目条件,判断下面的三角形是否全等.
(1) AC=DF, ∠C=∠F, BC=EF;
(2) BC=BD, ∠ABC=∠ABD.
答案:(1)全等(2)全等例2:小兰做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,将上述条件标注在图中,小明不用测量就能知道EH=FH吗?与同桌进行交流。解:在△EDH和△FDH中: ED=FD(已知)
∠EDH=∠FDH(已知)
DH=DH(公共边)∴△EDH≌△FDH(S.A.S)
∴EH=FH(全等三角形对应边相等)
巩固练习
3.点M是等腰梯形ABCD底边AB的中点,求证DM=CM,∠ADM=∠BCM.
证明:∵ 点M是等腰梯形ABCD底边AB的中点
∴ AD=BC (等腰梯形的两腰相等)
∠A=∠B(等腰梯形的两底角相等)
AM=BM (线段中点的定义)
在△ADM和△BCM中 AD=BC, (已证)
∠A=∠B, (已证)
AM=BM, (已证)
∴△AMD≌△BMC (S.A.S)∴ DM=CM(全等三角形的对应边相等)∠ADM=∠BCM (全等三角形的对应角相等)链接生活: 小明不小心打翻了墨水,将自己所画的三角形涂黑了,你能帮小明想想办法,画一个与原来完全一样的三角形吗?能B’∵ AB = A’B’ ∠B = ∠B’
BC =B’C’∴ △ ABC≌ △A’B’C’(S.A.S)ABCA’B’C’ 以3cm、4cm为三角形的两边,长度3cm的边所对的角为45° ,情况又怎样?动手画一画,你发现了什么?ABC3cm4cm45°3cm结论:两边及其一边所对的角相等,两个三角形不一定全等 做一做问题:那么边边角对应相等时情况又是怎样的呢?MB’ 步骤:1.画一线段AC,使它等于4cm 2.画∠ CAM= 45° 3.以C为圆心, 3cm长为半径画弧,交AM于点B 4.连结CB
△ ABC 就是所求做的三角形 显然: △ ABC与△ AB’C不全等和B’、CB’与△ AB’C1、今天我们学习了哪种方法判定两三角形全等?答:S.A.S 通过证明三角形全等可以证明两条线段等、两个角相等2、 “边边角”能不能判定两个三角形全等“?说一说今天你学到了什么答:不能作业P79习题19.2 第 2、4题
P96复习题 第4题谢谢!再见
