平方根第一课时

课件24张PPT。平方根制作人：王相卜1、我们已经学习过哪些运算？它们中互为逆运算的是？ 答：加法、减法、乘法、除法、乘方五种运算。加法与减法互逆；乘法与除法互逆。2、乘方有没有逆运算？7米7米？100米2？（图一）（图二）（1）图一的正方形的面积为＿＿＿＿＿；
（2）图二的正方形的边长为＿＿＿＿＿；
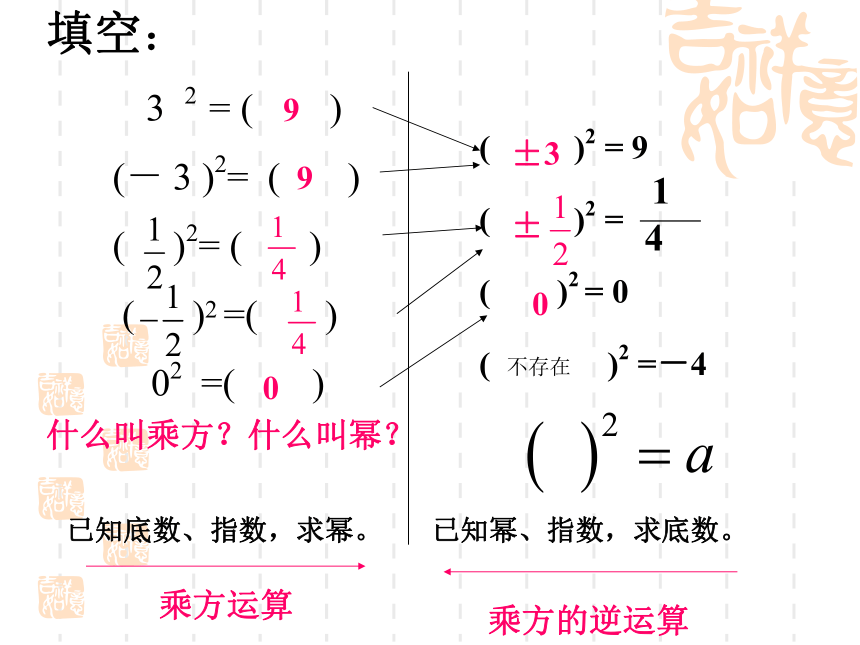
49米210米（3）除了10以外还有什么数的平方也是100吗？已知底数、指数，求幂。已知幂、指数，求底数。填空：
3 2 = ( )
(－ 3 )2= ( )
( )2= ( )
( )2 =( )
02 =( )990±30什么叫乘方？什么叫幂？不存在x是a的平方根。X2 = a一般地,如果一个数的平方等于a,那么这个数叫做a的平方根，也叫做a的二次方根。平方根的表示方法、读法被开方数开平方：
求一个数a(a≥0)的平方根的运算，叫做开平方，开平方运算是已知指数和幂，求底数。9的平方根：9的正的平方根：9的负的平方根：表示25的正的平方根。表示7的平方根。例1：求下列各数的平方根：
（1）81；（2） ；（3）2 ；（4）0.49 解：(1) ∵(±9)2=81 ∴81的平方根是±9；即 思考：是不是所有的数都能进行开平方运算 ？不是，只有正数和零才能进行开平方运算。 得出：( )2 = 9
( )2 =
( )2 = 0
( )2 =－4
3 2 = ( )
(－3 )2= ( )
( )2= ( )
( )2 =( )
02 =( )990±30不存在请同学们概括一个数的平方根的性质： ★一个正数有两个平方根，它们互为相反数；
★零有一个平方根，它是零本身；
★负数没有平方根。
例2：下列各数有平方根吗？如果有，求出它的平方根，如果没有，说明理由。
(1)-64 (2) 0 (3) (-4)2 (4) 10-2
1、检验下面各题中前面的数是不是后面的数的平方根。
（1）±12 , 144 （2）±0.2 , 0.04
（3）102 ，104 （4）14 ，256
2、选择题 （1） 0.01的平方根是 （ ）
（A）0.1 （B）±0.1 （C）0.0001 （D）±0.0001
（2）∵ （0.3）2 = 0.09 ∴ （ ）
（A）0.09 是 0.3的平方根. （B）0.09是0.3的3倍.
（C）0.3 是0.09 的平方根. （D）0.3不是0.09的平方根.
是是是不是BC练习2：
判断下列说法是否正确：
（1）－9的平方根是－3; ( )
（2）49的平方根是7 ； ( )
（3）（－2）2的平方根是±2 ；（ ）
（4）－1 是 1的平方根; （ ）
（5）若X2 = 16 则X = 4 （ ）
（6）7的平方根是±49. ( )××√√××负数没有平方根定义：求一个数的平方根的运算，叫做开平方。小 结当a=0时，a的平方根是0。
判断下列各数有没有平方根，若有，求其平方根。若没有，说明为什么。
（1） 0.81 （2） （3） －100 （4） （－4）2
（5）0 （6） （7） 10（3）∵ －100 是负数，∴ －100 没有平方根；解：（2）（1）（4）（6）（7）（5）0的平方根是0。 1、对于代数式3m-9，当m取何值时，（1）有两个平方根，并且它们互为相反数？（2）只有一个平方根？（3）没有平方根？
2、√x-2 是 x-2 的平方根,则x
3、一个正数的正的平方根是m，那么比这个正数大1的数的平方根是（ ）
A、m2+1；B、±√m+1；C、√m2+1；
D、±√m2+1思考题：算术平方根的完整定义
正数a的正的平方根叫做a的算术平方根，0的平方根也叫做0的算术平方根。（5）(－4)2的算术平方根是（4）10的算术平方根是（3）0.01的算术平方根是（2）9的算术平方根是（1）9的算术平方根是探索 和 交流（6）算术平方根等于它本身的是30.140或1计算：1.本节课引入了新的运算------开方运算，开方和乘方互为逆运算，从而完备了初等代数中六种基本代数运算（加、减、乘、除、乘方、开方），这对代数内容学习有着重要的意义。2.本节主要学习了:①平方根的概念； ②平方根的性质：一个正数有两个平方根，它们互为相反数，0的平方根是0，负数没有平方根；③平方根的表示方法；④求一个数的平方根的运算—开平方，应分清平方运算与开平方运算的区别与联系.
3.算术平方根的定义及表示方法小结 和 归纳观察右图,每个小正方形的边长均为1,我们可以得到小正方形的面积为1. .
(1)图中阴影正方形的面积是多少?它的边长是多少?
(2)估计 2 的值在哪两个整数之间? .

再见!