1.4 正余弦函数的图像和性质(学案)
文档属性
| 名称 | 1.4 正余弦函数的图像和性质(学案) |
|
|
| 格式 | rar | ||
| 文件大小 | 138.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-11-23 00:00:00 | ||
图片预览


文档简介
曲靖市第二中学 第一章 三角函数 2010级高一数学备课组
1.4 正余弦函数的图像和性质
一、导学目标
1.理解并掌握利用单位圆作正弦函数和余弦函数图象的方法;
2.理解并熟练掌握用“五点法”作出正弦函数、余弦函数的简图的方法,并利用图象解决一些有关问题;
3.掌握正、余弦函数的周期和最小正周期,并能求出正、余弦函数的最小正周期;
4.掌握正、余弦函数的奇、偶性的判断,并能求出正、余弦函数的单调区间.
二、尝试练习
(一)知识探究
1.用单位圆中的正弦线、余弦线作正弦函数、余弦函数的图象
(几何法):为了作三角函数的图象,三角函数的自变量要用弧度制来度量,使自变量与函数值都为实数.
① 函数y=sinx的图象
第一步:在直角坐标系的轴上任取一点,以为圆心作单位圆,从这个圆与轴的交点A起把圆分成n(这里n=12)等份.把轴上从到这一段分成(这里)等份.
第二步:在单位圆中画出对应于角,,,…,的正弦线(等价于“列表” ).把角的正弦线向右平行移动,使得正弦线的起点与轴上相应的点重合,则正弦线的终点就是正弦函数图象上的点(等价于“描点” ).
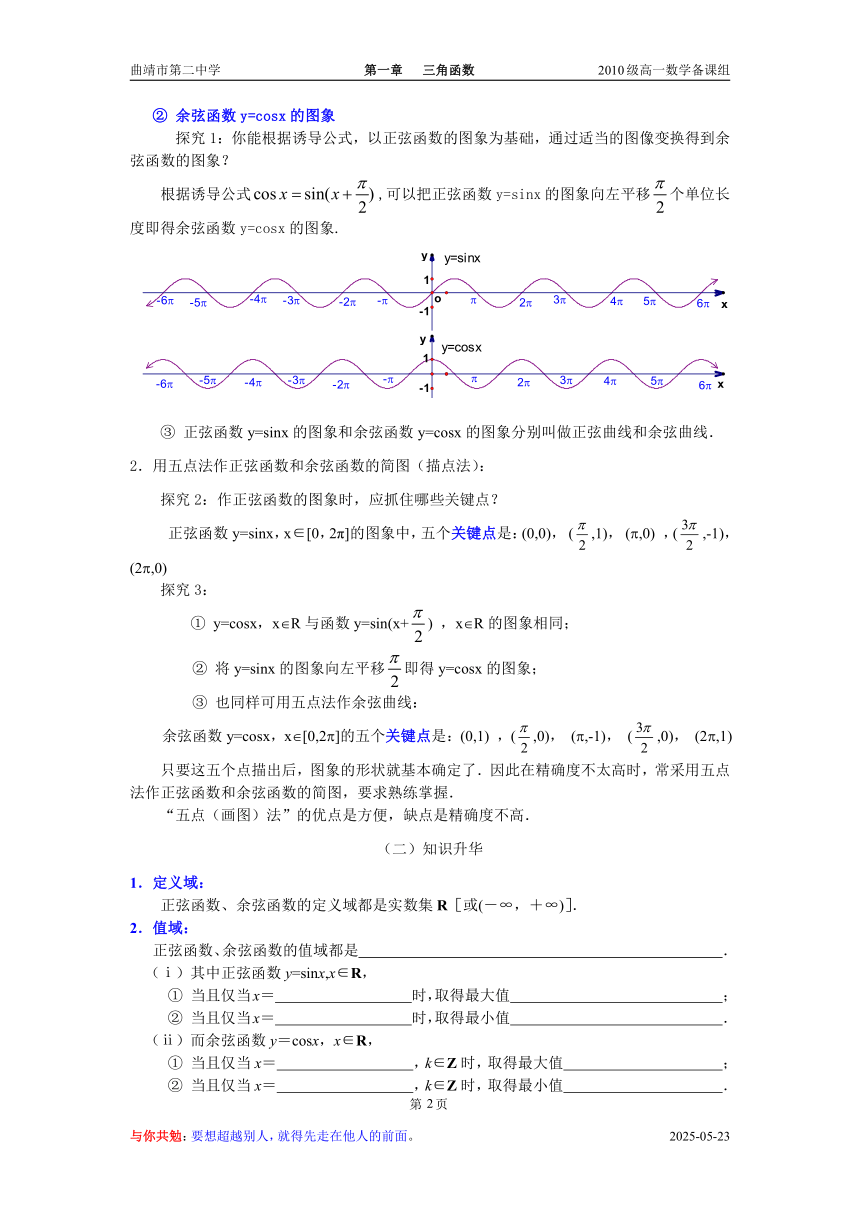
第三步:连线.用光滑曲线把这些正弦线的终点连结起来,就得到正弦函数y=sinx,x∈[0,2π]的图象.
根据终边相同的同名三角函数值相等,把上述图象沿着轴向右、向左连续地平行移动(每次移动个单位长度),就得到y=sinx,x∈R的图象.
把角的正弦线平行移动,使得正弦线的起点与轴上相应的点重合,则正弦线的终点的轨迹就是正弦函数y=sinx的图象.
② 余弦函数y=cosx的图象
探究1:你能根据诱导公式,以正弦函数的图象为基础,通过适当的图像变换得到余弦函数的图象?
根据诱导公式,可以把正弦函数y=sinx的图象向左平移个单位长度即得余弦函数y=cosx的图象.
③ 正弦函数y=sinx的图象和余弦函数y=cosx的图象分别叫做正弦曲线和余弦曲线.
2.用五点法作正弦函数和余弦函数的简图(描点法):
探究2:作正弦函数的图象时,应抓住哪些关键点?
正弦函数y=sinx,x∈[0,2π]的图象中,五个关键点是:(0,0), (,1), (,0) ,(,-1), (2,0)
探究3:
① y=cosx,xR与函数y=sin(x+) ,xR的图象相同;
② 将y=sinx的图象向左平移即得y=cosx的图象;
③ 也同样可用五点法作余弦曲线:
余弦函数y=cosx,x[0,2]的五个关键点是:(0,1) ,(,0), (,-1), (,0), (2,1)
只要这五个点描出后,图象的形状就基本确定了.因此在精确度不太高时,常采用五点法作正弦函数和余弦函数的简图,要求熟练掌握.
“五点(画图)法”的优点是方便,缺点是精确度不高.
(二)知识升华
1.定义域:
正弦函数、余弦函数的定义域都是实数集R[或(-∞,+∞)].
2.值域:
正弦函数、余弦函数的值域都是 .
(ⅰ)其中正弦函数y=sinx,x∈R,
① 当且仅当x= 时,取得最大值 ;
② 当且仅当x= 时,取得最小值 .
(ⅱ)而余弦函数y=cosx,x∈R,
① 当且仅当x= ,k∈Z时,取得最大值 ;
② 当且仅当x= ,k∈Z时,取得最小值 .
3.奇偶性:
(ⅰ)正弦曲线关于 对称,余弦曲线关于 对称,所以函数y=sinxx,x∈R为 函数,y=cosxx,x∈R为 函数.
(ⅱ)y=sinx的对称轴为x=,k∈Z, y=cosx的对称轴为x=,k∈Z;
y=sinx的对称中心为x=,k∈Z ,y=cosx的对称中心为x=,k∈Z.
4.单调性:
(ⅰ)正弦函数在每一个闭区间[-+2kπ,+2kπ](k∈Z)上都是增函数,其值从-1增大到1;在每一个闭区间[+2kπ,+2kπ](k∈Z)上都是减函数,其值从1减小到-1.
(ⅱ)余弦函数在每一个闭区间[(2k-1)π,2kπ](k∈Z)上都是增函数,其值从-1增加到1;在每一个闭区间[2kπ,(2k+1)π](k∈Z)上都是减函数,其值从1减小到-1.
5.周期性:
(ⅰ)(观察图象)正弦函数性质如下:
1 正弦函数的图象是有规律不断重复出现的;
2 规律是:每隔2重复出现一次(或者说每隔2k,kZ重复出现);
3 这个规律由诱导公式sin(2k+x)=sinx可以说明.
结论:象这样的函数叫做周期函数.
文字语言:正弦函数值按照一定的规律不断重复地取得。
符号语言:当增加()时,总有.
也即:(1)当自变量增加时,正弦函数的值又重复出现;
(2)对于定义域内的任意,恒成立.
余弦函数也具有同样的性质,这种性质我们就称之为函数的周期性.
(ⅱ) 周期函数定义:对于函数f (x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有:f (x+T)=f (x)那么函数f (x)就叫做周期函数,非零常数T叫做这个函数的周期.
问题:(1)对于函数,有,能否说是它的周期?
(2)正弦函数,是不是周期函数,如果是,周期是多少?
(3)若函数的周期为,则,也是的周期吗?为什么?
(是,其原因为:)
说明: (1)周期函数x定义域M,则必有x+TM, 且若T>0则定义域无上界;T<0则定义域无下界;
(2)“每一个值”只要有一个反例,则f (x)就不为周期函数(如f (x0+t)f (x0));
(3)T往往是多值的(如y=sinx,2,4,…,-2,-4,…都是周期)周期T中最小的正数叫做f (x)的最小正周期(有些周期函数没有最小正周期);
一般结论:函数及函数,的周期.
(三)我也能行
1.画出函数,的简图,并回答下列问题.
① 在上的解集为 .
② 在上的解集为 .
③ 在上的解为 .
2.求使函数取得最大值、最小值的自变量的集合,并分别写出最大值、最小值是什么.
3.(2010湖北—文2)函数 =,的最小正周期为 ( )
A. B. C. D.
4.(2006北京—文2)函数y=1+cosx的图象 ( )
A.关于x轴对称 B.关于y轴对称
C.关于原点对称 D.关于直线x=对称
5.函数的周期是 ,对称轴是 ,对称中心是 ,单调递增区间是 .
三、精点精评
【例1】 函数y=3sin(-2x)在什么区间是减函数?当时,求该函数的单调递减区间.
【例2】 函数y=|sinx|的周期是
【解析】 作出函数y=|sinx|的简图(如下图所示),由图可知函数的周期是.
四、直击高考
1.(2006辽宁—文1) 函数的最小正周期是( )
A ( http: / / wxc. / ) B ( http: / / wxc. / ) C ( http: / / wxc. / ) D ( http: / / wxc. / )
2.函数y=sin(2x+)图象的一条对称轴方程是 ( )
A.x=- B.x=- C.x= D.x=
3.(2007福建—文5)函数的图象 ( )
A ( http: / / wxc. ) 关于点对称 B ( http: / / wxc. ) 关于直线对称
C ( http: / / wxc. ) 关于点对称 D ( http: / / wxc. ) 关于直线对称
4.(2009浙江—理8)已知a是实数,则函数f(x)=1+asinax的图像不可能是 ( )
5.(2004天津—文10) 函数为增函数的区间是 ( )
A. B. C. D.
6.(2009四川—理4)已知函数,下面结论错误的是 ( )
A.函数的最小正周期为 B.函数在区间上是增函数
C.函数的图像关于直线对称 D.函数是奇函数
7.(2007全国II—文3)函数的一个单调增区间是 ( )
A. B. C. D.
8.(2006湖南—文3)设点P是函数的图象C的一个对称中心,若点P到图象C的对称轴上的距离的最小值,则的最小正周期是
A ( http: / / wxc. / ) 2π B ( http: / / wxc. / ) π C ( http: / / wxc. / ) D ( http: / / wxc. / )
9.(2008江苏1)最小正周期为,其中,则 10
心得与体会
-1
1
o
x
y
-
3
2
-1
1
o
x
y
PAGE
6
第 页
与你共勉:要想超越别人,就得先走在他人的前面。 2010-11-23
1.4 正余弦函数的图像和性质
一、导学目标
1.理解并掌握利用单位圆作正弦函数和余弦函数图象的方法;
2.理解并熟练掌握用“五点法”作出正弦函数、余弦函数的简图的方法,并利用图象解决一些有关问题;
3.掌握正、余弦函数的周期和最小正周期,并能求出正、余弦函数的最小正周期;
4.掌握正、余弦函数的奇、偶性的判断,并能求出正、余弦函数的单调区间.
二、尝试练习
(一)知识探究
1.用单位圆中的正弦线、余弦线作正弦函数、余弦函数的图象
(几何法):为了作三角函数的图象,三角函数的自变量要用弧度制来度量,使自变量与函数值都为实数.
① 函数y=sinx的图象
第一步:在直角坐标系的轴上任取一点,以为圆心作单位圆,从这个圆与轴的交点A起把圆分成n(这里n=12)等份.把轴上从到这一段分成(这里)等份.
第二步:在单位圆中画出对应于角,,,…,的正弦线(等价于“列表” ).把角的正弦线向右平行移动,使得正弦线的起点与轴上相应的点重合,则正弦线的终点就是正弦函数图象上的点(等价于“描点” ).
第三步:连线.用光滑曲线把这些正弦线的终点连结起来,就得到正弦函数y=sinx,x∈[0,2π]的图象.
根据终边相同的同名三角函数值相等,把上述图象沿着轴向右、向左连续地平行移动(每次移动个单位长度),就得到y=sinx,x∈R的图象.
把角的正弦线平行移动,使得正弦线的起点与轴上相应的点重合,则正弦线的终点的轨迹就是正弦函数y=sinx的图象.
② 余弦函数y=cosx的图象
探究1:你能根据诱导公式,以正弦函数的图象为基础,通过适当的图像变换得到余弦函数的图象?
根据诱导公式,可以把正弦函数y=sinx的图象向左平移个单位长度即得余弦函数y=cosx的图象.
③ 正弦函数y=sinx的图象和余弦函数y=cosx的图象分别叫做正弦曲线和余弦曲线.
2.用五点法作正弦函数和余弦函数的简图(描点法):
探究2:作正弦函数的图象时,应抓住哪些关键点?
正弦函数y=sinx,x∈[0,2π]的图象中,五个关键点是:(0,0), (,1), (,0) ,(,-1), (2,0)
探究3:
① y=cosx,xR与函数y=sin(x+) ,xR的图象相同;
② 将y=sinx的图象向左平移即得y=cosx的图象;
③ 也同样可用五点法作余弦曲线:
余弦函数y=cosx,x[0,2]的五个关键点是:(0,1) ,(,0), (,-1), (,0), (2,1)
只要这五个点描出后,图象的形状就基本确定了.因此在精确度不太高时,常采用五点法作正弦函数和余弦函数的简图,要求熟练掌握.
“五点(画图)法”的优点是方便,缺点是精确度不高.
(二)知识升华
1.定义域:
正弦函数、余弦函数的定义域都是实数集R[或(-∞,+∞)].
2.值域:
正弦函数、余弦函数的值域都是 .
(ⅰ)其中正弦函数y=sinx,x∈R,
① 当且仅当x= 时,取得最大值 ;
② 当且仅当x= 时,取得最小值 .
(ⅱ)而余弦函数y=cosx,x∈R,
① 当且仅当x= ,k∈Z时,取得最大值 ;
② 当且仅当x= ,k∈Z时,取得最小值 .
3.奇偶性:
(ⅰ)正弦曲线关于 对称,余弦曲线关于 对称,所以函数y=sinxx,x∈R为 函数,y=cosxx,x∈R为 函数.
(ⅱ)y=sinx的对称轴为x=,k∈Z, y=cosx的对称轴为x=,k∈Z;
y=sinx的对称中心为x=,k∈Z ,y=cosx的对称中心为x=,k∈Z.
4.单调性:
(ⅰ)正弦函数在每一个闭区间[-+2kπ,+2kπ](k∈Z)上都是增函数,其值从-1增大到1;在每一个闭区间[+2kπ,+2kπ](k∈Z)上都是减函数,其值从1减小到-1.
(ⅱ)余弦函数在每一个闭区间[(2k-1)π,2kπ](k∈Z)上都是增函数,其值从-1增加到1;在每一个闭区间[2kπ,(2k+1)π](k∈Z)上都是减函数,其值从1减小到-1.
5.周期性:
(ⅰ)(观察图象)正弦函数性质如下:
1 正弦函数的图象是有规律不断重复出现的;
2 规律是:每隔2重复出现一次(或者说每隔2k,kZ重复出现);
3 这个规律由诱导公式sin(2k+x)=sinx可以说明.
结论:象这样的函数叫做周期函数.
文字语言:正弦函数值按照一定的规律不断重复地取得。
符号语言:当增加()时,总有.
也即:(1)当自变量增加时,正弦函数的值又重复出现;
(2)对于定义域内的任意,恒成立.
余弦函数也具有同样的性质,这种性质我们就称之为函数的周期性.
(ⅱ) 周期函数定义:对于函数f (x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有:f (x+T)=f (x)那么函数f (x)就叫做周期函数,非零常数T叫做这个函数的周期.
问题:(1)对于函数,有,能否说是它的周期?
(2)正弦函数,是不是周期函数,如果是,周期是多少?
(3)若函数的周期为,则,也是的周期吗?为什么?
(是,其原因为:)
说明: (1)周期函数x定义域M,则必有x+TM, 且若T>0则定义域无上界;T<0则定义域无下界;
(2)“每一个值”只要有一个反例,则f (x)就不为周期函数(如f (x0+t)f (x0));
(3)T往往是多值的(如y=sinx,2,4,…,-2,-4,…都是周期)周期T中最小的正数叫做f (x)的最小正周期(有些周期函数没有最小正周期);
一般结论:函数及函数,的周期.
(三)我也能行
1.画出函数,的简图,并回答下列问题.
① 在上的解集为 .
② 在上的解集为 .
③ 在上的解为 .
2.求使函数取得最大值、最小值的自变量的集合,并分别写出最大值、最小值是什么.
3.(2010湖北—文2)函数 =,的最小正周期为 ( )
A. B. C. D.
4.(2006北京—文2)函数y=1+cosx的图象 ( )
A.关于x轴对称 B.关于y轴对称
C.关于原点对称 D.关于直线x=对称
5.函数的周期是 ,对称轴是 ,对称中心是 ,单调递增区间是 .
三、精点精评
【例1】 函数y=3sin(-2x)在什么区间是减函数?当时,求该函数的单调递减区间.
【例2】 函数y=|sinx|的周期是
【解析】 作出函数y=|sinx|的简图(如下图所示),由图可知函数的周期是.
四、直击高考
1.(2006辽宁—文1) 函数的最小正周期是( )
A ( http: / / wxc. / ) B ( http: / / wxc. / ) C ( http: / / wxc. / ) D ( http: / / wxc. / )
2.函数y=sin(2x+)图象的一条对称轴方程是 ( )
A.x=- B.x=- C.x= D.x=
3.(2007福建—文5)函数的图象 ( )
A ( http: / / wxc. ) 关于点对称 B ( http: / / wxc. ) 关于直线对称
C ( http: / / wxc. ) 关于点对称 D ( http: / / wxc. ) 关于直线对称
4.(2009浙江—理8)已知a是实数,则函数f(x)=1+asinax的图像不可能是 ( )
5.(2004天津—文10) 函数为增函数的区间是 ( )
A. B. C. D.
6.(2009四川—理4)已知函数,下面结论错误的是 ( )
A.函数的最小正周期为 B.函数在区间上是增函数
C.函数的图像关于直线对称 D.函数是奇函数
7.(2007全国II—文3)函数的一个单调增区间是 ( )
A. B. C. D.
8.(2006湖南—文3)设点P是函数的图象C的一个对称中心,若点P到图象C的对称轴上的距离的最小值,则的最小正周期是
A ( http: / / wxc. / ) 2π B ( http: / / wxc. / ) π C ( http: / / wxc. / ) D ( http: / / wxc. / )
9.(2008江苏1)最小正周期为,其中,则 10
心得与体会
-1
1
o
x
y
-
3
2
-1
1
o
x
y
PAGE
6
第 页
与你共勉:要想超越别人,就得先走在他人的前面。 2010-11-23
