垂径定理

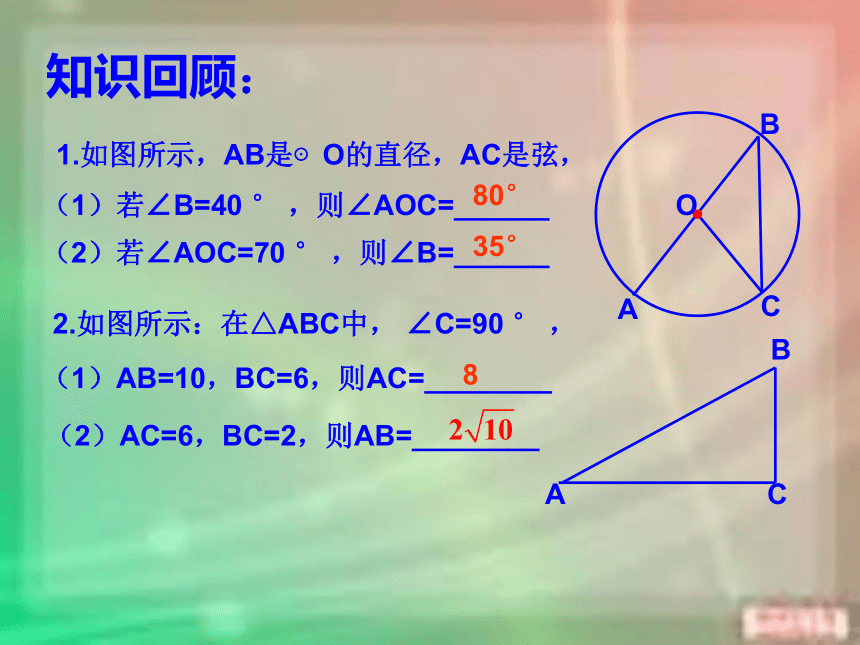
课件45张PPT。垂径定理2010.09东春中学 九（1）班知识回顾：1.如图所示，AB是⊙O的直径，AC是弦，OABC（1）若∠B=40 ° ，则∠AOC=______（2）若∠AOC=70 ° ，则∠B=______2.如图所示：在△ABC中， ∠C=90 ° ，（1）AB=10，BC=6，则AC=________（2）AC=6，BC=2，则AB=________80° 35° 8问题 ：你知道赵州桥吗? 它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦的距离)为7.2m，你能求出赵洲桥主桥拱的半径吗？ 赵州桥主桥拱的半径是多少？ O观察现象：O观察现象：O观察现象：O观察现象：O观察现象：O观察现象：O观察现象：O观察现象：O观察现象：O观察现象：O观察现象：O观察现象：O观察现象：O观察现象：你能得到什么结论？圆是轴对称图形，任何一条直径所在的直线都是它的对称轴。24.1.2 垂直于弦的直径 1.圆的轴对称性：圆是轴对称图形，任何一条直径所在的直线都是它的对称轴。思考：如图，AB是⊙O的一条弦，作直径CD，使CD⊥AB，垂足为E。（1）此图是轴对称图形吗？如果是，它的对称轴是什么？（2）你能发现图中有哪些相等的线段和弧？为什么？ABDCOE24.1.2 垂直于弦的直径 1.圆的轴对称性：圆是轴对称图形，任何一条直径所在的直线都是它的对称轴。思考：如图，AB是⊙O的一条弦，作直径CD，使CD⊥AB，垂足为E。（1）此图是轴对称图形吗？如果是，它的对称轴是什么？（2）你能发现图中有哪些相等的线段和弧？为什么？ABDCOE24.1.2 垂直于弦的直径 1.圆的轴对称性：圆是轴对称图形，任何一条直径所在的直线都是它的对称轴。思考：如图，AB是⊙O的一条弦，作直径CD，使CD⊥AB，垂足为E。（1）此图是轴对称图形吗？如果是，它的对称轴是什么？（2）你能发现图中有哪些相等的线段和弧？为什么？ABDCOE24.1.2 垂直于弦的直径 1.圆的轴对称性：圆是轴对称图形，任何一条直径所在的直线都是它的对称轴。思考：如图，AB是⊙O的一条弦，作直径CD，使CD⊥AB，垂足为E。（1）此图是轴对称图形吗？如果是，它的对称轴是什么？（2）你能发现图中有哪些相等的线段和弧？为什么？ABDCOE24.1.2 垂直于弦的直径 1.圆的轴对称性：圆是轴对称图形，任何一条直径所在的直线都是它的对称轴。思考：如图，AB是⊙O的一条弦，作直径CD，使CD⊥AB，垂足为E。（1）此图是轴对称图形吗？如果是，它的对称轴是什么？（2）你能发现图中有哪些相等的线段和弧？为什么？ABDCOE24.1.2 垂直于弦的直径 1.圆的轴对称性：圆是轴对称图形，任何一条直径所在的直线都是它的对称轴。思考：如图，AB是⊙O的一条弦，作直径CD，使CD⊥AB，垂足为E。（1）此图是轴对称图形吗？如果是，它的对称轴是什么？（2）你能发现图中有哪些相等的线段和弧？为什么？ABDCOE24.1.2 垂直于弦的直径 1.圆的轴对称性：圆是轴对称图形，任何一条直径所在的直线都是它的对称轴。思考：如图，AB是⊙O的一条弦，作直径CD，使CD⊥AB，垂足为E。（1）此图是轴对称图形吗？如果是，它的对称轴是什么？（2）你能发现图中有哪些相等的线段和弧？为什么？ABDCOE24.1.2 垂直于弦的直径 1.圆的轴对称性：圆是轴对称图形，任何一条直径所在的直线都是它的对称轴。思考：如图，AB是⊙O的一条弦，作直径CD，使CD⊥AB，垂足为E。（1）此图是轴对称图形吗？如果是，它的对称轴是什么？（2）你能发现图中有哪些相等的线段和弧？为什么？ABDCOE24.1.2 垂直于弦的直径 1.圆的轴对称性：圆是轴对称图形，任何一条直径所在的直线都是它的对称轴。思考：如图，AB是⊙O的一条弦，作直径CD，使CD⊥AB，垂足为E。（1）此图是轴对称图形吗？如果是，它的对称轴是什么？（2）你能发现图中有哪些相等的线段和弧？为什么？ABDCOE24.1.2 垂直于弦的直径 1.圆的轴对称性：圆是轴对称图形，任何一条直径所在的直线都是它的对称轴。思考：如图，AB是⊙O的一条弦，作直径CD，使CD⊥AB，垂足为E。（1）此图是轴对称图形吗？如果是，它的对称轴是什么？（2）你能发现图中有哪些相等的线段和弧？为什么？ABDCOE24.1.2 垂直于弦的直径 1.圆的轴对称性：圆是轴对称图形，任何一条直径所在的直线都是它的对称轴。思考：如图，AB是⊙O的一条弦，作直径CD，使CD⊥AB，垂足为E。（1）此图是轴对称图形吗？如果是，它的对称轴是什么？（2）你能发现图中有哪些相等的线段和弧？为什么？ABDCOE24.1.2 垂直于弦的直径 1.圆的轴对称性：圆是轴对称图形，任何一条直径所在的直线都是它的对称轴。思考：如图，AB是⊙O的一条弦，作直径CD，使CD⊥AB，垂足为E。（1）此图是轴对称图形吗？如果是，它的对称轴是什么？（2）你能发现图中有哪些相等的线段和弧？为什么？ABDCOE24.1.2 垂直于弦的直径 1.圆的轴对称性：圆是轴对称图形，任何一条直径所在的直线都是它的对称轴。思考：如图，AB是⊙O的一条弦，作直径CD，使CD⊥AB，垂足为E。（1）此图是轴对称图形吗？如果是，它的对称轴是什么？（2）你能发现图中有哪些相等的线段和弧？为什么？ABDCOE24.1.2 垂直于弦的直径 1.圆的轴对称性：圆是轴对称图形，任何一条直径所在的直线都是它的对称轴。思考：如图，AB是⊙O的一条弦，作直径CD，使CD⊥AB，垂足为E。（1）此图是轴对称图形吗？如果是，它的对称轴是什么？（2）你能发现图中有哪些相等的线段和弧？为什么？（A）BDCOEA24.1.2 垂直于弦的直径 1.圆的轴对称性：圆是轴对称图形，任何一条直径所在的直线都是它的对称轴。（A）BDCOEA2.垂径定理：垂直于弦的直径平分弦，并且平分弦所对的两条弧。符号语言： ∵ CD经过圆心O ，CD⊥AB于E，OABDCOEABCODABCODABC应用垂径定理的几个基本图（1）判断下列图形那些符合垂径定理？例1.如图所示，已知AB是⊙O的弦，OC⊥AB于C，且AB=8，OC=3，求⊙O的半径。OACB 连接OA，在Rt△ACO中OA= = =5 所以⊙O的半径为5.练习：1.如图⊙O的半径为8，OC ⊥弦AB于C，且OC=6，求弦长AB。2.如图⊙O的半径为6，弦AB=8，求圆心O到AB的距离。解：∵OC⊥AB于C ∴AC=BC= AB=4已知：已知AB是⊙O的弦，OC⊥AB于C，且AB=8，OC=3，求⊙O的半径。
小结：①作“弦心距”是很重要的一条辅助线，它可以和垂径定理相联系。 ②圆的半径，弦的一半及弦心距可构成直角三角形。因此只要知道圆中半径（直径），弦，弦心距中任意两个量，就可以求出第三个量。 问题 ：你知道赵州桥吗? 它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦的距离)为7.2m，你能求出赵洲桥主桥拱的半径吗？ 赵州桥主桥拱的半径是多少？ DC的中点，CD就是拱高。AB=37.4，CD=7.2 ，∴AD=18.7，设OA=OC=ROD=OC-CD=R-7.2.在Rt△AOD中，OA2 = AD2 + OD2即 R2 = 18.72 + (R-7.2)2 解得 R≈27.9因此，赵州桥的主桥拱的半径约为27.9米。（1）以O为圆心的两个同心圆中，大圆的直径AB交小圆C,D两点，问：AC与BD相等吗？
（2）如图：若将直径向下移动，变为非直径的弦AB，交小圆于C,D两点，是否仍有AC=BD呢？
（3）如图，将大圆去掉，
已知：AC=BD
求证：∠A=∠B
（4）如图，将小圆去掉，若
已知：AC=BD
求证：△OCD是等腰三角形 圆O的半径是5cm,AB、CD是圆O
的两条平行弦，AB=6cm，CD=8cm，
求AB、CD之间的距离。 （1） （2） 发散题：有一截面为圆形的输油管，
内径为650mm,若油面宽为600mm，
求油的深度。·课堂小结 1.圆的轴对称性：（A）BDCOEA2.垂径定理：作业布置：学案相应练习圆是轴对称图形，任何一条直径所在
的直线都是它的对称轴。垂直于弦的直径平分弦，并且平分弦
所对的两条弧。
体会.分享说出你这节课的收获和体验，让大家与你一起分享！！！