24.1.2垂直于弦的直径(2)
文档属性
| 名称 | 24.1.2垂直于弦的直径(2) |

|
|
| 格式 | rar | ||
| 文件大小 | 212.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-11-24 09:27:00 | ||
图片预览


文档简介
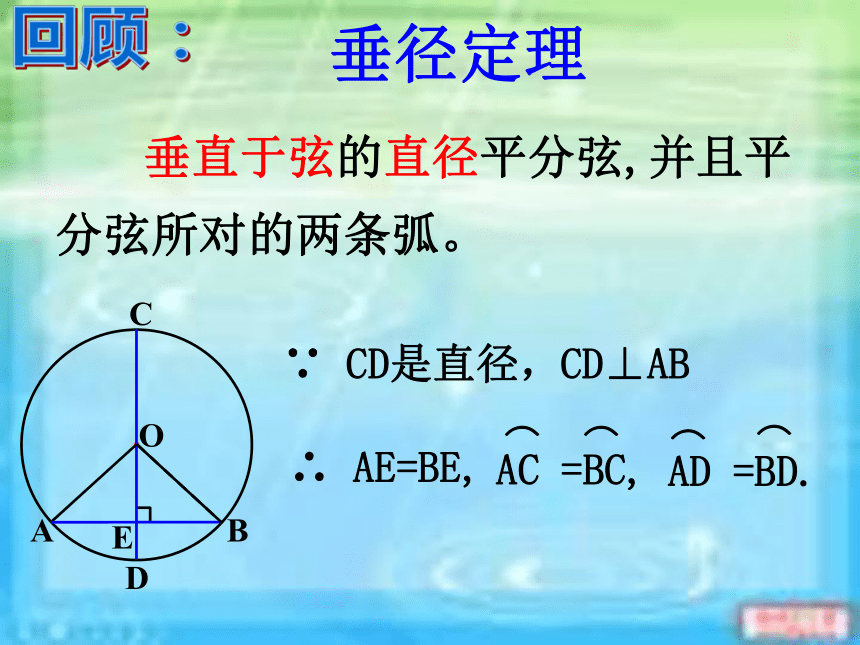
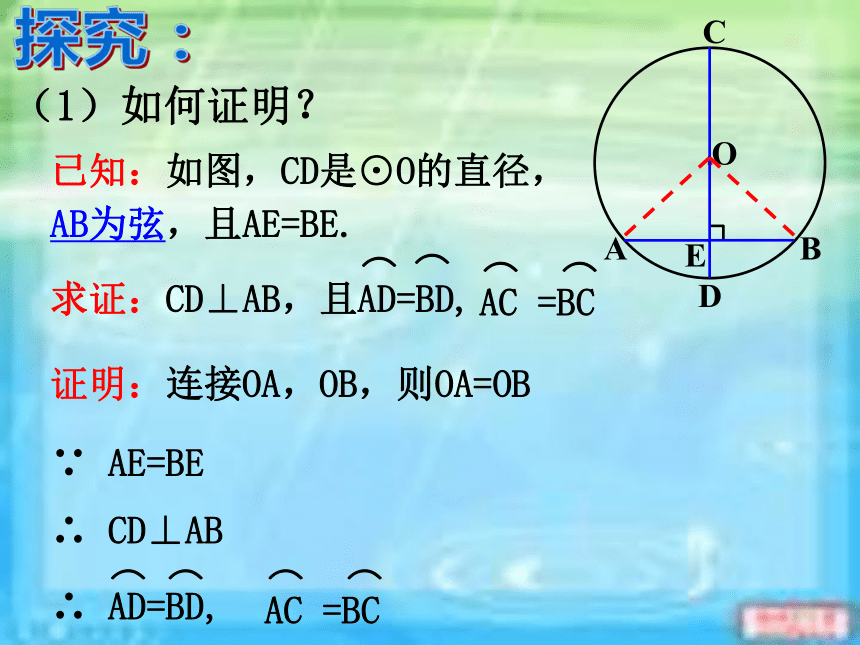
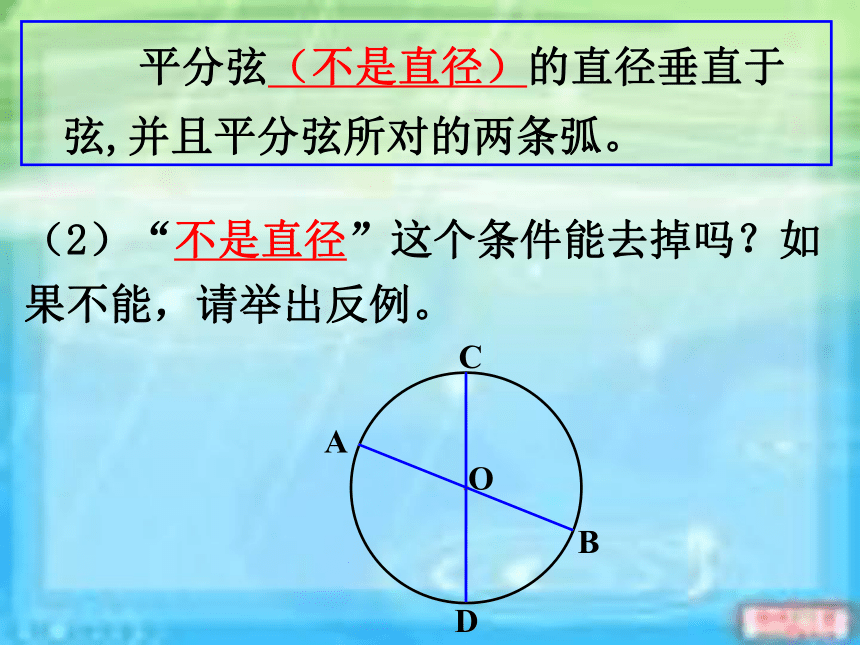
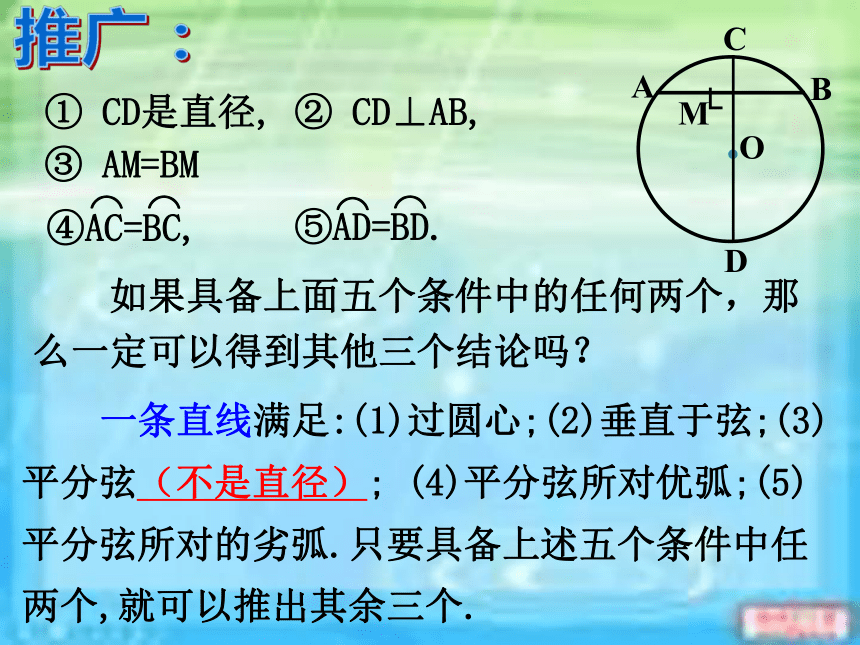
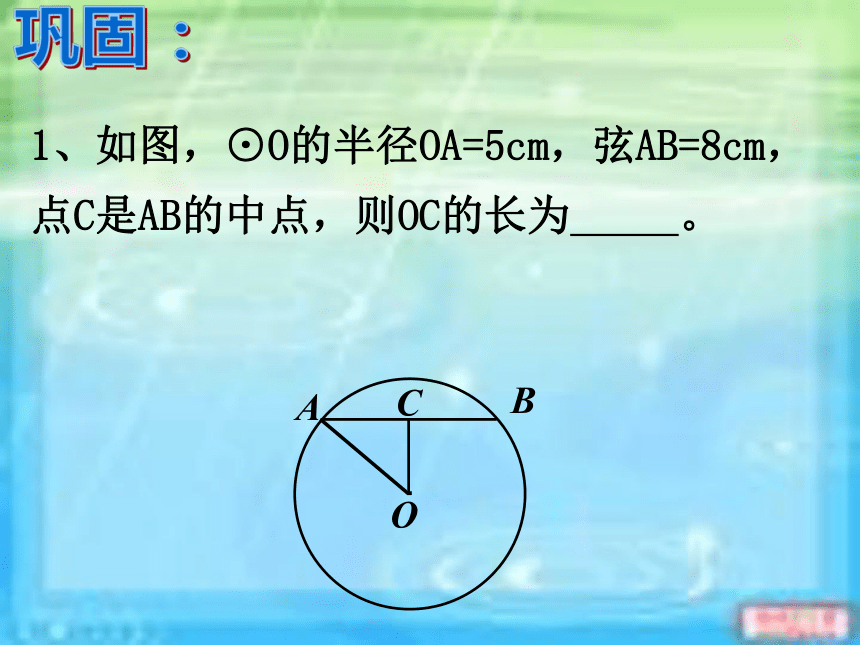
课件14张PPT。24.1.2 垂直于弦的直径(2) 人教版九年级上册东春中学九(1)班垂径定理 垂直于弦的直径平分弦,并且平分弦所对的两条弧。CD⊥AB ∵ CD是直径,∴ AE=BE,·OABCDE回顾:垂径定理推论 平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。∴ CD⊥AB, ∵ CD是直径, AE=BE·OABCDE新知:(1)如何证明?探究:已知:如图,CD是⊙O的直径,AB为弦,且AE=BE.证明:连接OA,OB,则OA=OB∵ AE=BE∴ CD⊥AB(2)“不是直径”这个条件能去掉吗?如果不能,请举出反例。 平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。① CD是直径, ② CD⊥AB, ③ AM=BM 如果具备上面五个条件中的任何两个,那么一定可以得到其他三个结论吗? 一条直线满足:(1)过圆心;(2)垂直于弦;(3)平分弦(不是直径); (4)平分弦所对优弧;(5)平分弦所对的劣弧.只要具备上述五个条件中任两个,就可以推出其余三个.推广:1、如图,⊙O的半径OA=5cm,弦AB=8cm,点C是AB的中点,则OC的长为 。·OABC巩固:巩固训练判断下列说法的正误 ①平分弧的直径必平分弧所对的弦 ②平分弦的直线必垂直弦 ③垂直于弦的直径平分这条弦 ④平分弦的直径垂直于这条弦 ⑤弦的垂直平分线是圆的直径 ⑥平分弦所对的一条弧的直径必垂直这条弦 ⑦在圆中,如果一条直线经过圆心且平分弦,
必平分此弦所对的弧 ⑧分别过弦的三等分点作弦的垂线,将弦所对
的两条弧分别三等分 2.已知,⊙O的直径AB和弦CD相交于点E,AE=6厘米,EB=2厘米,∠BED=30°,
求CD的长。说明:
解决有关圆的问题,
常常需要添加辅助线,
针对各种具体情况,辅助线的添加有一定的规律,本例和上例中作“垂直于弦的直径”就是一个很好的例证。练习F1.在直径是20cm的⊙O中,∠AOB的度数是60°, 那么弦AB的弦心距是 . 圆的圆心到圆上弦的距离叫做弦心距。2.弓形的弦长为6cm,弓形的高为2cm,则这弓形所在的圆的半径为 . 综合运用练习
如图,⊙O中CD是弦,AB是直径,AE⊥CD于E,BF⊥CD于F,求证:CE=DF。小结知二具五由(2)(3)推(1)(4)(5)时所平分的弦是非直径的弦 (1)垂直于弦(2)过圆心(3)平分弦(4)平分优弧(5)平分劣弧推论2 两条平行弦所夹的弧相等 辅助线的一般作法:
有弦作弦心距或连半径结束寄语不学自知,不问自晓,古今行事,未之有也.再见
必平分此弦所对的弧 ⑧分别过弦的三等分点作弦的垂线,将弦所对
的两条弧分别三等分 2.已知,⊙O的直径AB和弦CD相交于点E,AE=6厘米,EB=2厘米,∠BED=30°,
求CD的长。说明:
解决有关圆的问题,
常常需要添加辅助线,
针对各种具体情况,辅助线的添加有一定的规律,本例和上例中作“垂直于弦的直径”就是一个很好的例证。练习F1.在直径是20cm的⊙O中,∠AOB的度数是60°, 那么弦AB的弦心距是 . 圆的圆心到圆上弦的距离叫做弦心距。2.弓形的弦长为6cm,弓形的高为2cm,则这弓形所在的圆的半径为 . 综合运用练习
如图,⊙O中CD是弦,AB是直径,AE⊥CD于E,BF⊥CD于F,求证:CE=DF。小结知二具五由(2)(3)推(1)(4)(5)时所平分的弦是非直径的弦 (1)垂直于弦(2)过圆心(3)平分弦(4)平分优弧(5)平分劣弧推论2 两条平行弦所夹的弧相等 辅助线的一般作法:
有弦作弦心距或连半径结束寄语不学自知,不问自晓,古今行事,未之有也.再见
同课章节目录
