(人教新课标八年级上)数学:12.3等腰三角形(第2课时)课件1
文档属性
| 名称 | (人教新课标八年级上)数学:12.3等腰三角形(第2课时)课件1 |  | |
| 格式 | rar | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-11-23 17:50:00 | ||
图片预览





文档简介
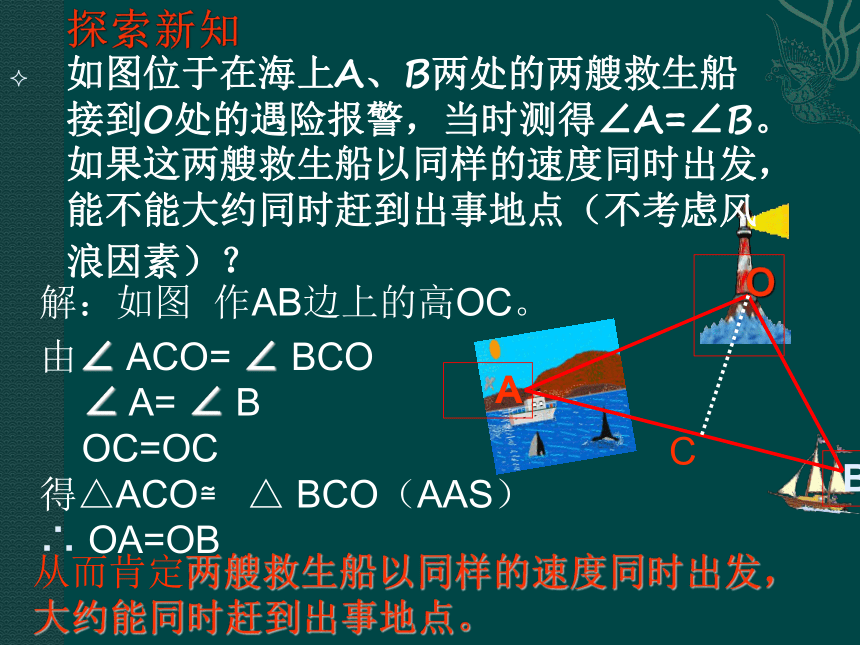
课件22张PPT。等腰三角形的判定12.3.1探索新知如图位于在海上A、B两处的两艘救生船接到O处的遇险报警,当时测得∠A=∠B。如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)? 解:如图 作AB边上的高OC。由∠ ACO= ∠ BCO
∠ A= ∠ B
OC=OC
得△ACO≌ △ BCO(AAS)
∴ OA=OB从而肯定两艘救生船以同样的速度同时出发,
大约能同时赶到出事地点。一、复习:1、等腰三角形的性质定理是什么?等腰三角形的两个底角相等。
(可以简称:等边对等角)2、这个定理的逆命题是什么?如果一个三角形有两个角相等,
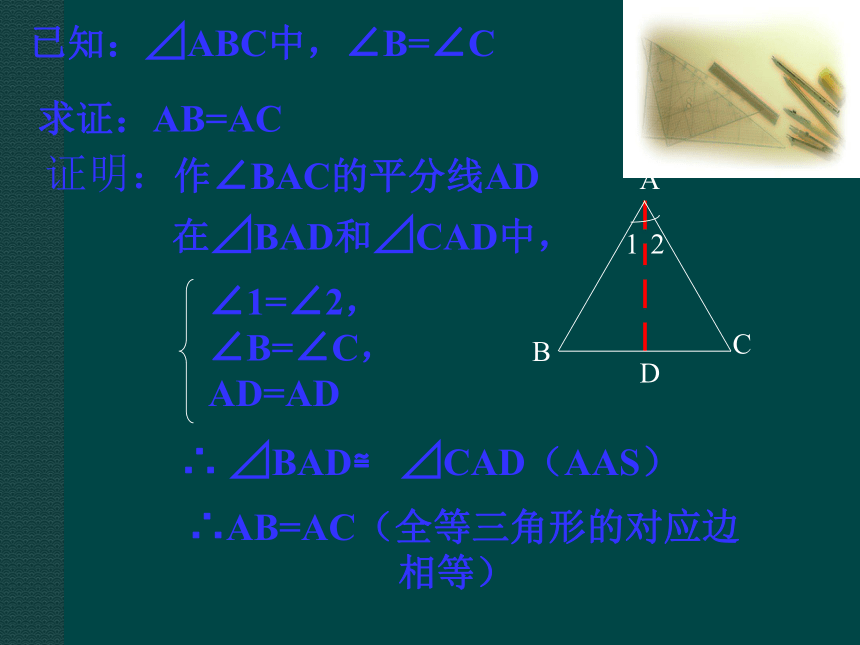
那么这个三角形是等腰三角形。3、这个命题正确吗?你能证明吗?已知:⊿ABC中,∠B=∠C求证:AB=AC证明:作∠BAC的平分线AD在⊿BAD和⊿CAD中,∠1=∠2,
∠B=∠C,
AD=AD∴ ⊿BAD≌ ⊿CAD(AAS)∴AB=AC(全等三角形的对应边
相等)12等腰三角形的判定定理 如果一个三角形有两个角相等,那么这个三角形是等腰三角形。
简写成:等角对等边探究:等腰三角形的性质定理和判定定理 互为逆命题等腰三角形的判定定理 与性质定理有何不同? 性质是:等边 等角判定是:等角 等边求证:AB=AC证明:∵ AE ∥ BC
∴∠DAE= ∠ B( )
∠ EAC= ∠ C ( )
又∠DAE= ∠EAC
∴ ∠B= ∠C
∴AB=AC( )
已知:AE是△ ABC的外角平分线,
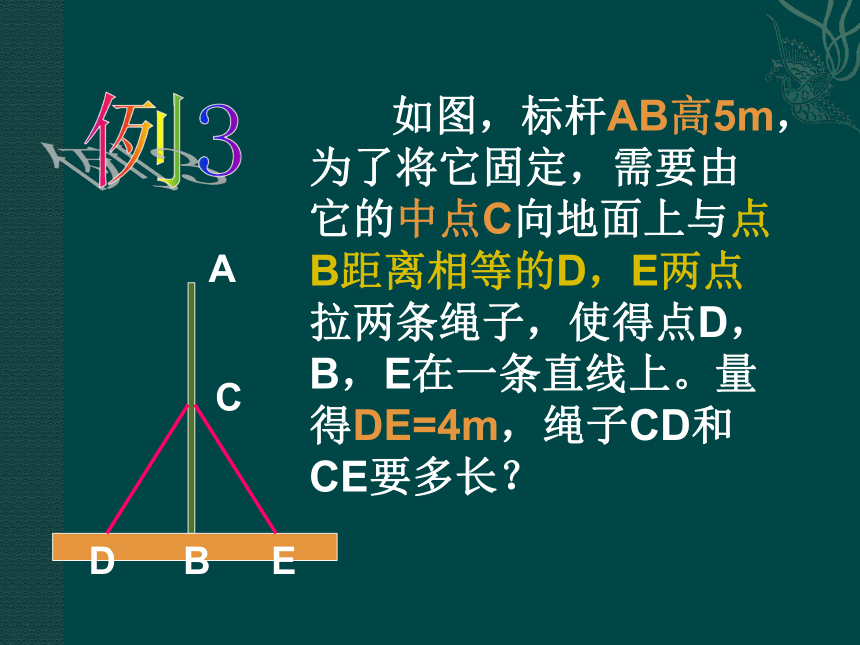
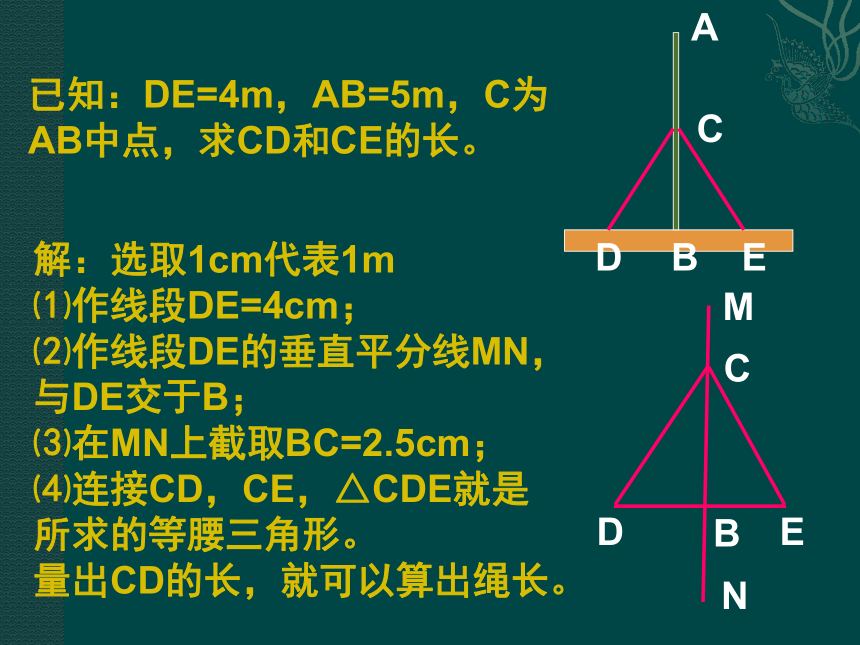
且AE ∥ BC.两直线平行,同位角相等两直线平行,内错角相等等角对等边例3 如图,标杆AB高5m,为了将它固定,需要由它的中点C向地面上与点B距离相等的D,E两点拉两条绳子,使得点D,B,E在一条直线上。量得DE=4m,绳子CD和CE要多长?解:选取1cm代表1m
⑴作线段DE=4cm;
⑵作线段DE的垂直平分线MN,
与DE交于B;
⑶在MN上截取BC=2.5cm;
⑷连接CD,CE,△CDE就是
所求的等腰三角形。
量出CD的长,就可以算出绳长。已知:DE=4m,AB=5m,C为
AB中点,求CD和CE的长。练习3∠1=720 ∠2=360等腰三角形有: ⊿ABC 、⊿ABD、⊿BCD综合运用1、如图△ABC中,AB=AC,∠B=36°,D、E分别是BC边上两点,且∠ADE=∠AED=2∠BAD,则图中等腰三角形有( )个。
C共有6个。
即△ABC、△ ADE、△ AEC、△ ABD、△ ABE。△ ADC、练习4等腰直角三角形有: ⊿ABC ⊿ACD ⊿BCD证明:∵ AD ∥BC
∴∠ADB=∠DBC
∵∠ABD=∠DBC
∴∠ABD=∠ADB
∴AB=AD(等角对等边)已知:如图,AD ∥BC,BD平分∠ABC。
求证:AB=AD2.如图,五角星中有______个等腰三角形。10找一找练一练1.已知等腰三角形的两边长分别是4和6,则它的周长是( )
A、14 B、15 C、16 D、14或16
D 若把此等腰三角形的两边长改为3和7,则它的周长应是多少?
2、如图,把一张矩形的纸沿对角线折叠,重合
的部分是一个等腰三角形吗?为什么?123解:重合部分是等腰三角形。理由:由ABDC是矩形知
AC∥BD
∴∠ 3= ∠ 2由沿对角线折叠知
∠ 1 = ∠ 2∴ ∠ 1= ∠ 3
∴ BG=GC(等角对等边)拓广探索如图 是十堰市郧县汉江斜拉桥的剖面图,BC是桥面,AD是桥墩,设计大桥时工程师要求斜拉的钢绳AB等于AC,大桥建成后,工程技术人员要对大桥进行验收,由于桥墩很高,无法直接测量钢绳AB、AC的长度,请你用三种方法检验AB、AC的长度是否相等?(检验工具
为刻度尺,量角器。检验时人只能站在桥上)思考:
1 有几种方法能说明AB、AC相等?
2 根据提供的工具和条件,你能得到哪些准确数据?说明你的操作过程和理由。检验方法一:用量角器度量∠ B、 ∠ C的大小,
若∠B=∠ C,则可得AB=AC。方法二:如图用刻度尺测量BD、DC的长度,
若BD=DC,又AD⊥BC,则AB=AC。若上述三种方法都不满足,则AB不等于AC。方法三:用刻度尺在∠ B、 ∠ C的两边上分别
度量BE、CF、BP、CQ的长度(使EP、EQ可
以度量)
使BE=CF,BP=CQ,再度量EP、FQ的长度,
若EP=FQ,则AB=AC。例2:上午10 时,一条船从A处出发以20海里每小时的速度向正北航行,中午12时到达B处,从A、B望灯塔C,测得∠NAC=40°, ∠NBC=80°求从B处到灯塔C的距离NBAC80°40°北解:∵∠NBC=∠A+∠C
∴∠C=80°- 40°= 40°
∴ BA=BC(等角对等边)
∵AB=20(12-10)=40
∴BC=40
答:B处到达灯塔C40海里练习32、已知:如图(9),AD∥BC,BD平分∠ABC,
求证:AB=AD。ABCD312(9)证明:∵BD平分∠ABC
∴∠1=∠2
∵AD∥BC
∴∠2=∠3
∴∠1=∠3
∴AB=AD(等角对等边)4、已知:如图(11),AB=AD,∠ADC=∠ABC,
求证:CB=CD。证明:连接BD
∵AB=AD
∴∠ABD∠ADB(等边对等角)
又∵∠ABC=∠ADC
∴∠ABC-∠ABD=∠ADC-∠ADB
即,∠CBD=∠CDB
∴CB=CD(等角对等边)(11)3、已知:如图(10),∠1=∠2, ∠3=∠4,DE∥BC;
求证:DE=DB+EC。ABDCEF1234(10)证明:
∵DE∥BC
∴∠2=∠DFB,∠3=∠EFC
又∵∠1=∠2,∠3=∠4
∴∠1=∠DFB,∠4=∠EFC
∴DF=BD, EF = EC
又∵DE=DF+EF
∴DE=DB+EC
∠ A= ∠ B
OC=OC
得△ACO≌ △ BCO(AAS)
∴ OA=OB从而肯定两艘救生船以同样的速度同时出发,
大约能同时赶到出事地点。一、复习:1、等腰三角形的性质定理是什么?等腰三角形的两个底角相等。
(可以简称:等边对等角)2、这个定理的逆命题是什么?如果一个三角形有两个角相等,
那么这个三角形是等腰三角形。3、这个命题正确吗?你能证明吗?已知:⊿ABC中,∠B=∠C求证:AB=AC证明:作∠BAC的平分线AD在⊿BAD和⊿CAD中,∠1=∠2,
∠B=∠C,
AD=AD∴ ⊿BAD≌ ⊿CAD(AAS)∴AB=AC(全等三角形的对应边
相等)12等腰三角形的判定定理 如果一个三角形有两个角相等,那么这个三角形是等腰三角形。
简写成:等角对等边探究:等腰三角形的性质定理和判定定理 互为逆命题等腰三角形的判定定理 与性质定理有何不同? 性质是:等边 等角判定是:等角 等边求证:AB=AC证明:∵ AE ∥ BC
∴∠DAE= ∠ B( )
∠ EAC= ∠ C ( )
又∠DAE= ∠EAC
∴ ∠B= ∠C
∴AB=AC( )
已知:AE是△ ABC的外角平分线,
且AE ∥ BC.两直线平行,同位角相等两直线平行,内错角相等等角对等边例3 如图,标杆AB高5m,为了将它固定,需要由它的中点C向地面上与点B距离相等的D,E两点拉两条绳子,使得点D,B,E在一条直线上。量得DE=4m,绳子CD和CE要多长?解:选取1cm代表1m
⑴作线段DE=4cm;
⑵作线段DE的垂直平分线MN,
与DE交于B;
⑶在MN上截取BC=2.5cm;
⑷连接CD,CE,△CDE就是
所求的等腰三角形。
量出CD的长,就可以算出绳长。已知:DE=4m,AB=5m,C为
AB中点,求CD和CE的长。练习3∠1=720 ∠2=360等腰三角形有: ⊿ABC 、⊿ABD、⊿BCD综合运用1、如图△ABC中,AB=AC,∠B=36°,D、E分别是BC边上两点,且∠ADE=∠AED=2∠BAD,则图中等腰三角形有( )个。
C共有6个。
即△ABC、△ ADE、△ AEC、△ ABD、△ ABE。△ ADC、练习4等腰直角三角形有: ⊿ABC ⊿ACD ⊿BCD证明:∵ AD ∥BC
∴∠ADB=∠DBC
∵∠ABD=∠DBC
∴∠ABD=∠ADB
∴AB=AD(等角对等边)已知:如图,AD ∥BC,BD平分∠ABC。
求证:AB=AD2.如图,五角星中有______个等腰三角形。10找一找练一练1.已知等腰三角形的两边长分别是4和6,则它的周长是( )
A、14 B、15 C、16 D、14或16
D 若把此等腰三角形的两边长改为3和7,则它的周长应是多少?
2、如图,把一张矩形的纸沿对角线折叠,重合
的部分是一个等腰三角形吗?为什么?123解:重合部分是等腰三角形。理由:由ABDC是矩形知
AC∥BD
∴∠ 3= ∠ 2由沿对角线折叠知
∠ 1 = ∠ 2∴ ∠ 1= ∠ 3
∴ BG=GC(等角对等边)拓广探索如图 是十堰市郧县汉江斜拉桥的剖面图,BC是桥面,AD是桥墩,设计大桥时工程师要求斜拉的钢绳AB等于AC,大桥建成后,工程技术人员要对大桥进行验收,由于桥墩很高,无法直接测量钢绳AB、AC的长度,请你用三种方法检验AB、AC的长度是否相等?(检验工具
为刻度尺,量角器。检验时人只能站在桥上)思考:
1 有几种方法能说明AB、AC相等?
2 根据提供的工具和条件,你能得到哪些准确数据?说明你的操作过程和理由。检验方法一:用量角器度量∠ B、 ∠ C的大小,
若∠B=∠ C,则可得AB=AC。方法二:如图用刻度尺测量BD、DC的长度,
若BD=DC,又AD⊥BC,则AB=AC。若上述三种方法都不满足,则AB不等于AC。方法三:用刻度尺在∠ B、 ∠ C的两边上分别
度量BE、CF、BP、CQ的长度(使EP、EQ可
以度量)
使BE=CF,BP=CQ,再度量EP、FQ的长度,
若EP=FQ,则AB=AC。例2:上午10 时,一条船从A处出发以20海里每小时的速度向正北航行,中午12时到达B处,从A、B望灯塔C,测得∠NAC=40°, ∠NBC=80°求从B处到灯塔C的距离NBAC80°40°北解:∵∠NBC=∠A+∠C
∴∠C=80°- 40°= 40°
∴ BA=BC(等角对等边)
∵AB=20(12-10)=40
∴BC=40
答:B处到达灯塔C40海里练习32、已知:如图(9),AD∥BC,BD平分∠ABC,
求证:AB=AD。ABCD312(9)证明:∵BD平分∠ABC
∴∠1=∠2
∵AD∥BC
∴∠2=∠3
∴∠1=∠3
∴AB=AD(等角对等边)4、已知:如图(11),AB=AD,∠ADC=∠ABC,
求证:CB=CD。证明:连接BD
∵AB=AD
∴∠ABD∠ADB(等边对等角)
又∵∠ABC=∠ADC
∴∠ABC-∠ABD=∠ADC-∠ADB
即,∠CBD=∠CDB
∴CB=CD(等角对等边)(11)3、已知:如图(10),∠1=∠2, ∠3=∠4,DE∥BC;
求证:DE=DB+EC。ABDCEF1234(10)证明:
∵DE∥BC
∴∠2=∠DFB,∠3=∠EFC
又∵∠1=∠2,∠3=∠4
∴∠1=∠DFB,∠4=∠EFC
∴DF=BD, EF = EC
又∵DE=DF+EF
∴DE=DB+EC
