圆周角

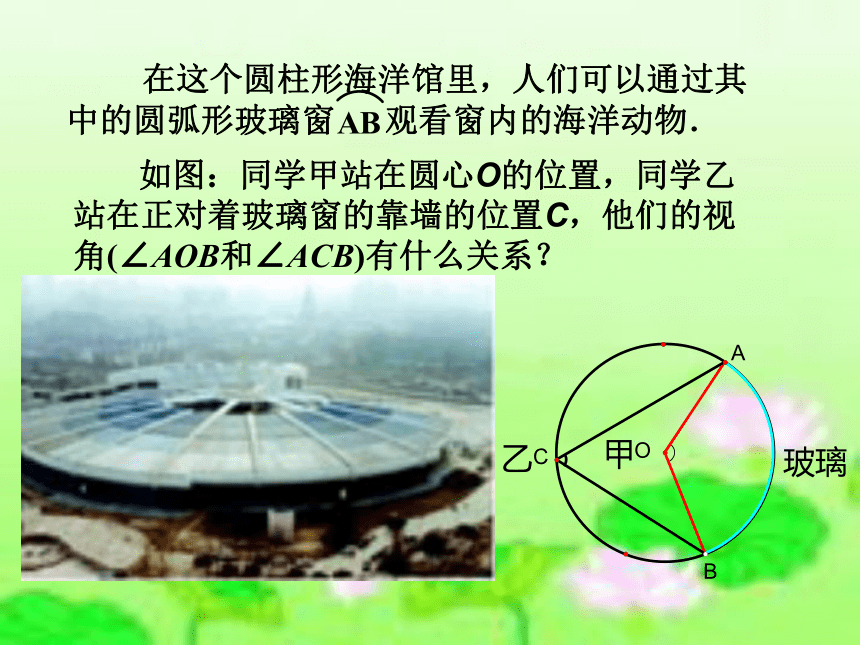
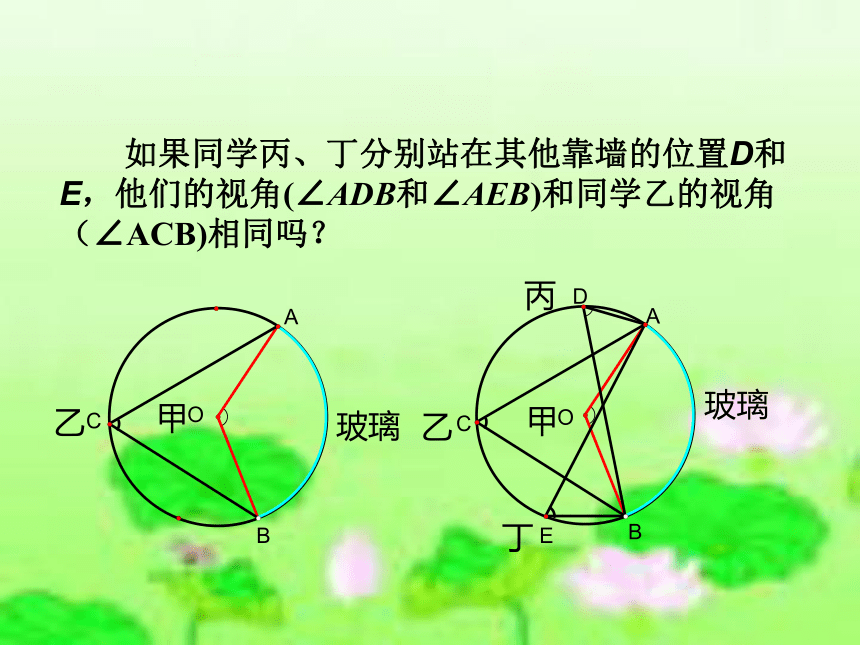
课件28张PPT。圆周角（一）东春中学九（1）班2010年9月 在这个圆柱形海洋馆里，人们可以通过其 中的圆弧形玻璃窗 观看窗内的海洋动物． 如图：同学甲站在圆心O的位置，同学乙站在正对着玻璃窗的靠墙的位置C，他们的视角(∠AOB和∠ACB)有什么关系？ 如果同学丙、丁分别站在其他靠墙的位置D和E，他们的视角(∠ADB和∠AEB)和同学乙的视角（∠ACB)相同吗？
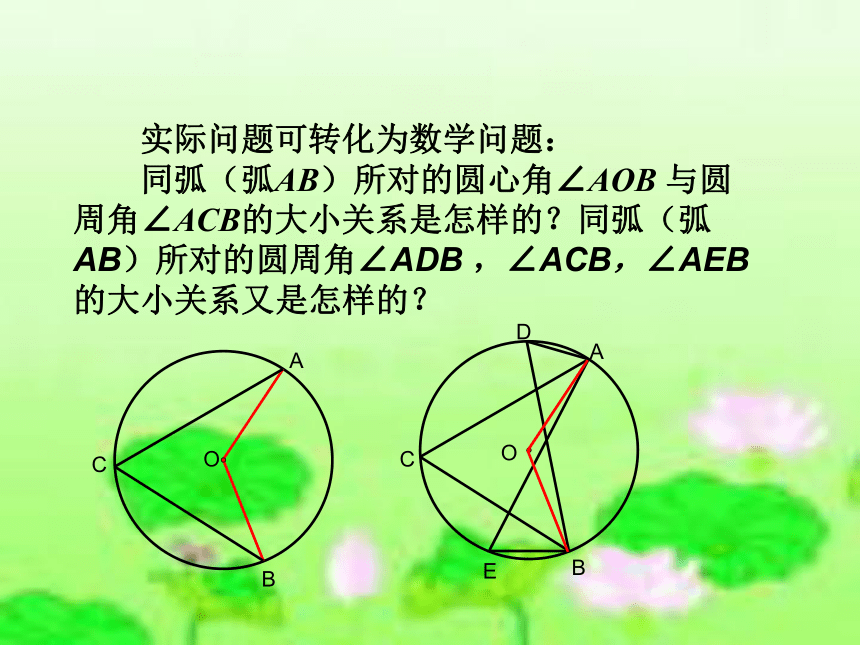
实际问题可转化为数学问题：
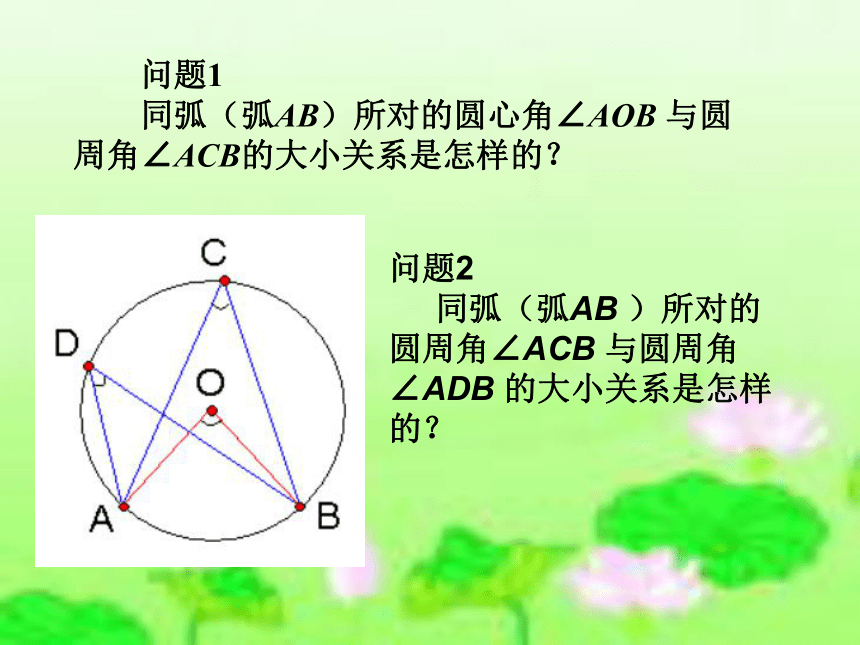
同弧（弧AB）所对的圆心角∠AOB 与圆周角∠ACB的大小关系是怎样的？同弧（弧AB）所对的圆周角∠ADB ，∠ACB，∠AEB的大小关系又是怎样的？
A 复习旧知：请说说我们是如何给圆心角下定义的，试回答？顶点在圆心的角叫圆心角。考考你：你能仿照圆心角的定义，
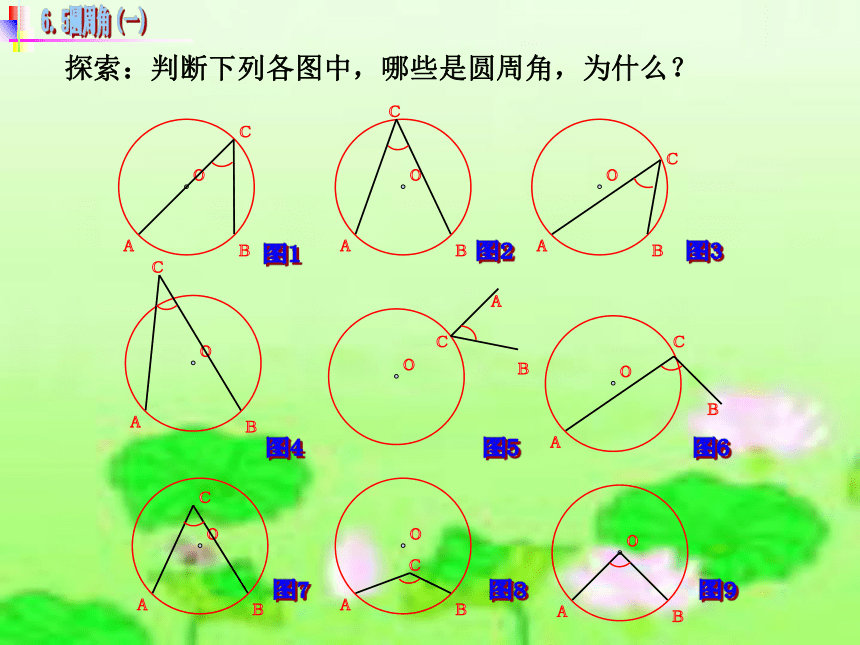
给下图中象∠ACB 这样的角下个定义吗？顶点在圆上，并且两边都和圆相交的角叫做圆周角． 探索：判断下列各图中，哪些是圆周角，为什么？ oABoABoABoABoABoABoABoABCCCCCCCC图1图2图3图4图5图6图7图8图9 问题1
同弧（弧AB）所对的圆心角∠AOB 与圆周角∠ACB的大小关系是怎样的？ 问题2
同弧（弧AB ）所对的圆周角∠ACB 与圆周角∠ADB 的大小关系是怎样的？
画一个圆心角,然后再画同弧所对的圆周角.1.同一条弧你能画多少个圆周角?多少个圆
心角?用量角器量一量这些
圆周角你有何发现？2.再用量角器量出圆心角的度数,你有何发现 呢?发现:一条弧所对的圆周角等于它所对的圆心角的一半.探索2:发现:在同圆(或等圆)中,同弧或等弧所
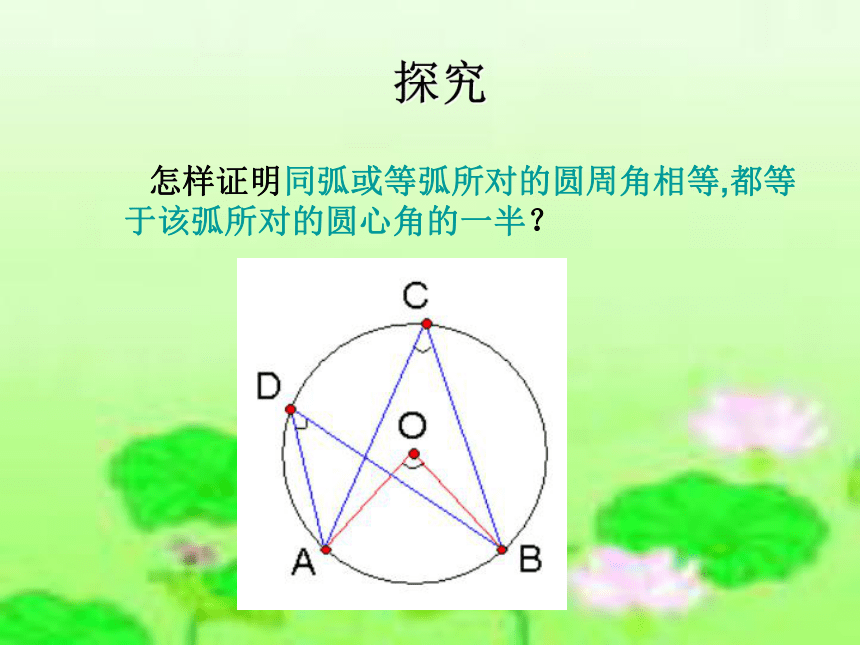
对的圆周角相等探究怎样证明同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半？ 做一做 问题1
在圆上任取一个圆周角，观察圆心与圆周角的位置关系有几种情况？ 问题2
当圆心在圆周角的一边上时，如何证明？ 活动3 做一做分三种情况来证明：
（1）圆心在∠BAC的一边上.
问题3
另外两种情况如何证明呢？ 活动3 做一做（2）圆心在∠BAC的内部.（3）圆心在∠BAC的外部.D 得证: 在同圆或等圆中，同弧所对的圆周角都等于这条弧所对的圆心角的一半，进而得出同弧所对的圆周角相等。
辨析:（1）在同圆或等圆中，同弧或等弧所对的圆周角相等。（ ）
√ （2）在同圆或等圆中，同弦或等弦所对的圆周角一定相等。（ ）×圆周角定理定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半。
同学丙、丁的视角(∠ADB和∠AEB)和同学乙的视角（∠ACB)相同,且都等于同学甲的视角(∠AOB)的一半
练习:已知:点A、B、C、D在同一个圆上,找出图中相等的圆周角角？ABCD∠1 = ∠4∠5 = ∠8∠2 = ∠7∠3 = ∠6方法点拔：由同弧来找相等的圆周角例题　1、在⊙O中，∠CBD=30° ,∠BDC=20°,求∠A　1、在⊙O中，∠CBD=30° ,∠BDC=20°,求∠A　　 2、如图，在⊙O中，AB为直径，CB = CF,
弦CG⊥AB，交AB于D，交BF于E
求证：BE=EC
例题⌒⌒问题2
半圆（或直径）所对的圆周角是多少度？ 问题3
90°的圆周角所对的弦是什么? 圆周角定理的推论
推论：半圆（或直径）所对的圆周角是直角， 90°的圆周角所对的弦是直径。 答：在同圆或等圆中，如果两个圆周角相等，则它们同弧所对的圆心角相等，由圆心角与弧、弦的关系定理可知相等圆心角所对的弧也相等。
所以在同圆或等圆中，如果两个圆周角相等，它们所对的弧一定相等。 问题4
　　在同圆或等圆中，如果两个圆周角相等，
它们所对的弧一定相等吗？为什么？ 问题６ 如图, ⊙O的直径 AB 为10 cm，弦 AC 为６cm, ∠ACB 的平分线交⊙O于 D, 求BC、AD、BD的长. 结论：在同圆或等圆中，若圆周角相等，则它们所对的弧也相等。相应的它们所对的弦也相等。1.圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角.2.在同圆(或等圆)中，同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半；相等的圆周角所对的弧相等。3.半圆或直径所对的圆周角都相等，都等于90°
90°的圆周角所对的弦是圆的直径小结:作业:1、书本94页第4、11题
2、名师学案相关练习