勾股定理
图片预览



文档简介
课件23张PPT。 18.1勾股定理东春中学
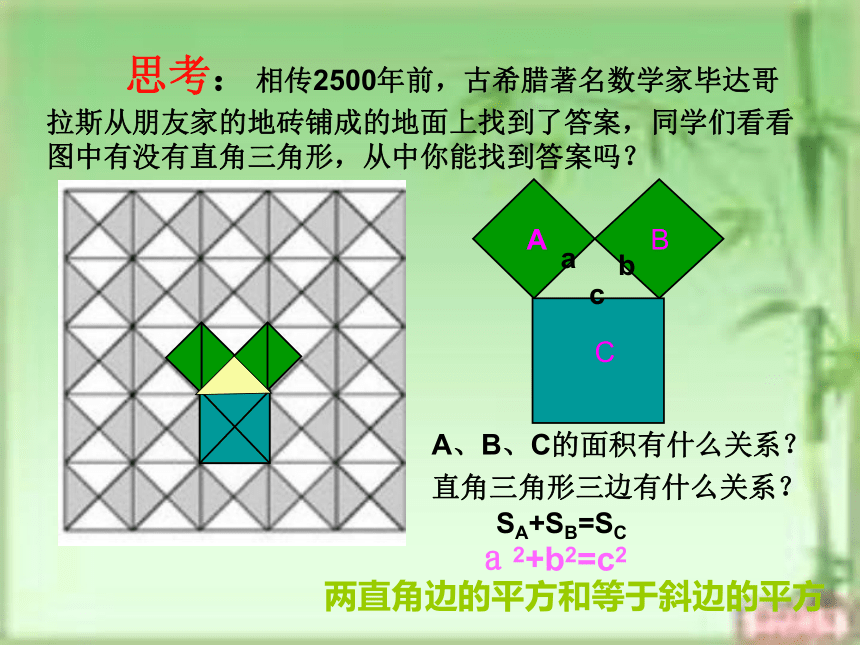
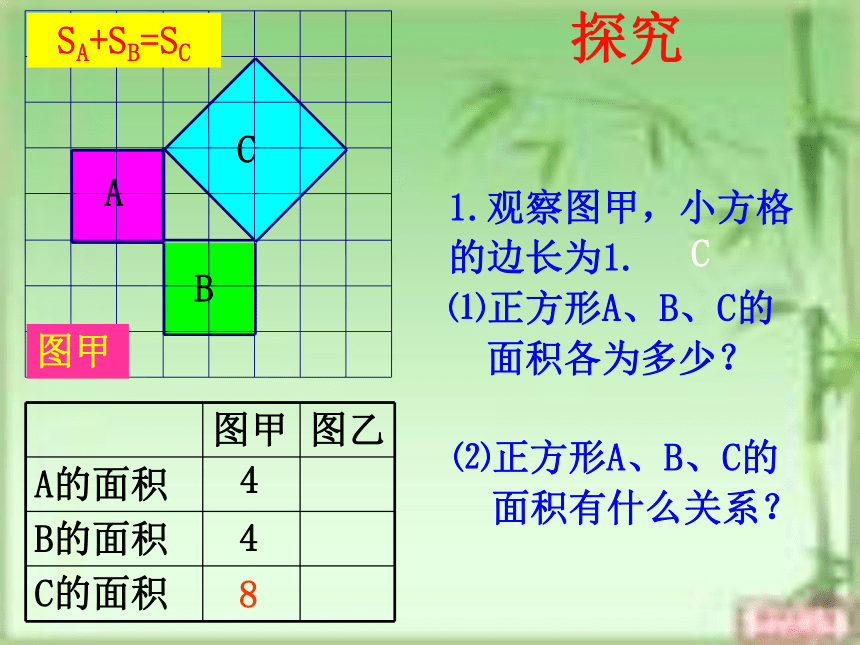
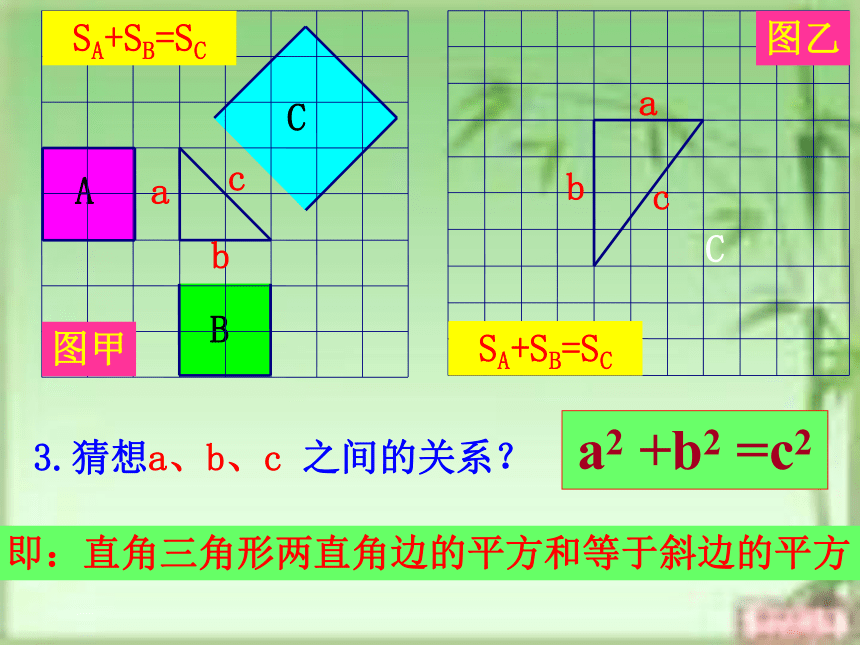
八(2)班这就是本届大会会徽的图案.你见过这个图案吗?你听说过勾股定理吗? 这个图案是我国汉代数学家赵爽在证明勾股定理时用到的,被称为“赵爽弦图”. 思考: 相传2500年前,古希腊著名数学家毕达哥拉斯从朋友家的地砖铺成的地面上找到了答案,同学们看看图中有没有直角三角形,从中你能找到答案吗?A、B、C的面积有什么关系?直角三角形三边有什么关系?SA+SB=SC两直角边的平方和等于斜边的平方a2+b2=c2abc448SA+SB=SCC图甲1.观察图甲,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?⑵正方形A、B、C的
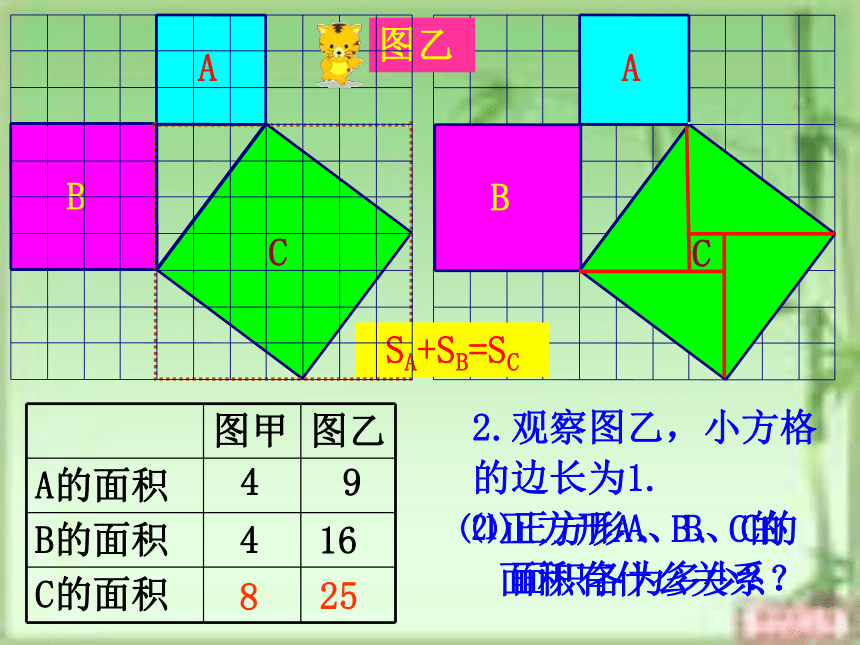
面积有什么关系?探究C图乙2.观察图乙,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?91625⑵正方形A、B、C的
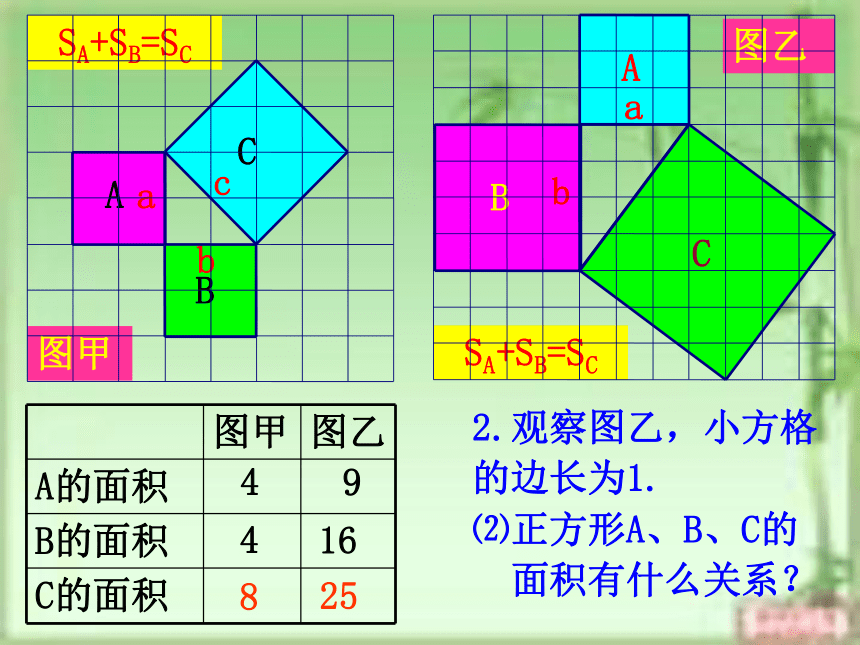
面积有什么关系?448SA+SB=SC图乙2.观察图乙,小方格
的边长为1.91625SA+SB=SC⑵正方形A、B、C的
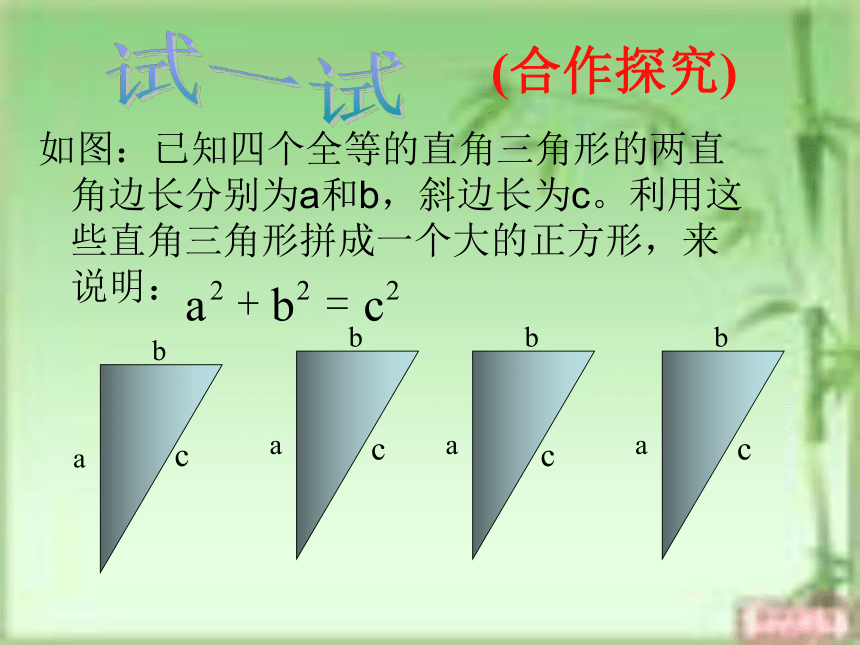
面积有什么关系?448SA+SB=SC图甲abcabc3.猜想a、b、c 之间的关系?a2 +b2 =c2即:直角三角形两直角边的平方和等于斜边的平方命题1:如果直角三角形的两直角边长分别为a、b,斜边长为c,那么a2+b2=c2。abc你能证明这个命题是正确的命题吗?如图:已知四个全等的直角三角形的两直角边长分别为a和b,斜边长为c。利用这些直角三角形拼成一个大的正方形,来说明:
试一试(合作探究) ccc(a-b)2小正方形的面积怎样表示?(a+b)2=a2 + b2 + 2ab = c2+2ab可得: a2 + b2 = c2方法(二):对比两种方法,
你能得到什么?方法(一): 定理:经过证明被确认为正确的命题叫做定理。 这种证法是美国第二十任总统伽菲尔德发现的,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就称这一证法称为“总统”证法。
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”. 勾股定理如果直角三角形两直角边分别为a、b,斜边为c,那么即 直角三角形两直角边的平方和等于斜边的平方。勾股弦a2 + b2 = c2结论变形c2 = a2 + b2练习:
1、求下列图中字母所表示的正方形的面积=625=1442、求出下列直角三角形中未知边的长度解:由勾股定理得:x2 =36+64x2 =100x2=62+82∴ x=10∵ x2+52=132∴ x2=132-52x2 =169-25x2 =144∴ x=12∵ x > 0∵ x > 01.如图,这了测得湖两岸点A和点C间的距离,一个观测者在点B设立了一根标杆,使∠ACB=90°.测得AB=200m,BC=160m,根据测量结果求点A,C间的距离.ACB120m200m160m2、如图,受台风麦莎影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?小结:说说这节课你有什么收获?勾股小常识:勾股数
1、 a2+b2 =c2,满足(a,b,c)=1,a,b,c为基本勾股数.如:3、4、5 ; 5、12、 13;6、8、10;7、24、25……
2、如果a,b,c是一组勾股数,则ka、kb、kc(k为正整数)也是一组勾股数,如:6、8、10;9、12、15……
3、一组勾股数中必有一个数是5倍数。
再见!
八(2)班这就是本届大会会徽的图案.你见过这个图案吗?你听说过勾股定理吗? 这个图案是我国汉代数学家赵爽在证明勾股定理时用到的,被称为“赵爽弦图”. 思考: 相传2500年前,古希腊著名数学家毕达哥拉斯从朋友家的地砖铺成的地面上找到了答案,同学们看看图中有没有直角三角形,从中你能找到答案吗?A、B、C的面积有什么关系?直角三角形三边有什么关系?SA+SB=SC两直角边的平方和等于斜边的平方a2+b2=c2abc448SA+SB=SCC图甲1.观察图甲,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?⑵正方形A、B、C的
面积有什么关系?探究C图乙2.观察图乙,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?91625⑵正方形A、B、C的
面积有什么关系?448SA+SB=SC图乙2.观察图乙,小方格
的边长为1.91625SA+SB=SC⑵正方形A、B、C的
面积有什么关系?448SA+SB=SC图甲abcabc3.猜想a、b、c 之间的关系?a2 +b2 =c2即:直角三角形两直角边的平方和等于斜边的平方命题1:如果直角三角形的两直角边长分别为a、b,斜边长为c,那么a2+b2=c2。abc你能证明这个命题是正确的命题吗?如图:已知四个全等的直角三角形的两直角边长分别为a和b,斜边长为c。利用这些直角三角形拼成一个大的正方形,来说明:
试一试(合作探究) ccc(a-b)2小正方形的面积怎样表示?(a+b)2=a2 + b2 + 2ab = c2+2ab可得: a2 + b2 = c2方法(二):对比两种方法,
你能得到什么?方法(一): 定理:经过证明被确认为正确的命题叫做定理。 这种证法是美国第二十任总统伽菲尔德发现的,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就称这一证法称为“总统”证法。
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”. 勾股定理如果直角三角形两直角边分别为a、b,斜边为c,那么即 直角三角形两直角边的平方和等于斜边的平方。勾股弦a2 + b2 = c2结论变形c2 = a2 + b2练习:
1、求下列图中字母所表示的正方形的面积=625=1442、求出下列直角三角形中未知边的长度解:由勾股定理得:x2 =36+64x2 =100x2=62+82∴ x=10∵ x2+52=132∴ x2=132-52x2 =169-25x2 =144∴ x=12∵ x > 0∵ x > 01.如图,这了测得湖两岸点A和点C间的距离,一个观测者在点B设立了一根标杆,使∠ACB=90°.测得AB=200m,BC=160m,根据测量结果求点A,C间的距离.ACB120m200m160m2、如图,受台风麦莎影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?小结:说说这节课你有什么收获?勾股小常识:勾股数
1、 a2+b2 =c2,满足(a,b,c)=1,a,b,c为基本勾股数.如:3、4、5 ; 5、12、 13;6、8、10;7、24、25……
2、如果a,b,c是一组勾股数,则ka、kb、kc(k为正整数)也是一组勾股数,如:6、8、10;9、12、15……
3、一组勾股数中必有一个数是5倍数。
再见!
