1.4 正切函数的性质和图象(学案)
文档属性
| 名称 | 1.4 正切函数的性质和图象(学案) |  | |
| 格式 | rar | ||
| 文件大小 | 105.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-11-24 13:12:00 | ||
图片预览


文档简介
曲靖市第二中学 第一章 三角函数 2010级高一数学备课组
1.4 正切函数的性质和图象
一、导学目标
1.理解并掌握作正切函数图象的方法;
2.掌握正切函数的性质及其应用;
3.能用正切函数的图象解最简三角不等式.
二、尝试练习
(一)探究正切函数的性质
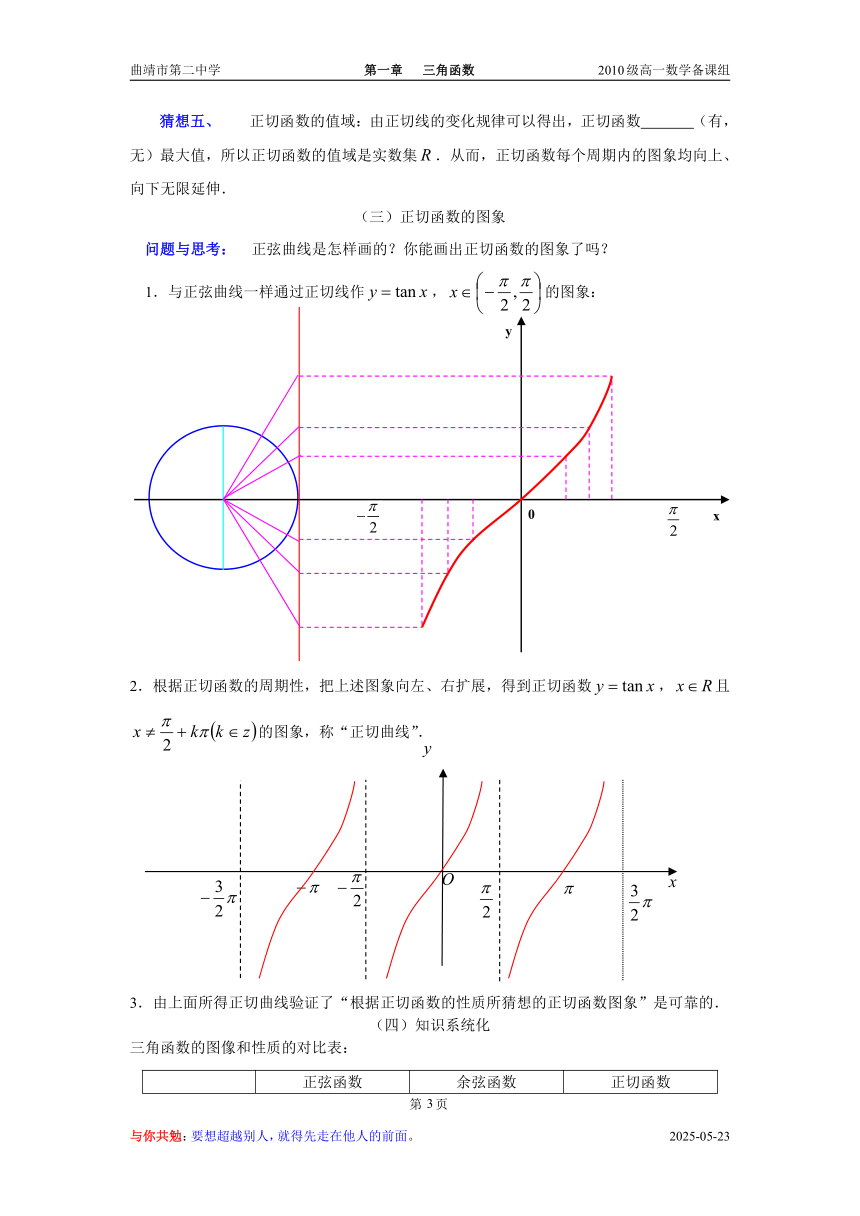
画出下列各角的正切线:
探究一、正切函数的定义域
当的终边在轴上时,点的横坐标等于,由正切函数的定义可知无意义;
当的终边在轴上时,过点的单位圆的切线平行于轴,它与的终边或其反向延长线不相交,正切线不存在.
所以,我们得到正切函数的定义域是:.
探究二、 正切函数的值域
由图(Ⅰ)可知,当大于且无限接近于时,正切线向轴的负方向无限延伸;由图(Ⅱ)可知,当小于且无限接近于时,正切线向轴的正方向无限延伸.因此,在内可以取任意实数,但没有最大值、最小值.因此,正切函数的值域是实数集.
探究三、正切函数的奇偶性
因为 且,所以正切函数()是 函数.于是可得:
正切函数()的图象应关于 对称.
探究四、正切函数的周期性
由诱导公式 且,可知函数()是 函数,且它的周期是 .
探究五、正切函数的单调性
由图(Ⅰ)、(Ⅱ)正切线的变化规律可以得出,正切函数在内是 函数,又由正切函数的周期性可知,正切函数在开区间内都是增函数.
【注意】正切函数在每一个开区间内均为增函数,但不能说正切函数在其定义域内是单调增函数.
(二)正切函数图象的猜想
根据正切函数的性质猜想正切函数的图象
猜想一、 正切函数的定义域: ),∴它的图象是由被互相平行的直线所隔开的无数多支曲线组成.
猜想二、 正切函数的周期性: ,∴的周期是 ,∴它的图象可由的图像向右、向左连续地平行移动(每次移动个单位长度)得到.
猜想三、 正切函数的奇偶性: ,∴是 函数,∴的图象应关于 对称.
猜想四、 正切函数的单调性:由正切线的变化规律可以得出,正切函数在内是 函数,所以正切函数在每个周期内的图象均呈上升趋势.
猜想五、 正切函数的值域:由正切线的变化规律可以得出,正切函数 (有,无)最大值,所以正切函数的值域是实数集.从而,正切函数每个周期内的图象均向上、向下无限延伸.
(三)正切函数的图象
问题与思考: 正弦曲线是怎样画的?你能画出正切函数的图象了吗?
1.与正弦曲线一样通过正切线作,的图象:
2.根据正切函数的周期性,把上述图象向左、右扩展,得到正切函数,且的图象,称“正切曲线”.
3.由上面所得正切曲线验证了“根据正切函数的性质所猜想的正切函数图象”是可靠的.
(四)知识系统化
三角函数的图像和性质的对比表:
正弦函数 余弦函数 正切函数
图象
定义域
值域
周期性
奇偶性
单调性
对称中心
(五)我也能行
1.函数y=tan(ax+)(a≠0)的最小正周期为 ( )
A ( http: / / wxc. ) B ( http: / / wxc. ) C ( http: / / wxc. ) D ( http: / / wxc. )
2.函数的定义域是 ( )
A ( http: / / wxc. ) B ( http: / / wxc. )
C ( http: / / wxc. ) D ( http: / / wxc. )
3. tan1、tan2、tan3的大小关系是 .
三、精点精评
例1 利用正切函数的单调性比较下列各组数中两个正切值的大小:
(1)与;(2)
例2 求函数的定义域、周期和单调区间.
例3 你能用图象求函数的定义域吗?
解:由得,利用图象知,所求定义域为,亦可利用单位圆求解.
四、直击高考
1.函数图象的对称中心是 ( http: / / wxc. )
2.(2007江西—文2)函数的最小正周期为 ( )
A ( http: / / wxc. ) B ( http: / / wxc. ) C ( http: / / wxc. ) D ( http: / / wxc. )
2.直线 y=a(a为常数)与正切曲线相交的相邻两点间的距离是 ( )
A ( http: / / wxc. ) B ( http: / / wxc. ) C ( http: / / wxc. ) D ( http: / / wxc. ) 与值无关
3.(2006全国I—文6)函数的单调增区间为 ( )
A ( http: / / wxc. ) B ( http: / / wxc. )
C ( http: / / wxc. ) D ( http: / / wxc. )
4.关于函数 , 有以下命题
①函数f(x)的周期是;
②函数f(x)的定义域是;
③y=f(x)是奇函数;
④y=f(x)的图象关于点 对称;
⑤y=f(x)的一个单调递增区间为;
其中,正确的是 .
5.作出函数y=|tanx|的图象,并观察函数的最小正周期.
五、课外阅读与欣赏
数形结合也未见得好
【案例】 在区间 范围内,函数y=tanx与函数y=sinx的图象交点的个数为( )
A. 1 B.2 C.3 D.4
〖解析〗 在同一坐标系中,作出y=sinx与y=tanx,在内的图象,很难做到精确,容易误认为3个交点.联想到不等式“sinx<x<tanx()”,故y=sinx与y=tanx,在内的图象无交点,又它们都是奇函数,从而y=sinx与y=tanx,在内的图象也无交点,所以在区间范围内,函数y=tanx与函数y=sinx的图象交点的个数为1个,即坐标原点(0,0).
〖注〗在同一坐标系中,函数y=sinx与y=tanx,在内的图象如下图所示:
我的感言
x
y
0
x
0
y
x
(Ⅰ)
的终边
的终边
(Ⅱ)
(Ⅲ)
的终边
(Ⅳ)
的终边
0
0
T
A
PAGE
6
第 页
与你共勉:要想超越别人,就得先走在他人的前面。 2010-11-23
1.4 正切函数的性质和图象
一、导学目标
1.理解并掌握作正切函数图象的方法;
2.掌握正切函数的性质及其应用;
3.能用正切函数的图象解最简三角不等式.
二、尝试练习
(一)探究正切函数的性质
画出下列各角的正切线:
探究一、正切函数的定义域
当的终边在轴上时,点的横坐标等于,由正切函数的定义可知无意义;
当的终边在轴上时,过点的单位圆的切线平行于轴,它与的终边或其反向延长线不相交,正切线不存在.
所以,我们得到正切函数的定义域是:.
探究二、 正切函数的值域
由图(Ⅰ)可知,当大于且无限接近于时,正切线向轴的负方向无限延伸;由图(Ⅱ)可知,当小于且无限接近于时,正切线向轴的正方向无限延伸.因此,在内可以取任意实数,但没有最大值、最小值.因此,正切函数的值域是实数集.
探究三、正切函数的奇偶性
因为 且,所以正切函数()是 函数.于是可得:
正切函数()的图象应关于 对称.
探究四、正切函数的周期性
由诱导公式 且,可知函数()是 函数,且它的周期是 .
探究五、正切函数的单调性
由图(Ⅰ)、(Ⅱ)正切线的变化规律可以得出,正切函数在内是 函数,又由正切函数的周期性可知,正切函数在开区间内都是增函数.
【注意】正切函数在每一个开区间内均为增函数,但不能说正切函数在其定义域内是单调增函数.
(二)正切函数图象的猜想
根据正切函数的性质猜想正切函数的图象
猜想一、 正切函数的定义域: ),∴它的图象是由被互相平行的直线所隔开的无数多支曲线组成.
猜想二、 正切函数的周期性: ,∴的周期是 ,∴它的图象可由的图像向右、向左连续地平行移动(每次移动个单位长度)得到.
猜想三、 正切函数的奇偶性: ,∴是 函数,∴的图象应关于 对称.
猜想四、 正切函数的单调性:由正切线的变化规律可以得出,正切函数在内是 函数,所以正切函数在每个周期内的图象均呈上升趋势.
猜想五、 正切函数的值域:由正切线的变化规律可以得出,正切函数 (有,无)最大值,所以正切函数的值域是实数集.从而,正切函数每个周期内的图象均向上、向下无限延伸.
(三)正切函数的图象
问题与思考: 正弦曲线是怎样画的?你能画出正切函数的图象了吗?
1.与正弦曲线一样通过正切线作,的图象:
2.根据正切函数的周期性,把上述图象向左、右扩展,得到正切函数,且的图象,称“正切曲线”.
3.由上面所得正切曲线验证了“根据正切函数的性质所猜想的正切函数图象”是可靠的.
(四)知识系统化
三角函数的图像和性质的对比表:
正弦函数 余弦函数 正切函数
图象
定义域
值域
周期性
奇偶性
单调性
对称中心
(五)我也能行
1.函数y=tan(ax+)(a≠0)的最小正周期为 ( )
A ( http: / / wxc. ) B ( http: / / wxc. ) C ( http: / / wxc. ) D ( http: / / wxc. )
2.函数的定义域是 ( )
A ( http: / / wxc. ) B ( http: / / wxc. )
C ( http: / / wxc. ) D ( http: / / wxc. )
3. tan1、tan2、tan3的大小关系是 .
三、精点精评
例1 利用正切函数的单调性比较下列各组数中两个正切值的大小:
(1)与;(2)
例2 求函数的定义域、周期和单调区间.
例3 你能用图象求函数的定义域吗?
解:由得,利用图象知,所求定义域为,亦可利用单位圆求解.
四、直击高考
1.函数图象的对称中心是 ( http: / / wxc. )
2.(2007江西—文2)函数的最小正周期为 ( )
A ( http: / / wxc. ) B ( http: / / wxc. ) C ( http: / / wxc. ) D ( http: / / wxc. )
2.直线 y=a(a为常数)与正切曲线相交的相邻两点间的距离是 ( )
A ( http: / / wxc. ) B ( http: / / wxc. ) C ( http: / / wxc. ) D ( http: / / wxc. ) 与值无关
3.(2006全国I—文6)函数的单调增区间为 ( )
A ( http: / / wxc. ) B ( http: / / wxc. )
C ( http: / / wxc. ) D ( http: / / wxc. )
4.关于函数 , 有以下命题
①函数f(x)的周期是;
②函数f(x)的定义域是;
③y=f(x)是奇函数;
④y=f(x)的图象关于点 对称;
⑤y=f(x)的一个单调递增区间为;
其中,正确的是 .
5.作出函数y=|tanx|的图象,并观察函数的最小正周期.
五、课外阅读与欣赏
数形结合也未见得好
【案例】 在区间 范围内,函数y=tanx与函数y=sinx的图象交点的个数为( )
A. 1 B.2 C.3 D.4
〖解析〗 在同一坐标系中,作出y=sinx与y=tanx,在内的图象,很难做到精确,容易误认为3个交点.联想到不等式“sinx<x<tanx()”,故y=sinx与y=tanx,在内的图象无交点,又它们都是奇函数,从而y=sinx与y=tanx,在内的图象也无交点,所以在区间范围内,函数y=tanx与函数y=sinx的图象交点的个数为1个,即坐标原点(0,0).
〖注〗在同一坐标系中,函数y=sinx与y=tanx,在内的图象如下图所示:
我的感言
x
y
0
x
0
y
x
(Ⅰ)
的终边
的终边
(Ⅱ)
(Ⅲ)
的终边
(Ⅳ)
的终边
0
0
T
A
PAGE
6
第 页
与你共勉:要想超越别人,就得先走在他人的前面。 2010-11-23
